Stats Tests

Front 1

In what situation would you use Spearman‘s rank correlation coefficient?

Back 1

To find out how strongly 2 variables are correlated (or whether there’s any correlation)

e.g. number of pesticide applications, index of diversity

Front 2

What does the student t-test actually do?

Back 2

Shows whether the difference in the mean of 2 data sets is significant

e.g. mean growth of unfertilised and fertilised plants

Front 3

When to use Unpaired student’s t-test?

Back 3

• 2 categorical groups - (e.g. treated and untreated)

• Groups made up of different individuals (independent data)

• interval data - data that is measured on a scale where each unit is the same size (e.g. length in cm)

Front 4

When would you use the Paired student’s t-test?

Back 4

• 2 categorical groups that include the same individuals (2 measurements taken from each individual, e.g. respiration rate before and after exercise)

• each measurement in one group paired with a measurement in other group

• both groups same size

Front 5

You do a student’s t-test and your t value is greater than the critical value (at your degrees of freedom and at a 0.05 probability level). What does this mean?

Back 5

• the difference between the means of the two groups is significant

• there is more than 95% probability that the difference between the two means is not due to chance (less than 5% that it is due to chance)

• reject the null hypothesis (there’s no difference in the means)

Front 6

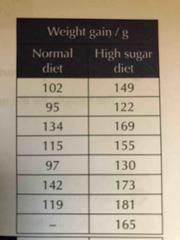
How would you work out the degrees of freedom of the above data?

Back 6

Unpaired student’s t-test

dF = (n1 + n2) - 2

dF = (7 + 8) - 2

dF = 13

Front 7

How would you work out the degrees of freedom (dF) for the above data?

Back 7

Paired student’s t-test

dF = n - 1

dF = 8 - 1

dF = 7

Front 8

You do a student’s t-test and your t value is greater than the critical value (at your degrees of freedom and a 0.01 probability level). What does this mean?

Back 8

• difference between the 2 means is significant

• more than 99% probability that the results are not due to chance

• reject the null hypothesis

Front 9

In what situation in a student’s t-test can you reject the null hypothesis?

Back 9

Your t-value ≥ critical value

Front 10

What is a critical value in a student’s t-test?

Back 10

The highlighted square - 3.499

Front 11

What does a significant result mean?

Back 11

Very unlikely to be due to chance

Front 12

Define - categorical data?

Back 12

Data that falls into distinct categories.

Front 13

What is a variable?

Back 13

A Factor in an experiment that does not have a fixed value - it can be controlled, changed or measured

Front 14

In a Chi-Squared test, when can you reject the null hypothesis?

Back 14

Your Chi-squared value ≥ the critical value

Front 15

Work our the degrees of freedom (dF) for a Chi-Squared test?

Back 15

Table with just one row/column.

dF = n - 1

dF = 4 - 3

dF = 3

Front 16

Work out the degrees of freedom (dF) for a Chi-Squared test?

Back 16

Table with just one row/column.

dF = n - 1

dF = 4 - 3

dF = 3

Front 17

Work out the degrees of freedom (dF) for a Chi-Squared test?

Back 17

Table with more than one row.

dF = (number of rows - 1) x (number of columns - 1)

dF = (2 - 1) x (2 - 1)

dF = 1

Front 18

What does Chi-Squared test actually do?

Back 18

Tests whether there is significant difference between observed and expected results

Front 19

Your chi-squared value is < the critical value (at your degrees of freedom and a probability level of 0.05). What does this mean?

Back 19

• the difference between the observed and expected results is not significant

• null hypothesis cannot be rejected

• “the results are not significantly different from what you might expect”

Front 20

When would you use a chi-squared test?

Back 20

• Categorical data (e.g. dark and light moth colour)

• The data is about frequencies

• the categories don’t have any particular order (like size)

• independent data - each person/plant only appears in your results once - results didn’t interfere with each other

Front 21

Work out the expected results in order to carry out a chi-squared test?

Back 21

Back (Definition)

Front 22

Calculation of the index of diversity of a population will give you a positive number ≥ 1.

What does an index of diversity of 1 mean?

Back 22

• All the organisms in the area are the same species

• There’s no diversity