![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
100 Cards in this Set
- Front
- Back
|
H5. Inleiding in de toetsende statistiek.
Samenvatting. Vaak komt het voor dat men met behulp van een schatter als het steekproefgemiddelde een populatieparameter wil schatten. Twee criteria voor een schatter zijn: |
a. zuiverheid;
b. efficiëntie. Het steekproefgemiddelde voldoet aan deze criteria. |
|
|
Het verband tussen steekproef en populatie wordt gelegd via het begrip
|
steekproevenverdeling.
|
|
|
De steekproevenverdeling van het gemiddelde bestaat uit
|
alle mogelijke waarden van steekproefgemiddelden bij steekproeven van een bepaalde grootte plus de bijbehorende kansen op die waarden.
|
|
|
De verwachte waarde van het gemiddelde is
μ¯χ = μ en de standaarddeviatie is: |
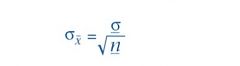
de standaarddeviatie is:
|
|
|
Wanneer de populatie normaal is verdeeld, dan is de steekproevenverdeling van het gemiddelde dat
|
ook.
|
|
|
De steekproevenverdeling is altijd bij benadering normaal verdeeld wanneer
|
n > 40.
We kunnen de kans op een bepaald steekproefgemiddelde of meer berekenen door deze normale verdeling om te zetten in de standaardnormale verdeling met behulp van de verwachte waarde en de standaarddeviatie van de steekproevenverdeling, dus door deze om te zetten in z-scores. |
|
|
We kunnen de kans op een bepaald steekproefgemiddelde of meer berekenen door deze normale verdeling om te zetten in de
|
standaardnormale verdeling met behulp van de verwachte waarde en de standaarddeviatie van de steekproevenverdeling, dus door deze om te zetten in z-scores.
|
|
|
Variabelen in de onderzoekshypothese moeten worden geoperationaliseerd en vervolgens moeten de hypothesen worden omgezet in een
|
statistische hypothese ofwel een alternatieve hypothese en deze laatste wordt afgezet tegen de nulhypothese.
|
|
|
Onder aanname van de juistheid van de nulhypothese wordt de kans op een bepaald steekproefgemiddelde of groter berekend. Wanneer deze kans kleiner is dan of gelijk aan α, wordt de nulhypothese
|
verworpen.
|
|
|
Een tweede manier is het werken met kritieke zones. Hierbij gaan we na of de waarde van de toetsingsgrootheid in de kritieke zone valt. Is dit het geval dan wordt de Ho verworpen.
Het is hierbij mogelijk om twee soorten fouten te maken: |
1 fout van de eerste soort: het ten onrechte verwerpen van Ho met
kans α. 2 fout van de tweede soort: het ten onrechte niet verwerpen van de Ho met kans β. |
|
|
Al naar gelang de onderzoekshypothesen kunnen toetsen
rechtseenzijdig, linkseenzijdig of tweezijdig worden uitgevoerd: |

|
|
|
De keuze tussen eenzijdig of tweezijdig toetsen wordt bepaald door
|
het antwoord op de vraag of er in de hypothese een verwachte richting van het verband wordt aangegeven.
|
|
|
Behalve het toetsen van hypothesen omtrent het gemiddelde kan ook een betrouwbaarheidsinterval van het populatiegemiddelde worden berekend.
Dit geeft met een bepaald percentage zekerheid de grenzen aan waarbinnen .... |
het populatiegemiddelde zich bevindt.
Het interval bevat alle waarden van het populatiegemiddelde die bij tweezijdige toetsing niet zouden worden verworpen. |
|
|
Het interval bevat alle waarden van ....
|
het populatiegemiddelde die bij tweezijdige toetsing niet zouden worden verworpen.
|
|
|
Als je uitspraken over populaties wil doen, hangt het nut van onderzoek via steekproeven af van:
|
de vraag of de steekproefresultaten kunnen worden gegeneraliseerd naar die populaties.
|
|
|
Door de steekproefverdeling, de berekende steekproefgrootheden kunnen we:
|
Uitspraken doen over de overeenkomstige populatieparameters.
|
|
|
We schatten de waarden van de populatieparameters op grond van de
|
steekproefgegevens.
|
|
|
De toetsende statistiek kent 2 basis procedures om op grond van steekproefgrootheden tot uitspraken over populatieparameters te komen:
|
1. De toetsing van Hypothesen.
2. De bepaling van betrouwbaarheidsintervallen. |
|
|
1. De toetsing van Hypothesen.
2. De bepaling van betrouwbaarheidsintervallen. |
1. De toetsing van Hypothesen.
Is een bepaalde van tevoren opgestelde uitspraak over de populatie houdbaar gezien het resultaat in de steekproef? 2. De bepaling van betrouwbaarheidsintervallen. Binnen welke grenzen ligt de waarde van de populatieparameter? |
|
|
Schatten.
Het berekenen van steekproefgrootheden als het gemiddelde, de standaardafwijking, de regressie- en de correlatiecoëfficiënt heeft in de regel weinig zin als: |
We niet in staat zijn om op basis van deze gegevens uitspraken te doen over de populatie.
|
|
|
Het opstellen van kansverdelingen die een populatie beschrijven heeft nauwelijks betekenis als
|
we de parameters (zoals de verwachtte waarde en de standaardafwijking) van die verdelingen niet kunnen schatten op basis van steekproefgegevens.
|
|
|
Er moet dus een verbinding gelegd worden tussen de steekproefgrootheden enerzijds en
|
De populatie parameters anderzijds.
We willen iets kunnen zeggen over de een op basis van de ander. |
|
|
Wat is een 'schatter'?
|
een 'schatter' is de steekproefgrootheid waarmee we een verwachtte waarde willen schatten.
Denk aan het gemiddelde van een steekproef ten aanzien van het gemiddelde van een populatie. Het gemiddelde is dan de schatter. |
|
|
Is het gemiddelde een goede 'schatter'?
Er moeten 2 criteria zijn: |
A. Zuiverheid
B. Efficiëntie |
|
|
Is het gemiddelde een goede 'schatter'?
Er moeten 2 criteria zijn: A. Zuiverheid B. Efficiëntie |
A. Zuiverheid
De schatter moet zuiver (unbiased) zijn. Een schatter mag gemiddeld over alle mogelijke steekproeven geen systematische afwijkingen vertonen ten opzichte van de te schatten populatiegrootheid. Een schatter mag dus niet systematisch te groot zijn of te klein. B. Efficiëntie De schattingen moeten ook bij kleine steekproeven al in de buurt van de echte populatiewaarde liggen. |
|
|
A. Zuiverheid
|
De schatter moet zuiver (unbiased) zijn. Een schatter mag gemiddeld over alle mogelijke steekproeven geen systematische afwijkingen vertonen ten opzichte van de te schatten populatiegrootheid. Een schatter mag dus niet systematisch te groot zijn of te klein.
|
|
|
B. Efficiëntie
|
De schattingen moeten ook bij kleine steekproeven al in de buurt van de echte populatiewaarde liggen.
|
|
|
Wat is een steelproef verdeling van het gemiddelde?
|
Wanneer je alle mogelijke steekproeven neemt uit een populatie heb je een variabele met een eigen kansverdeling. Immers, van steekproef tot steekproef zal het gemiddelde verschillen.
De steekproef verdeling van het gemiddelde bestaat dus uit alle mogelijke waarden van de steekproefgemiddelden. plus de kansen op die waarden. |
|
|
Omdat het een kansverdeling is heeft het dan ook
|
een gemiddelde verwachtte waarde μ en een variantie .
De verwachtte waarde van de steekproefverdeling van het gemiddelde μx is gelijk aan de verwachtte waarde van de populatie μ. |
|
|
Wanneer we uit een populatie alle mogelijke steekproeven trekken van een bepaalde grootte (n) en daar steeds het gemiddelde X van bepalen heet de kansverdeling van deze gemiddelden:
|
De steekproefverdeling van het gemiddelde
|
|
|
De verwachtte waarde van de steekproefverdeling van het gemiddelde is gelijk aan dat van
|
De populatie
|
|
|
De standaardfout van het gemiddelde
Als we van de steekproef verdeling van het gemiddelde de standaardafwijking bepalen, is dat het zelfde als wanneer we van alle mogelijke steelproefgemiddelden de standaardafwijking zouden berekenen. |
Om deze standaardafwijking te berekenen trekken we van alle verwachtte waarden het gemiddelde μ af.
We berekenen dus eigenlijk de standaardafwijking van de fouten die we met onze steekproefgemiddelden hebben gemaakt. Daarom heet deze standaardafwijking ook wel de standaardfout van het gemiddelde genoemd. |
|
|
Zuivere schatter en onzuivere schatters
Zuivere schatters zijn |
-Het steekproef gemiddelde
-Relatieve frequentie de steekproef -regressiecoëfficiënt -Het gemiddelde. Dat is beter dan de mediaan. De standaardfout van het gemiddelde is kleiner dan die van de mediaan. |
|
|
Onzuivere schatters zijn
|
-De standaardafwijking
-De variantie berekend met n in de noemer in plaats van n-1 |
|
|
Steekproef verdeling bij een normaal verdeelde populatie
Als de populatie waaruit de steekproeven van een bepaalde grootte worden getrokken normaal verdeeld is, dan is de steekproefverdeling van het gemiddelde |
ook normaal verdeeld.
|
|
|
Steekproef verdeling bij een iet normaal verdeelde populatie
Als een populatie niet normaal verdeeld is, maar de steekproeven zijn groot, bijvoorbeeld n > 30 dan kan men aantonen dat de steekproef verdeling van het gemiddelde bij benadering normaal verdeeld is met een gemiddelde van μx = μ en eenstandaardafwijking σx = σ/√n, mits... |
de standaardafwijking σ bekend is.
|
|
|
Wanneer de steekproef honderd of meer is, dan hoeft zelfs de σ niet meer bekend te zijn en mag in plaats van σ de
|
standaardafwijking van de steekproef gebruikt worden
|
|
|
Tussen de 30 en de 100 wordt welke verdeling gebruikt?
|
De t-verdeling
|
|
|
We kunnen op grond van het gemiddelde van steekproef X en de steekproef grootte n conclusies trekken over het populatie gemiddelde μ.
Ook kunnen we bij een specifieke waarde van μ de kans berekenen p een bepald steekproef gemiddelde of groter. kortom we kunnen de overschrijdingskans berekenen. Wel moeten we het steekproefgemiddelde eerst omzetten naar een |
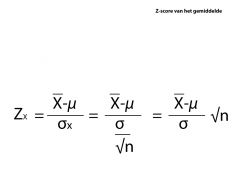
Z-score.
De overschrijdingskans van de Z score kan je opzoeken in een tabel |
|
|
We weten nu hoe je overschrijdingskansen van gemiddelden van kunnen uitrekenen. Hiermee kunnen we ..... toetsen
|
hypothesen toetsen
|
|
|
Onderzoek (toetsend onderzoek) heeft betrekking op
|
een theorie waarvan men de juistheid wil nagaan
|
|
|
5.3 Toetsen van hypothesen
Nu we weten hoe we bij gemiddelden van steekproeven overschrijdingskansen kunnen berekenen, kunnen we deze bevindingen gebruiken bij |
het toetsen van hypothesen.
Voordat we tot het daadwerkelijke toetsen overgaan eerst iets over het begrip 'onderzoekshypothese'. Onderzoek (althans het toetsend onderzoek) heeft betrekking op een theorie waarvan men de juistheid wil nagaan. Het verschil tussen theorie en hypothese is niet altijd even duidelijk, maar een theorie is in principe in algemene (meer abstracte) termen geformuleerd. Uit een theorie kunnen vaak één of meer onderzoekshypothesen worden afgeleid. Deze hypothesen zijn in meer specifieke termen geformuleerd en beslaan doorgaans een beperkter terrein dan de achterliggende theorie. |
|
|
Voordat we tot het daadwerkelijke toetsen overgaan eerst iets over het begrip 'onderzoekshypothese'.
Onderzoek (althans het toetsend onderzoek) heeft betrekking op |
een theorie waarvan men de juistheid wil nagaan.
Het verschil tussen theorie en hypothese is niet altijd even duidelijk, maar een theorie is in principe in algemene (meer abstracte) termen geformuleerd. |
|
|
Uit een theorie kunnen vaak
|
één of meer onderzoekshypothesen worden afgeleid.
Deze hypothesen zijn in meer specifieke termen geformuleerd en beslaan doorgaans een beperkter terrein dan de achterliggende theorie. |
|
|
Voorbeelden van hypothesen
|
a Intelligentie en schoolvorderingen zijn positief gecorreleerd.
b Schooluitval is hoger voor kinderen uit gezinnen met een lage sociaaleconomische status dan voor kinderen uit gezinnen met een hoge sociaal-economische status. c De snelheid waarmee een bepaalde taak wordt geleerd, is recht evenredig aan de hoeveelheid training. d Autoritaire leraren geven effectiever les dan Laissez-faire-leraren. e De globale methode om kinderen te leren lezen (A) geeft betere resultaten dan de analytische methode (B) |
|
|
Begrippen in de hypothese operationaliseren
Onderzoekshypothesen, zoals hiervoor geformuleerd, zijn nog niet direct |
toetsbaar.
Eerst moet nog worden aangegeven wat onder de gebruikte begrippen wordt verstaan en hoe zij moeten worden gemeten: de begrippen moeten nog worden geoperationaliseerd. Bij de hypothese 'Intelligentie en schoolvorderingen zijn positief gecorreleerd' moet dus worden aangegeven hoe 'intelligentie' en 'schoolvorderingen' worden gemeten: welke intelligentietest gebruikt gaat worden en of we schoolvorderingen gaan meten met behulp van schoolcijfers of met een schoolvorderingentoets. Dit leidt tot een geherformuleerde hypothese in operationeel gedefinieerde begrippen. |
|
|
Eerst moet nog worden aangegeven wat onder de gebruikte begrippen wordt verstaan en hoe zij moeten worden gemeten:
de begrippen moeten nog worden |
geoperationaliseerd.
Bij de hypothese 'Intelligentie en schoolvorderingen zijn positief gecorreleerd' moet dus worden aangegeven hoe 'intelligentie' en 'schoolvorderingen' worden gemeten: welke intelligentietest gebruikt gaat worden en of we schoolvorderingen gaan meten met behulp van schoolcijfers of met een schoolvorderingentoets. Dit leidt tot een geherformuleerde hypothese in operationeel gedefinieerde begrippen. |
|
|
Geherformuleerde hypothese omzetten in een statistische hypothese
Uit de geherformuleerde hypothese met geoperationaliseerde begrippen kan wat worden afgeleid? |
namelijk een statistische hypothese worden afgeleid.
Een onderzoekshypothese wordt dus meestal getoetst met behulp van een statistische hypothese. Bij de onderzoekshypothese 'Intelligentie en schoolvorderingen zijn positief gecorreleerd' zou de statistische hypothese kunnen zijn: 'In de populatie is de correlatiecoëfficiënt tussen de variabelen IQ en Schoolsucces positief'. |
|
|
Bij de onderzoekshypothese 'Intelligentie en schoolvorderingen zijn positief gecorreleerd' zou de statistische hypothese kunnen zijn:
|
'In de populatie is de correlatiecoëfficiënt tussen de variabelen IQ en Schoolsucces positief'.
|
|
|
Statistische hypothese eigens tegen afzetten
We toetsen bijvoorbeeld de bewering μA > μB niet direct, maar we toetsen de statistische hypothese tegen een andere hypothese: |
de nulhypothese.
De nulhypothese (aangeduid met H0) is een statistische bewering die in essentie zegt dat er géén relatie is tussen de variabelen in het onderzoeksprobleem (vandaar de naam nu/hypothese), of dat de relatie zelfs tegengesteld is aan die in de statistische hypothese. |
|
|
De nulhypothese (aangeduid met H0) is een statistische bewering die in essentie zegt dat
|
er géén relatie is tussen de variabelen in het onderzoeksprobleem (vandaar de naam nulhypothese), of dat de relatie zelfs tegengesteld is aan die in de statistische hypothese.
|
|
|
De nulhypothese beweert dus in statistische termen dat μA = μB = 0 ofwel ,μA - μB =0 (of meer extreem dat μA ≤ μB ofwel μA - μB ≤ 0.
We trachten nu via een onderzoek en/of experiment aan te tonen dat de nulhypothese H0 onjuist is, om vervolgens |
als alternatief de andere hypothese te accepteren.
|
|
|
We leggen de toetsing van een hypothese uit via een voorbeeld.
De onderzoekshypothese is dat kinderen van ongeveer elf jaar die een cursus 'syllogismen oplossen' hebben gevolgd, daardoor beter gaan redeneren. De cursus 'syllogismen oplossen' bestaat uit een aantal bijeenkomsten waarin de kinderen klassikaal leren of bepaalde syllogismen goed of fout zijn. Om 'redeneren' te meten, wordt een redeneertest gebruikt die redeneringen bevat waarvan de kinderen moeten aangeven welke fout een redenering bevat. Van deze test is gegeven dat de scores normaal verdeeld zijn met een gemiddelde van 50 en een standaarddeviatie van 10, dus μ = 50 en u = 10. Als de kinderen beter hebben leren redeneren dan kinderen in het algemeen, dan moet het gemiddelde van de kinderen die zo'n cursus hebben gevolgd groter zijn dan 50. We noemen dit de alternatieve hypothese H 1 . De alternatieve hypothese (of: statistische hypothese) is dus dat kinderen die de cursus gevolgd hebben, hoger scoren op de redeneertest dan kinderen in het algemeen. Kort en bondig samengevat: |
H1:μ > 50.
|
|
|
Nulhypothese
De nulhypothese stelt dat er geen verschil is of dat het verschil zelfs tegengesteld is aan de alternatieve hypothese. Dus: H0: μ ≤ 50. De H0 bestrijkt het gebied dat niet door de H1 wordt bestreken. De H0 bevat altijd een = -teken, dus ook een ≤ of een ≥ -teken zijn geoorloofd bij een H0. De alternatieve hypothese bevat nooit een = -teken. We trekken een aselecte steekproef van 64 kinderen. Na het volgen van de cursus nemen we bij deze steekproef de redeneertest af en bepalen het gemiddelde en de standaardafwijking. We vinden een gemiddelde van 53 en een standaarddeviatie van 7. Dus voor de steekproef geldt: X = 53; sx = 7; n = 64. Het gemiddelde van de steekproef is groter dan 50. Kunnen we nu de nulhypothese verwerpen? |
Nee, dat kan niet zonder meer, want het is
mogelijk dat het gemiddelde van de steekproef door toeval 53 of nog hoger is. Om de invloed van dit toeval vast te kunnen stellen, nemen we even aan dat de H0 juist is en er dus geen effect is. We veronderstellen met andere woorden dat de waarde van μ gelijk is aan 50. Hoe toevallig een gemiddelde van 53 of meer in dat geval is, komt dan neer op de volgende vraag: 'Hoe groot is de kans op een steekproefgemiddelde van 53 of meer in een steekproef van n = 64 uit een populatie met een gemiddelde van μ = 50 en een standaardafwijking van μ = 10?' Met andere woorden, we vragen de rechter overschrijdingskans van X= 53 als p = 50. |
|
|
Met andere woorden, we vragen de rechter overschrijdingskans van X= 53 als p = 50.
|
1 Als die kans groot is, is het verschil tussen μ = 50 en X = 53 waarschijnlijk aan toeval te wijten. Het is dan heel waarschijnlijk dat een steekproef wordt getrokken met een gemiddelde van 53 of meer als het populatiegemiddelde 50 is.
De 'kinderen met cursus' (in de steekproef) verschillen dan niet aantoonbaar van de 'kinderen zonder cursus' en er kan geen effect van de cursus worden geconstateerd. 2 Maar als die kans heel klein is, dan is het erg onwaarschijnlijk dat het verschil op basis van toeval tot stand is gekomen. Het ligt dan meer voor de hand om aan te nemen dat de kinderen in de steekproef inderdaad verschillen van de kinderen in het algemeen en dat de cursus wél effect heeft gehad. In dat geval verwerpen we de nulhypothese ten gunste van de alternatieve hypothese en concluderen dat μ > 50. |
|
|
Als vertaling van het begrip 'heel kleine kans' wordt in de praktijk vaak de waarde van 0,05, of 0,01 gehanteerd.
Deze grenswaarde heet het |
signiflcantieniveau
en wordt aangegeven met de Griekse letter α (alfa). Een andere naam is: onbetrouwbaarheidsdrempel. Is de gevonden overschrijheidsdrempel kleiner dan of gelijk aan α, dan verwerpen we de nulhypothese. |
|
|
Beslissingsregel
De nulhypothese wordt verworpen als de berekende overschrijdingskans |
kleiner is of gelijk aan de vooraf gekozen waarde van de kans α.
In ons voorbeeld is de berekende overschrijdingskans (0,0082) kleiner dan 0,05 en dus verwerpen we de nulhypothese. Bijgevolg concluderen we dat het gemiddelde van kinderen die een cursus 'syllogismen oplossen' hebben gevolgd, hoger is dan 50. Aangetoond? Het is wellicht goed om te benadrukken dat we slechts hebben aangetoond dat het gemiddelde van de kinderen die een cursus 'syllogismen oplossen' hebben gevolgd, hoger is dan 50. Of dat hogere gemiddelde ook daadwerkelijk is veroorzaakt door de cursus, hangt af van de onderzoeksopzet en de mate waarin deze onderzoeksopzet alternatieve verklaringen toelaat (zie Hart e.a. 1998; Hoyle a.o. 2002). |
|
|
Aangetoond?
Het is wellicht goed om te benadrukken dat we slechts hebben aangetoond dat het gemiddelde van de kinderen die een cursus 'syllogismen oplossen' hebben gevolgd, hoger is dan 50. Of dat hogere gemiddelde ook daadwerkelijk is veroorzaakt door de cursus, hangt af van |
de onderzoeksopzet en de mate waarin deze onderzoeksopzet alternatieve verklaringen toelaat (zie Hart e.a. 1998; Hoyle a.o. 2002).
|
|
|
5.4 Mogelijke fouten
We hebben hiervóór gekozen voor een kans, een significantieniveau, van 0,05 (α = 0,05) . De grootte van deze ais een keuze die afhangt van het risico dat we accepteren om een fout te maken. Want een significantieniveau van 0,05 betekent in feite dat als we besluiten om de H0 te verwerpen, er 5% kans is dat de beslissing fout is en de nulhypothese ten onrechte wordt verworpen. |
Dit heet een fout van de eerste soort.
Wanneer we een kans van 0,05, dus α = 0,05, een te groot risico vinden, dan kunnen we een kleinere alfa kiezen, bijvoorbeeld α= 0,01. Wanneer α~0,01 wordt genomen, is er nog slechts een kans van 1 op honderd dat de nulhypothese wordt verworpen terwijl deze in feite juist is. |
|
|
Wanneer we een kans van 0,05, dus α = 0,05, een te groot risico vinden, dan kunnen we een kleinere alfa kiezen, bijvoorbeeld α= 0,01. Wanneer α~0,01 wordt genomen, is er nog slechts een kans van 1 op honderd dat de nulhypothese wordt verworpen terwijl deze in feite juist is.
Als we fouten willen vermijden, waarom nemen we dan niet altijd een zo klein mogelijke alfa, bijvoorbeeld α= 0,0000001 of iets dergelijks? |
Er is een goede reden om dat niet te doen. Het is namelijk óók mogelijk dat de H0 niet juist is en we hem tóch niet verwerpen.
Deze fout, waarbij we de H0 ten onrechte niet verwerpen, noemen we de fout van de tweede soort en de kans op deze fout duiden we aan met de griekse letter β (bèta) . Met andere woorden, er zijn bij het nemen van beslissingen omtrent de nulhypothese vier mogelijkheden... |
|
|
Deze fout, waarbij we de H0 ten onrechte niet verwerpen, noemen we de fout van de tweede soort en de kans op deze fout duiden we aan met de griekse letter β (bèta) .
Met andere woorden, er zijn bij het nemen van beslissingen omtrent de nulhypothese vier mogelijkheden: |
a Fout van de eerste soort
De H0 wordt verworpen, maar de H0 is juist; kans α. (α = kans op ten onrechte verwerpen van de H0) b Juiste beslissing De H0 wordt niet verworpen en de H0 is juist; kans 1 - α. c Juiste beslissing De H0 wordt verworpen en de H0 is onjuist; kans 1 - β. d Fout van de tweede soort De H0 wordt niet verworpen, maar de H0 is onjuist; kans β. (β = kans op het ten onrechte niet verwerpen van de H0). |
|
|
Helaas is het zo dat de foutenkans β groter wordt als we α kleiner nemen.
We kunnen dus wel een heel kleine alfa kiezen, maar |
dan wordt de kans bèta om een fout van de tweede soort te maken onaanvaardbaar groot.
Dat betekent dat de kans dan erg groot is dat er bijvoorbeeld in de populatie wél een verband aanwezig is, maar dat het niet lukt om dat met behulp van een steekproef aan te tonen, tenzij we een heel grote steekproef nemen. Met andere woorden: het onderscheidingsvermogen van de toets is dan erg klein (gelijk aan 1 - β. |
|
|
Hoe groter β wordt,
|
hoe kleiner dus het onderscheidingsvermogen (= power) van de toets (zie hoofdstuk 10, waar we het onderscheidingsvermogen van een statistische
toets behandelen). Het is alleen mogelijk om de foutenkans β bij een bepaalde alfa kleiner te krijgen door een grotere steekproef te nemen. In de sociale wetenschappen is het meest gebruikelijke significantieniveau a = 0,05. Wanneer onderzoekers 'streng' willen toetsen, kiezen ze meestal voor α =0,01. |
|
|
Linkseenzijdig toetsen
Veronderstel dat we aan een aselecte steekproef van 36 kinderen extra spellingslessen geven, waarvan we verwachten dat kinderen hierdoor minder spelfouten maken. We meten dit met behulp van een landelijk geijkte spellingstest waarvan de scores normaal verdeeld zijn met μ= 70 en σ = 15. Dus de nulhypothese is hier H0: μ ≥ 70 en de alternatieve hypothese is H1: μ < 70. We zijn hier dus alleen geïnteresseerd in de vraag of het steekproefgemiddelde voldoende kleiner is dan 70. We noemen dit daarom |
een grotere steekproef te nemen. In de sociale wetenschappen
is het meest gebruikelijke significantieniveau α = 0,05. Wanneer onderzoekers 'streng' willen toetsen, kiezen ze meestal voor α = 0,01. |
|
|
Tweezijdig toetsen
Neem aan dat een vragenlijst naar sociale vaardigheden landelijk is geijkt. De scores zijn normaal verdeeld met een gemiddelde van 100 en een standaarddeviatie van 20, dus p.= 100 en σ = 20. We willen weten of de sociale vaardigheid van studenten die een exacte studie volgen, afwijkt van de landelijke norm p. = 100. De nulhypothese zegt dat er géén afwijking is. De alternatieve hypothese beweert dat er wél een afwijking is, maar dat niet aan te geven valt in welke richting de gemiddelde sociale vaardigheidsscore zal afwijken. Dus: H0: μ = 100 en H1: μ ≠ 100. Dit heet: |
rechtseenzijdig toetsen.
Wanneer de rechter overschrijdingskans van de z-waarde van het gemiddelde kleiner is dan het gekozen significantieniveau α, verwerpen we de 0-hypothese. |
|
|
5.5 Hypothesen met en zonder richting
Rechtseenzijdig toetsen Stel, de nulpothese is H0: μ ≤ 50 en de alternatieve hypothese was H1: μ > 50. We zijn dus alleen geïnteresseerd in de vraag of het steekproefgemiddelde voldoende groter is dan 50. We noemen dit |
rechtseenzijdig toetsen.
Wanneer de rechter overschrijdingskans van de z-waarde van het gemiddelde kleiner is dan het gekozen significantieniveau α, verwerpen we de nulhypothese |
|
|
Linkseenzijdig toetsen
Veronderstel dat we aan een aselecte steekproef van 36 kinderen extra spellingslessen geven, waarvan we verwachten dat kinderen hierdoor minder spelfouten maken. We meten dit met behulp van een landelijk geijkte spellingstest waarvan de scores normaal verdeeld zijn met μ= 70 en σ= 15. Dus de nulhypothese is hier H0: μ~ 70 en de alternatieve hypothese is H1: μ < 70. We zijn hier dus alleen geïnteresseerd in de vraag Unkseenzijdig of het steekproefgemiddelde voldoende kleiner is dan 70. We noemen dit daarom |
linkseenzijdig toetsen.
|
|
|
Tweezijdig toetsen
Neem aan dat een vragenlijst naar sociale vaardigheden landelijk is geijkt. De scores zijn normaal verdeeld met een gemiddelde van 100 en een standaarddeviatie van 20, dus p.= 100 en σ = 20. We willen weten of de sociale vaardigheid van studenten die een exacte studie volgen, afwijkt van de landelijke norm p. = 100. De nulhypothese zegt dat er géén afwijking is. De alternatieve hypothese beweert dat er wél een afwijking is, maar dat niet aan te geven valt in welke richting de gemiddelde sociale vaardigheidsscore zal afwijken. Dus: H0: μ = 100 en Hl: μ ≠e 100. Dit heet |
tweezijdig toetsen,
omdat we nagaan of het steekproefgemiddelde voldoende ver afwijkt van μ = 100; of het dus duidelijk boven óf duidelijk beneden μ= 100 ligt, zonder daarbij een richting te specificeren. Bij een gekozen waarde van α (zeg 0,05) betekent dit dat we de H0 naar twee kanten kunnen verwerpen. één kant waarbij het steekproefgemiddelde te ver van μ = 100 afwijkt omdat het te klein is, of de andere kant waarbij het steekproefgemiddê1de te ver van μ = 100 afwijkt omdat het te groot is. |
|
|
Doordat we de nulhypothese op twee manieren kunnen verwerpen bestaat de kans op een fout van de eerste soort ook uit twee stukken:
|
één kant waarbij het steekproefgemiddelde
te ver van μ = 100 afwijkt omdat het te klein is, of de andere kant waarbij het steekproefgemiddelde te ver van μ = 100 afwijkt omdat het te groot is. |
|
|
Doordat we de nulhypothese op twee manieren kunnen verwerpen bij tweezijdigtoetsen, bestaat de kans op een fout van de eerste soort ook
|
uit twee stukken: de kans op de fout waarbij μ = 100, maar het steekproefgemiddelde
toevallig te laag uitvalt (en we daarom ten onrechte verwerpen), plus de kans op de fout waarbij μ = 100 en het steekproefgemiddelde toevallig te hoog uitvalt (en we daarom ten onrechte verwerpen). Beide kansen wegen even zwaar en zijn samen gelijk aan α. We moeten dus een tweezijdige overschrijdingskans uitrekenen we verwerpen H0 als de tweezijdige overschrijdingskans kleiner is dan α. |
|
|
5.6 Kritieke waarde van een toetsingsgrootheid en het verwerpingsgebied
In het voorgaande hebben we steeds de overschijdingskans van het steekproefgemiddelde bepaald en vastgesteld of deze gelijk aan of kleiner was dan het gekozen significantieniveau α om de H0 te kunnen verwerpen. We kunnen dezelfde conclusie echter ook op een iets andere manier bereiken. Aan de hand van het significantieniveau grenzen we een gebied af waarin we de nulhypothese verwerpen. Komt de standaardscore van het steekproefgemiddelde zx. in dit gebied terecht, dan |
verwerpen we de H0.
Het voordeel van deze toetsingsprocedure is, dat we niet steeds de overschrijdingskans van het gemiddelde hoeven te bepalen, maar dat we met enkele grenswaarden kunnen volstaan. Als we naderhand met andere verdelingen dan de normale verdeling toetsen, hoeven daarom niet zulke uitgebreide tabellen te hebben. Tabellen met grenswaarden die bij een bepaald significantieniveau behoren, voldoen reeds . |
|
|
Het voordeel van deze toetsingsprocedure is, dat
|
we niet steeds de overschrijdingskans van het gemiddelde hoeven te bepalen, maar dat we met enkele grenswaarden kunnen volstaan.
Als we naderhand met andere verdelingen dan de normale verdeling toetsen, hoeven daarom niet zulke uitgebreide tabellen te hebben. Tabellen met grenswaarden die bij een bepaald significantieniveau behoren, voldoen reeds . |
|
|
Ook bij deze bespreking gaan we weer uit van de standaardscore van het steekproefgemiddelde zx..
Omdat we in dit geval met de grootheid zx. toetsen, heet deze de toetsingsgrootheid. De toetsingsgrootheid waarmee we hier werken is dus: |
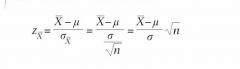
|
|

|
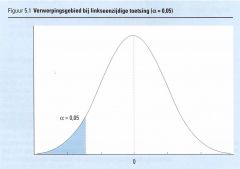
Als α = 0,05 wordt de H0 verworpen wanneer zx ≤ -1,64 (de z-waarde die we in de tabel voor de standaardnormale verdeling vinden bij α = 0,05).
Voor waarden van kleiner dan zx -1,64, bijvoorbeeld -2,28, geldt dat de linker overschrijdingskans kleiner is dan α = 0,05. Dergelijke waarden liggen immers nog verder af van het gemiddelde 0 van de standaardnormale verdeling dan zx = -1,64 en dus is de linker overschrijdingskans van dergelijke waarden kleiner. Of we nu nagaan of PL(zx) ≤ α of dat we nagaan zx ≤ -1,64 is dus volstrekt identiek, mits we de z-waarde nemen die bij de α behoort. |
|
|
Alle waarden kleiner of gelijk aan -1,64 heten tezamen: de (linker) kritieke zone of het verwerpingsgebied van de H0 bij linkseenzijdige toetsing.
Komt de waarde van zx terecht in dit gebied, dan verwerpen we de H0 . De grenswaarde z = - 1,64 heet ook wel de kritieke waarde van de toetsingsgrootheid Zx. Als de toetsingsgrootheid zx kleiner is dan de kritieke waarde en dus in het verwerpingsgebied terechtkomt, verwerpen we |
de nulhypothese. Het populatiegemiddelde is dan significant kleiner dan de waarde μ 0 bij een gegeven waarde van α.
|
|
|
S.7 Een- óf tweezijdig toetsen
De keuze voor een eenzijdige toets wordt bepaald door |
de formulering van de alternatieve hypothese en deze formulering hangt weer af van de onderzoekshypothese.
Als in de onderzoekshypothese duidelijk staat dat onder conditie A hoger wordt gescoord dan onder conditie B, dan is er sprake van een duidelijk verwachte richting van het verschil en moet er dus eenzijdig worden getoetst, hier dus rechtseenzijdig. |
|
|
Als in de onderzoekshypothese duidelijk staat dat onder conditie A hoger wordt gescoord dan onder conditie B, dan is er sprake van
|
een duidelijk verwachte richting van het verschil en moet er dus eenzijdig worden getoetst, hier dus rechtseenzijdig.
Het verschil tussen rechtseenzijdig en linkseenzijdig hangt daarbij soms af van de conditie die als eerste wordt genoemd. Veronderstel dat de onderzoekshypothese was geweest: onder conditie B wordt lager gescoord dan onder conditie A. In dat geval zou er linkseenzijdig zijn getoetst. |
|
|
Het verschil tussen rechtseenzijdig en linkseenzijdig hangt daarbij soms af van
|
de conditie die als eerste wordt genoemd.
Veronderstel dat de onderzoekshypothese was geweest: onder conditie B wordt lager gescoord dan onder conditie A. In dat geval zou er linkseenzijdig zijn getoetst. Dus als er een duidelijke richting in de onderzoekshypothese wordt geformuleerd, wordt er eenzijdig getoetst. Wordt er in de onderzoekshypothese daarentegen alleen maar gesproken over een verwacht verschil tussen twee groepen of een verwacht verband tussen twee variabelen, dan wordt er tweezijdig getoetst. Er wordt dan géén richting aangegeven. |
|
|
Dus als er een duidelijke richting in de onderzoekshypothese wordt geformuleerd,
wordt er |
eenzijdig getoetst.
Wordt er in de onderzoekshypothese daarentegen alleen maar gesproken over een verwacht verschil tussen twee groepen of een verwacht verband tussen twee variabelen, dan wordt er tweezijdig getoetst. Er wordt dan géén richting aangegeven. |
|
|
Wordt er in de onderzoekshypothese daarentegen alleen maar gesproken over een verwacht verschil tussen twee groepen of een verwacht verband tussen twee variabelen, dan wordt er hoe getoetst?
|
tweezijdig getoetst. Er wordt dan géén richting aangegeven.
|
|
|
De keuze voor eenzijdig of tweezijdig toetsen kan soms bepalend zijn voor de vraag of de resultaten significant zijn.
Veronderstel dat het IQ (dat wordt gemeten met een genormeerde test) in de populatie normaal is verdeeld met een gemiddelde van 100 en een standaardafwijking van 15, dus μ = 100 en σ= 15. Neem vervolgens aan dat iemand beweert dat hij mensen kan trainen om een hogere score te halen op de betreffende test. We nemen de proef op de som; bij wijze van experiment worden 25 aselect getrokken personen hiervoor getraind. De onderzoekshypothese luidt dat getrainde personen (A) hogere scores op de test halen dan de normpopulatie. Dus: H0: μA ≤ 100 en H1: μA > 100 |
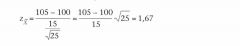
Het resultaat van de IQ-test in onze aselecte steekproef is dat X= 105. De standaardscore van dit gemiddelde is:
|
|
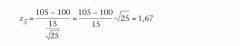
We toetsen dus rechtseenzijdig.
De rechter overschrijdingskans van X= 105 wordt nu: P(X ≥ 105) = P(zx ≥ 1,67) = 0,047. We hebben hiermee berekend dat de eenzijdige overschrijdingskans gelijk is aan p = 0,047, als μA in werkelijkheid gelijk is aan 100. Dit is kleiner dan het gebruikelijke significantieniveau van α = 0,05, en we kunnen dus concluderen dat getrainde personen hogere scores behalen dan de normpopulatie. Maar veronderstel nu dat we hadden besloten om tweezijdig toetsen... De overschrijdingskans wordt dan: |
tweemaal zo groot: ρ = 0,095.
Dit is groter dan 0,05, en we concluderen dus dat de nulhypothese niet mag worden verworpen. Nu moeten we concluderen: van de getrainde groep personen kan niet worden aangetoond dat ze gemiddeld hogere scores behalen dan de normpopulatie. Door een sluwe keuze voor eenzijdig dan wel tweezijdig toetsen zouden we hier kunnen bepalen wat het onderzoek oplevert: wel of geen effect. Daarom is op deze keuze een strenge methodologische regel van toepassing; we moeten van tevoren bepalen of we eenzijdig of tweezijdig gaan toetsen. Het is vals spel om achteraf, afhankelijk van het resultaat, vast te stellen of er tweezijdig dan wel eenzijdig wordt getoetst. |
|
|
Door een sluwe keuze voor eenzijdig dan wel tweezijdig toetsen zouden we hier kunnen bepalen wat het onderzoek oplevert: wel of geen effect.
Daarom is op deze keuze een strenge methodologische regel van toepassing; |
we moeten van tevoren bepalen of we eenzijdig of tweezijdig gaan toetsen. Het is vals spel om achteraf, afhankelijk van het resultaat, vast te stellen of er tweezijdig dan wel eenzijdig wordt getoetst.
|
|
|
Overigens dient men zich te blijven realiseren dat de α (significantie niveau) een
|
keuze is en niet een of andere vastliggende grens voor het onderscheid tussen wél significant of niet significant.
Men dient zich verder óók te blijven realiseren dat er een onderscheid bestaat tussen significantie en relevantie. Wanneer de steekproeven zeer groot zijn, zoals bijvoorbeeld bij opiniepeilingen, dan kan een klein verschil tussen twee steekgroepen al significant zijn zonder dat dit praktische betekenis heeft. Het verband tussen significantie en relevantie kan misschien nog het beste als volgt worden samengevat: significantie is een nodige maar geen voldoende voorwaarde voor relevantie. |
|
|
Men dient zich verder óók te blijven realiseren dat er een onderscheid bestaat tussen significantie en
|
relevantie.
Wanneer de steekproeven zeer groot zijn, zoals bijvoorbeeld bij opiniepeilingen, dan kan een klein verschil tussen twee steekgroepen al significant zijn zonder dat dit praktische betekenis heeft. Het verband tussen significantie en relevantie kan misschien nog het beste als volgt worden samengevat: significantie is een nodige maar geen voldoende voorwaarde voor relevantie. |
|
|
Wanneer de steekproeven zeer groot zijn, zoals bijvoorbeeld bij opiniepeilingen, dan kan een klein verschil tussen twee steekgroepen al significant zijn zonder dat dit praktische betekenis heeft.
Het verband tussen significantie en relevantie kan misschien nog het beste als volgt worden samengevat: |
significantie is een nodige maar geen voldoende voorwaarde voor relevantie.
|
|
|
5.8 Bepalen van een betrouwbaarheidsinterval
Bij het toetsen van een gemiddelde gaat het erom, een specifieke statistische hypothese te toetsen, bijvoorbeeld H0: μ ≤ 100 en H1: μ > 100. Bij het schatten van een populatiegemiddelde gaat het erom, dit zo nauwkeurig mogelijk op basis van het gevonden steekproefgemiddelde vast te stellen. We kennen hiervoor twee procedures: |
puntschattingen en intervalschattingen.
|
|
|
Puntschattingen
Bij puntschattingen wordt het populatiegemiddelde μ gelijk gesteld aan één in aanmerking komende waarde, bijvoorbeeld het steekproefgemiddelde X. Een nadeel van deze procedure is echter dat |
we er met onze schatting vrijwel altijd naast zitten, ook al zitten we - zeker met grote steekproeven - tamelijk dicht in de buurt.
Bovendien weten we niet hoe ver we er precies naast zitten. |
|
|
Intervalschattingen
Bij intervalschattingen schatten we een gebied (interval), waarvan we met een bepaalde zekerheid (bijvoorbeeld 95%) weten dat het populatiegemiddelde daarbinnen ligt. Het gaat er dus om |
grenzen aan te geven waartussen de te schatten populatieparameter μ ligt met een bepaalde mate van zekerheid.
Stel dat we zo'n interval willen schatten, terwijl we er voor 95% zeker van willen zijn dat het populatiegemiddelde μ binnen dit interval ligt. |
|
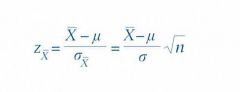
Omdat het gemiddelde van de steekproef normaal is verdeeld met een gemiddelde μ en de standaardafwijking σ/√n weten we met 95% zekerheid dat
|

ligt tussen -1,96 en + ,96, zie figuur 5.4.
De waarden +1,96 en -1,96 worden daarbij opgezocht in de tabel voor de standaardnormale verdeling. We weten dus met 95% zekerheid dat |
|
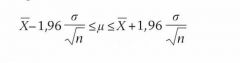
Na enige algebraïsche manipulaties kunnen we vorm 5.4 vervolgens omwerken tot:
|
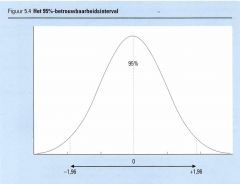
We weten nu met 95% zekerheid dat het populatiegemiddelde μ tussen deze grenzen ligt.
We noemen het gebied tussen de grenzen een 95%betrouwbaarheids interval. |
|
|
5.9 Relatie tussen een betrouwbaarheidsinterval en hypothesetoetsing
Er is, zoals ook al in de toelichting bij opgave 5.5 werd gesteld, een bepaalde relatie tussen hypothesetoetsen en het betrouwbaarheidsintervallen. We lichten deze relatie toe aan de hand van een aantal voorbeelden. Veronderstel dat we een steekproef trekken ter grootte van n = 121 met X = 101 en sx = 14. Neem α = 0,05. Neem voorts aan dat de nulhypothese luidt: H0: μ = 98 en de alternatieve hypothese is: H1: μ ≠ 98 De z-waarde van het steekproefgemiddelde is: |

We toetsen tweezijdig en de tweezijdige overschrijdingskans van
Zx = 2,36 is gelijk aan: Pd(zx = 2,36) = 2· PR(ZJ< = 2,36) = 2 x 0,0091 = 0,0182 Omdat: Pd = 0,0182 < α = 0,05 wordt de H0 verworpen. Maar veronderstel nu dat de nulhypothese zou luiden: |
|
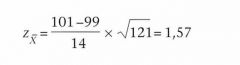
Maar veronderstel nu dat de nulhypothese zou luiden:
H0: μ = 99 en de alternatieve hypothese is: H1: μ. ≠ 99... De z-waarde van het steekproefgemiddelde is nu: |
De tweezijdige overschrijdingskans van Zx = 1,57 is gelijk aan: Pd Zx = 1,57) = 2·PR(Zx = 1,57) = 2 X 0,0582 = 0,1164
Omdat: Pd = 0,1165 > α = 0,05 wordt de H0 thans niet verworpen. |
|
|
De moraal van het verhaal is
|
dat er bij een bepaald steekproefgemiddelde en een gegeven α nulhypothesen zijn die wél en die niet worden verworpen.
|
|
|
Je vraagt je wellicht af wat voor zin het dan nog heeft om nulhypothesen te toetsen?
|
1 In de eerste plaats moet worden opgemerkt dat hetgeen hier verteld is slechts opgaat voor tweezijdige hypothesen. Over eenzijdige hypothesen
wordt geen uitspraak gedaan. 2 In de tweede plaats kan men bij steekproeven uit normaal verdeelde populaties inderdaad een 100(1 - a)% betrouwbaarheidsinterval berekenen. Maar dat is niet altijd mogelijk, zoals we bijvoorbeeld bij een aantal non-parametrische toetsen zien. In dat geval kan men dus alleen maar toetsen. 3 Een derde argument is van methodische aard. Bij een betrouwbaarheidsinterval heeft men het niet aangedurfd om een te verwachten antwoord op een onderzoeksvraag (de alternatieve hypothese dus) te formuleren. Men weet met andere woorden eigenlijk nog te weinig van de probleemstelling af, of heeft er nog niet nauwkeurig genoeg over nagedacht. Het onderzoek verloopt dan ook zonder enig risico. Of μ groot is of klein, het zal de onderzoeker niet schaden. Bij hypothesetoetsing ligt de zaak anders. Daar wordt men uitgedaagd (door het onderzoek dat men gaat doen) om na te gaan of men gelijk had of niet. Dit spel kan worden verloren, en het is uiteraard niet leuk als de werkelijkheid er anders uitziet dan men dacht, of wanneer de met pijn en moeite bedachte maatregel bij de evaluatie niet het succes opleverde dat men hoopte. Toch is dit uiteindelijk leerzamer. Men wordt gedwongen om nauwkeuriger over het veronderstelde verband, of de maatregel, na te denken. Het betrouwbaarheidsinterval nodigt daar veel minder toe uit. |
|
|
Voor 95% zeker?
In verslagen is de interpretatie van een 95%-betrouwbaarheidsinterval vaak dat we er 'dus' 95% zeker van zijn dat het populatiegemiddelde binnen dat interval ligt. Strikt genomen is die interpretatie |
onjuist.
Het 95%-betrouwbaarheidsinterval omvat alle waarden die we als nulhypothese bij α = 0,05 niet kunnen verwerpen. Ergens 95% zeker van zijn is een subjectieve inschatting. Filosofisch ingestelde statistici kunnen hier langdurig over debatteren. De mogelijke meerwaarde van een betrouwbaarheidsinterval boven de toetsing van een nulhypothese is dat we een meer nauwkeurige indicatie krijgen van het gebied waarin de populatieparameter ligt. |
|
|
5.10 Parametrische toetsen en non-parametrische toetsen
1 Parametrische toetsen Dit zijn toetsingsmethoden voor |
hypothesen over gemiddelden, standaardafwijkingen en correlatiecoëfficiënten waarbij de aannamen zijn
dat de variabelen in de populatie normaal zijn verdeeld, dat de populaties gelijke varianties hebben, en dergelijke. De wijze van toetsing is voor een groot deel op zulke aannamen over de kansverdeling in de populatie gebaseerd. Uit de behandeling van de normale verdeling (als kansverdeling voor een continue variabele) volgt dat de aanname van een normale verdeling inhoudt dat de gegevens op een intervalschaal of hoger moeten zijn gemeten; anders hebben steekproefgrootheden zoals het gemiddelde geen zinvolle inhoudelijke interpretatie. |
|
|
2 Non-parametrische toetsen
Een groot aantal variabelen heeft geen normale verdeling in de populatie. Denk bijvoorbeeld aan onderzoek waarvan de verzamelde gegevens uit rangordeningen bestaan, zoals de rangordening van de kinderen uit een klas naar populariteit. De resulterende ordinale variabele is zeker niet normaal verdeeld. Of neem het aantal doelpunten per voetbalwedstrijd, ook dat is bij lange na niet nonnaal verdeeld, Toch willen we ook bij zulke verdelingen hypothesen kunnen toetsen. De non-parametrische statistiek levert daarvoor het gereedschap. Non-parametrische toetsen kenmerken zich door |
het feit dat ze weinig tot geen aannamen met betrekking tot de vorm van de verdeling in de
populatie maken, in ieder geval niet die van normaliteit. Om deze reden worden het ook wel eens verdelingsvrije toetsen genoemd. Als geen normaliteit van de gegevens hoeft te worden verondersteld, hoeven de variabelen ook niet meer per se op intervalniveau te worden gemeten. De non-parametrische toetsen die wij behandelen hebben allemaal betrekking op variabelen die op een nominaal of op een ordinaal meetniveau mogen zijn gemeten. Doordat non-parametrische toetsen minder stringente eisen stellen aan de variabelen, zijn ze veel breder inzetbaar dan hun parametrische tegenhangers. Ze kunnen zelfs bij normaal verdeelde variabelen op intervalniveau worden aangewend. |
|
|
Non-parametrische toetsen
Maar alles heeft zijn prijs, dus ook de bredere inzetbaarheid van Non-parametrische toetsen. Als de gegevens in werkelijkheid bijvoorbeeld normaal zijn verdeeld, krijgt men met non-parametrische toetsen minder snel |
een significant resultaat dan met de eventueel in aanmerking komende parametrische toets.
De non-parametrische toets heeft dan minder onderscheidingsvermogen (power) en doet het daarom slechter. Non-parametrische toetsen zijn vooral goed bruikbaar wanneer de gegevens niet op intervalniveau (of nog hoger) zijn gemeten, of wanneer ze wel op intervalniveau zijn gemeten, maar de steekproef klein is en de populatie niet normaal is verdeeld. |
|
|
Non-parametrische toetsen zijn vooral goed bruikbaar wanneer
|
de gegevens niet op intervalniveau (of nog hoger) zijn gemeten, of wanneer ze wel op intervalniveau zijn gemeten, maar de steekproef klein is en de populatie niet normaal is verdeeld.
|

