Econometrics

Front 1

Econometrics

Back 1

The quantitative measurement and analysis of actual economic and business phenomena - bridge between abstract theory and real activity

Front 2

Three major uses of econometrics

Back 2

1) describing economic reality

2) testing hypotheses about economic theory

3) forecasting future economic activity

Front 3

Description

Back 3

One of the three uses of econometrics; lets you quantify economic activity by estimating numbers and putting them in equations that previously contained only abstract symbols

Front 4

Hypothesis testing

Back 4

One of the three uses of econometrics; the ability to evaluate alternative theories with quantitative evidence

Front 5

Forecasting

Back 5

One of the three uses of econometrics; the ability to predict what is likely to happen in the next quarter, year, or further into the future based on what has happened in the past

Front 6

Regression analysis

Back 6

a statistical technique that attempts to explain movement in the dependent variable as a function of movements in the independent variables, through the quantification of a single equation

Front 7

Can regression analysis confirm causality?

Back 7

No

Front 8

constant / intercept coefficient

Back 8

The value of y when x = 0

Front 9

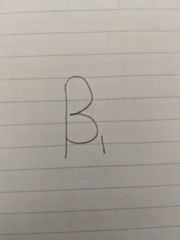
Slope coefficient

Back 9

The amount that y will change when x increases by one unit

Front 10

An equation is linear if...

Back 10

Plotting the function in terms of x and y generates a straight line

Front 11

If linear regression techniques are going to be applied to an equation, that equation must be...

Back 11

Linear

Front 12

Stochastic error term

Back 12

A term that is added to a regression equation to introduce all of the variation in y that cannot be explained by the included x's

Front 13

The four sources of variation in y other than the variation in x

Back 13

1) ommitted minor influences

2) measurement error in y

3) The underlying equation might have a different functional form than the one chosen for the regression (might not be linear)

4) purely random variation

Front 14

Multivariate linear regression model

Back 14

Front 15

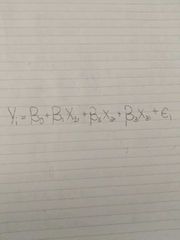
Single equation linear regression model

Back 15

Front 16

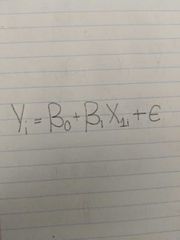
Multivariate regression coefficient

Back 16

B1, B2, B3

serves to isolate the impact on y of a change in one variable from the impact on y of changes in other variables - tells you the impact of one independent variable on the dependent variable, holding constant the influence of the other variables in the equation

Front 17

Dummy variable

Back 17

A variable that can only take on two values (1 or 0), used to quantify a concept that is inherently qualitative, such as gender

Front 18

Estimated regression equation

Back 18

An equation where the coefficients (the B values) are empirical best guesses of the true regression coefficients, and thus actual numbers

Front 19

Cross-sectional data set

Back 19

A data set where all of the observations are from the same point in time and represent different individual economic entities (countries, houses) from that same point in time

Front 20

Specification error

Back 20

An error in selecting your independent variable and how it should be measured, the mathematical form of the variables, or the properties of the stochastic error term

Front 21

Outlier

Back 21

An observation that flies outside the range of the rest of the observations - a good way to find data entry errors

Front 22

Ordinary Least Squares (OLS)

Back 22

A regression estimation technique that calculates the coefficients so as to minimize the minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the given dataset and those predicted by the linear equation.

Front 23

Why use ordinary least squares?

Back 23

1) they're relatively easy to use

2) The goal of minimizing the sum of all residuals is appropriate from a theoretical point of view (since the residual can be negative as well as positive, the sum of residuals could be low even if the equation is inaccurate. Squaring the residual fixes this)

3) OLS estimates have a number of useful characteristics (The sum of the residuals is always exactly zero, and OLS can be shown to be the "best" estimator possible under a set of specific assumptions)

Front 24

Residual

Back 24

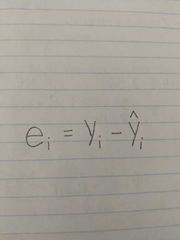
The difference between the estimated value of the dependent variable and the actual value of the dependent variable

Front 25

Total Sum of Squares

Back 25

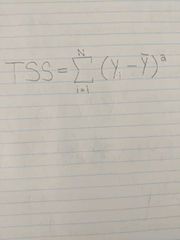
A measure of the amount of variation that can be explained by the regression

Front 26

Components of the total Sum of Squares for Ordinary Least Squares

Back 26

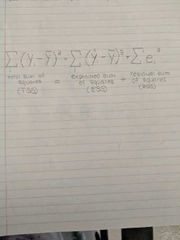
Also known as the decomposition of variance

Front 27

Explained sum of squares

Back 27

Tells you how much of the variation in the dependent variable your model explained

Front 28

Residual sum of squares

Back 28

The sum of the squared differences between the actual y and the predicted y; tells you how much of the dependent variables variation your model did not explain

Front 29

Simple correlation coefficient (r)

Back 29

A measure of the strength and direction of the linear relationship between two variables

Front 30

If two variables are perfectly positively correlated then r equals =

Back 30

+1

Front 31

If two variables are perfectly negatively correlated, then r equals

Back 31

-1

Front 32

If two variables are totally uncorrelated, then r equals

Back 32

0

Front 33

Back 33

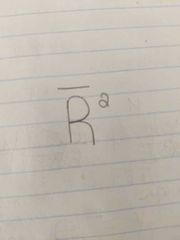
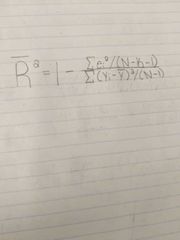
R squared adjusted for degrees of freedom

Front 34

Degrees of freedom

Back 34

The excess of the number of observations over the number of coefficients to be estimated

Front 35

Are more degrees of freedom better?

Back 35

Yes, because when the number of degrees of freedom is large, every positive error is likely to be balanced by a negative error

Front 36

Y hat (written ŷ )

Back 36

the predicted value of y (the dependent variable) in a regression equation. It can also be considered to be the average value of the response variable.

Front 37

X bar

Back 37

The mean of the x variable

Front 38

Y bar

Back 38

The mean of the y variable