![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
112 Cards in this Set
- Front
- Back
|
Parametrische toetsen:
|
-Z-toets voor het gemiddelde
-de t-toets voor het gemiddelde -Z-toets voor het verschil tussen twee gemiddelden -Toets voor gepaarde waarneming: Twee onafhankelijke steekproeven -Toets voor twee varianties: de F-toets -Toets voor de correlatie |
|
|
6-1 Z-toets voor het gemiddelde Toetsingssituatie
Heeft het gemiddelde van de populatie waaruit de steekproef afkomstig is een bepaalde waarde of niet? Uitgangspunt is |
dat we een populatie hebben met een normaal verdeelde variabele X waaruit een aselecte
steekproef wordt getrokken ter grootte van n. Het steekproefgemiddelde is X en de standaarddeviatie is Sx |
|
|
H6 Toetsende statistiek: Parametrische toetsen
Toetsingssituatie Heeft het gemiddelde van de populatie waaruit de steekproef afkomstig is een bepaalde waarde of niet? Uitgangspunt is dat we een populatie hebben met een normaal verdeelde variabele X waaruit een aselecte steekproef wordt getrokken ter grootte van n. Het steekproefgemiddelde is X en de standaarddeviatie is Sx. Voorwaarden De z-toets voor het gemiddelde mag worden toegepast indien: |
1
σ (de standaardafwijking van de populatie) bekend is en de populatie normaal is verdeeld; 2 σ onbekend is en/ of de populatie niet normaal verdeeld, én n ≥ 100. Uit de centrale limietstelling volgt dat het gemiddelde X dan bij benadering normaal verdeeld is en voor de standaardafwijking van de populatie σ mogen we dan ten koste van een te verwaarlozen fout de standaardafwijking van de steekproef Sx invullen als schatter. |
|
|
De z-toets voor het gemiddelde mag niet worden toegepast indien:
|
1
de populatie niet normaal verdeeld is én n klein is (vuistregel: n < 100). In dat geval nemen we voor een steekproefgrootten tussen 30 en 100 de dadelijk te behandelen t-verdeling. Voor n kleiner dan 30 nemen we de non-parametrische 'signed rank test for the mean', die we overigens niet behandelen omdat deze relatief weinig wordt gebruikt. 2 de populatie wel normaal verdeeld is, maar σ onbekend is en n < 100. We nemen dan de zo dadelijk te bespreken t-toets uit paragraaf 6.2. |
|
|
Hypothesen
Als μ0 een bepaalde waarde is voor het populatiegemiddelde μ, dan luiden de nulhypothesen en de alternatieve hypothesen als volgt: L R T |
Linkseenzijdig toetsen H0 :μ ≥ μo en H1 μ < μo
Rechtseenzijdig toetsen H0 :μ ≤ μo en H1 μ > μo Tweezijdig toetsen H0 :μ = μo en H1 μ ≠ μo |
|
|
Toetsingsgrootheid
Om de z-toets te kunnen gebruiken, moeten we eerst |
het steekproefgemiddelde berekenen. Vervolgens moeten we, om de overschrijdingskans van het gemiddelde te kunnen berekenen, het steekproefgemiddelde omzetten in een z-score.
Deze z-score is de toetsingsgrootheid, omdat het de statistische grootheid is waarmee we nagaan of de Ho kan worden verworpen. |
|
|
Deze z-score is de toetsingsgrootheid, omdat
|
het de statistische grootheid is waarmee we nagaan of de Ho kan worden verworpen.
|
|
|
het de statistische grootheid is waarmee we nagaan of de Ho kan worden verworpen.
z-score van het steekproefgemiddelde onder H0 |

X = verkregen steekproefgemiddelde
μo = veronderstelde waarde voor het populatiegemiddelde μ n = steekproefgrootte σ = standaarddeviatie van de populatie Alleen wanneer n > 100 mag voor σ de standaardafwijking van de steekproef Sx worden ingevuld . Onder Ho volgt Zx. een standaardnormale verdeling met een gemiddelde van 0 en een standaardafwijking van 1. |
|
|
Beslissingsregel
De beslissingsregel over het al of niet verwerpen van de H0 kan op twee manieren worden geformuleerd: |
Met behulp van overschrijdingskansen of met behulp van kritieke waarden en kritieke zones.
Met behulp van overschrijdingskansen bepalen we eerst de overschrijdingskans van de toetsingsgrootheid onder de aanname dat H0 juist is. |
|
|
De nulhypothese (H0) wordt verworpen indien:
|
bij linkseenzijdige toetsing: PL(zx.) ≤ α,
bij rechtseenzijdige toetsing: PR(zx. ) ≤ α, bij tweezijdige toetsing: Pd(zx. ) = 2 · PL(zx. ) ≤ α als X < μ = 2 · PR(zx.) ≤ α als X > μ waarin: PL en PR = resp. linker en rechter overschrijdingskans Pd = tweezijdige overschrijdingskans Zx = z-score van het steekproefgemiddelde H0 wordt dus verworpen wanneer de een- of tweezijdige overschrijdingskans van de z-score van het gemiddelde kleiner is dan of gelijk is aan α. |
|
|
Met behulp van kritieke waarden bepalen we eerst welke z-waarde(n) bij het significantieniveau α hoort of horen . Voor α = 0,05 en bij linkseenzijdige toetsing is de kritieke z-waarde gelijk aan -1,64.
De Ho wordt dan verworpen indien |
de z-score van het gemiddelde kleiner is dan of gelijk is aan - 1,64, dus: zx. ≤ 1,64.
Voor α= 0,05 en bij rechtseenzijdige toetsing is de kritieke z-waarde gelijk aan +1,64 en wordt de Ho verworpen indien Zx. ≥ +1,64. Voor α = 0,05 en bij tweezijdige toetsing zijn de kritieke z-waarden - 1,96 en +1 ,96 en de Ho wordt dan verworpen indien Zx. < -1,96 of zx. > +1 ,96. De H0 wordt dus verworpen wanneer de z-score van het gemiddelde in de kritieke zone(s) terechtkomt. |
|
|
Betrouwbaargeids interval.
Als we met een bepaald percentage zekerhgeid willen weten binnen welke grenzen het werkelijke populatie gemiddelde ligt, dan bepalen we een betrouwbaarheidsinterval. Bij een betrouwbaarheidsdrempel α wordt de formule voor 100(1-α)% betrouwbaarheidsinterval gelijk aan: |
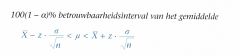
100(1- ex)% betrouwbaarheidsinterval van het gemiddelde
|
|
|
6.8 Slotwoord parametrische toetsen
We hebben ons in het voorgaande tot de meest gebruikte parametrische toetsen voor één en twee steekproeven beperkt. Dat zijn uiteraard niet alle toetsen die er zijn. We noemen nog enkele voorbeeld en van andere hypothesen die we kunnen toetsen: |
6.8 Slotwoord parametrische toetsen
1. Correlatietoets voor waarden die afwijken van 0 2. Toets voor het verschil tussen twee of meer correlaties in onafhankelijke steekproeven 3. Toets voor het verschil tussen correlaties bij afhankelijke steekproeven 4 CHi 2-toets voor één variantie |
|
|
6.8 Slotwoord parametrische toetsen
1. Correlatietoets voor waarden die afwijken van 0 2. Toets voor het verschil tussen twee of meer correlaties in onafhankelijke steekproeven 3. Toets voor het verschil tussen correlaties bij afhankelijke steekproeven 4 CHi 2-toets voor één variantie |
1. Correlatietoets voor waarden die afwijken van 0
Deze toets gebruiken we wan neer we ons afvragen of de popul atiecorrelatie wel of niet een bepaalde waarde heeft. De meest voorkomende nulhypothese is dan: H0 : p = p0 (p0 is een bepaalde van 0 afwijkende waarde). 2. Toets voor het verschil tussen twee of meer correlaties in onafhankelijke steekproeven Veronderstel dat we in twee of meer onafhankelijke steekproeven de correlatie hebben berekend tussen X en Y en na willen gaan of de over eenk omstige correlaties in de populaties waaruit de steekproeven ko m en verschillen . De nulhypothese is dan: H0: p 1= p2= ... = p n 3. Toets voor het verschil tussen correlaties bij afhankelijke steekproeven Hier gaat het om het verschil tussen correlaties binnen één en dezelfde steekproef, bijvoorbeeld het verschil in correlatie wanneer de variabe l en X 1 en X2 m et een derde variabele X 3 worden gecorreleerd. Dit geval doet zich met name voor als we twee validiteitcoëfficiënten willen vergelijken : twee tests correleren elk met een zelfde criterium X3. Om na te gaan of er verschillen zijn , toetsen we meestal de nulhypothese : H0: p 1 3 = P z3 4 CHi 2-toets voor één variantie Deze toets gebruiken we als we willen nagaan of de vari antie in een normaal verdeeld e populatie een bepaalde waarde heeft, bijvoorbeeld als we willen nagaan of de steekproef afkomstig is uit een populatie waarin het IQ een standaardafwijking van 15 heeft . H0 : σ2 = σ0 in het kwadraat (σ o is een bepaalde waarde) . |
|
|
Hoe bepalen we w elke toets we bij een bepaalde vraagstelling moet gebruiken? Welke van de genoemde parametrische, of de hierna te behandelen non -parametrische toetsen komt in aanmerking om de onderzoeksvraag te beantwoorden ?
|
Om deze vraag te kunnen beantwoorden moeten we allereerst nauwkeurig om schrijven wat de onderzoeksvraag is waarover we uitsluitsel willen, en in welke toetsingssituatie we ons bevinden.
|
|
|
Je moet weten:
Het... |
Het aantal populaties
Het meetniveau Is de populatie normaal verdeeld ? Is of zijn het afhankelijke of onafhankelijke steekproeven |
|
|
Aantal populaties
|
Hoeveel populaties zijn er in het geding? Gaat het om de waarde van een parameter binnen één populatie (bij voorbeeld het gemiddelde µ of de correlatie tussen twee variabelen p), of gaat het om het verschil tussen twee populaties (bijvoorbeeld of ze een verschillend populatiegemiddelde hebben , of dat hun varianties verschillen)?
Dit bepaalt namelijk of we met een één -steekproefprobleem of een twee -steekproevenprobleem te maken hebben. |
|
|
Meetniveau
|
Is (of zijn ) de variabele(n) gemeten op intervalniveau of hoger ? Zijn ze gemeten op ordinaal niveau of lager, gebruik dan in ieder geval een non-parametrische techniek.
|
|
|
Populatie normaal verdeeld ?
|
Zi jn de populaties normaal verdeeld met bekende standaard afwijkingen , of niet? Dit bepaalt of we een z-toets of een t-toets mogen gebruiken .
Zijn de populaties niet normaal verdeeld , maar zijn de steekproeven voldoende groot om te mogen veronderstellen dat de steekproeven verdeling van het gemiddelde bij ben ader ing normaal is verd eeld? In dat geval mogen we de t-toets gebruik en. Zijn de steekproeven echter te klein, gebruik d a n een va n de n on-pa ram etrische toetsen. |
|
|
Afhankelijke of onafhankelijke steekproeven
|
Zijn de steekproeven die we in situaties van twee of meer populaties trekken afhankelijk of onafhankelijk ? Zijn ze onafhankelijk getrokken, gebruik dan toetsen voor onafhankelijke steekproeven . Zijn ze afhankelijk getrokken, gebruik dan toetsen voor afhankelijke steekproeven .
|
|
|
6 .1 Z-toets voor het gemiddelde
Toetsingssituatie Heeft het gemiddelde van de populatie waaruit de steekproef afkomstig is een bepaalde waarde of niet? Uitgangspunt is |
dat we een populatie hebben met een normaal verdeelde variabele X waaruit een aselecte steekproef wordt getrokken ter grootte van n.
Het steekproefgemiddelde is X (gemiddelde) en de standaarddeviatie is sx· |
|
|
Voorwaarden
De z-toets voor het gemiddelde mag worden toegepast indien: |
1 σ (de standaardafwijking van de populatie) bekend is en de populatie normaal is verdeeld;
2 σ onbekend is; en/of de populatie niet normaal verdeeld, én n ~ 100. Uit de centrale limietstelling volgt dat het gemiddelde X dan bij benadering normaal verdeeld is en voor de standaardafwijking van de populatie σ mogen we dan ten koste van een te verwaarlozen fout de standaardafwijking van de steekproef Sx invullen als schatter. |
|
|
De z-toets voor het gemiddelde mag niet worden toegepast indien:
|
1 de populatie niet normaal verdeeld is én n klein is (vuistregel: n < 100). In dat geval nemen we voor een steekproefgrootte n tussen 30 en 100 de t-verdeling.
Voor n kleiner dan 30 nemen we de non-parametrische 'signed rank test for the mean', die we overigens niet behandelen omdat deze relatief weinig wordt gebruikt. 2 de populatie wel normaal verdeeld is, maar σ onbekend is en n < 100. We nemen dan de t-toets |
|
|
Slotwoord z-toets voor het gemiddelde
Een kleine steekproef mag. Bijv. n = 9 is klein. Maar als de steekproef inderdaad aselect is getrokken, en de populatie inderdaad normaal verdeeld is met - in dit geval - een gemiddelde van 100 en een standaardafwijking van 10, dan is een eventueel commentaar op de grootte van de steekproef |
niet terecht.
De hypothese is volkomen volgens de regels getoetst en daar is niets op aan te merken. De H0 wordt echt verworpen. |
|
|
Men kan het ook zo zien: de verschillen tussen kinderen die laat naar bed gaan en het populatiegemiddelde moeten wel erg groot zijn, wil
men met zo'n kleine steekproef al |
een statistisch significant verschil kunnen aantonen.
Dat men het verschil al met een kleine aselecte steekproef vindt, bevestigt des te meer dat er volgens de alternatieve hypothese een echt verschil aanwezig is. |
|
|
Het berekenen van een betrouwbaarheidsinterval heeft als groot voordeel
|
dat men in één oogopslag ziet welke hypothesen wél en welke niet kunnen worden verworpen.
|
|
|
Het vergt echter nieuw onderzoek, althans nieuwe gegevens, om dat ook daadwerkelijk te doen.
Nulhypothesen opstellen aan de hand van verkregen gegevens en die op dezelfde gegevens toetsen, is statistisch gezien een |
doodzonde.
Hypothesen stelt men op voordat men de gegevens verzamelt, zodat men ook echt het risico loopt dat men ongelijk heeft. Dat risico is verdwenen wanneer men op basis van gegevens al weet wat er uit gaat komen. Bij elke hoeveelheid gegevens is immers wel een nulhypothese te vinden die men op basis van die gegevens zou verwerpen. Pas wanneer men deze op nieuwe gegevens toetst , loopt men - zoals het hoort - toch weer het risico dat de H0 niet wordt verworpen. |
|
|
6 .2 De t-toets voor het gemiddelde
Toetsingssituatie Naast de z-toets is er nog een tweede parametrische toets om te toetsen of het populatiegemiddelde een bepaalde waarde heeft: |
de t-toets.
|
|
|
Ook de t-toets is een toets voor één steekproef uit één populatie.
Uitgangspunt: |
is ook hier dat we een normaal verdeelde populatie hebben waaruit een aselecte steekproef wordt getrokken ter grootte van n.
Het steekproefgemiddelde is X en de standaardafwijking van de steekproef is sx. |
|
|
Voorwaarden
De t-toets voor het gemiddelde mag worden gebruikt indien: |
we een kleine steekproef trekken (n < 100) uit een populatie die normaal verdeeld is met een onbekende standaarddeviatie u;
de steekproef groter is dan 30 en de populatie niet normaal verdeeld is. De t-toets voor het gemiddelde mag niet worden gebruikt indien: de steekproefgrootte kleiner is dan 30 en de populatie niet normaal verdeeld is. In dat geval nemen we de non-parametrische 'signed rank test' |
|
|
De t-toets voor het gemiddelde mag niet worden gebruikt indien:
|
de steekproefgrootte kleiner is dan 30 en de populatie niet normaal verdeeld is. In dat geval nemen we de non-parametrische 'signed rank test'
|
|
|
Toetsingsgrootheid
Om de toets te kunnen uitvoeren, zetten we het steekproefgemiddelde om in een t-score. Deze t-score is de toetsingsgrootheid waarmee we de H0 toetsen. t-score van het steekproefgemiddelde: |

|
|
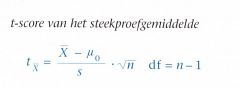
Deze formule lijkt sterk op die van de z-score. Het enige verschil is dat de standaarddeviatie van de populatie a nu vervangen wordt door
|
de standaarddeviatie van de steekproef s.
|
|
|
Wanneer nu s een goede benadering zou zijn van a, zouden we kunnen doorgaan met Zx als onze toetsingsgrootheid en de normale verdeling als model voor de steekproevenverdeling.
Aan het eind van de negentiende eeuw kwam de statisticus W. Gosset erachter dat de schatting van a door s voor kleinere steekproeven niet goed is. Met kleine steekproeven (n < 100) is s in de helft van het aantal gevallen een onderschatting van a en dit heeft als direct gevolg dat de toetsingsgrootheid |
een grotere standaarddeviatie heeft dan de normale verdeling.
Gosset beschreef een verdeling, of beter gezegd, een familie van kansverdelingen die het mogelijk maakte om hypothesen te toetsen wanneer de steekproeven uit een normaal verdeelde populatie getrokken zijn met een onbekende standaarddeviatie. Deze verdeling heet de t-verdeling, of ook wel de student-t-verdeling. Gosset publiceerde een en ander namelijk onder de schuilnaam Student. |
|
|
Als de nulhypothese juist is en de populatie is normaal verdeeld, dan volgt de toetsingsgrootheid tx een t-verdeling.
Deze verdeling lijkt op een normale verdeling, maar heeft een wat plattere vorm en dikkere staarten. De t-verdeling is eveneens symmetrisch en het gemiddelde is nul. Bi j kleine steekproeven uit een normale verdeling met een onbekende a mogen we dus zeggen dat de t-scores van het gemiddelde t-verdeeld zijn. Hetzelfde mogen we ten koste van een kleine fout zeggen als de steekproeven niet uit een normale verdeling komen, maar ... |
groter dan 30 zijn.
|
|
|
Een t-verdeling is een (continue) kansverdeling van de variabele t en dus kunnen we (net zoals in bij de standaardnormale verdeling) voor elke t-waarde de overschrijdingskans (of kansen op t-waarden binnen
bepaalde gebieden) berekenen. Helaas zijn er meerdere t-verdelingen mogelijk, die niet - zoals bij normale verdelingen - tot één standaard- verdeling zijn te herleiden. Elke t-verdeling wordt daarbij volledig bepaald door: |
het zogenaamde aantal vrijheidsgraden (df) bepaald.
Dus zijn er zo veel t-verdelingen als er vrijheidsgraden zijn. |
|
|
Maar wat is een vrijheidsgraad?
Veronderstel dat we van vijf getallen het gemiddelde weten, zeg 10. Hoeveel van die vijf getallen mag ik dan vrij kiezen, of anders gezegd, op hoeveel manieren kan mijn keuzevrijheid zich manifesteren: hoeveel graden van vrijheid (degrees of freedom) heb ik? |
Het antwoord is 4,
want ik mag vier getallen willekeurig - dus volledig onafhankelijk van elkaar - kiezen, bijvoorbeeld 5, 11, 3 en 8. Het vijfde getal ligt dan echter vast. Dat moet zo worden gekozen dat het gemiddelde 10 wordt. In ons geval moet het vijfde getal dus 23 zijn . In dit geval hebben we dus 5 - 1 vrijheidsgraden: df = 5 - 1 = 4. We zijn één van de vijf vrijheidsgraden verloren, omdat het gemiddelde reeds van tevoren vastlag. |
|
|
Als we met afwijkingsscores werken, zoals bij de
schatting van de populatiestandaardafwijking door de steekproefstandaardafwijking, dan is deze niet op 5 (of meer algemeen n) vrijheidsgraden, maar op df = 5 - 1 = 4 (of meer algemeen df = n - 1) gebaseerd. Bij de t-verdeling gebruiken we de standaardafwijking uit de steekproef als |
schatter van de populatiestandaardafwijking en dus werken we met afwijkingsscores.
Dit kost ons 1 vrijheidsgraad, zoals we zo juist hebben gezien. Als de steekproefgrootte n is, is de t-verdeling voor het gemiddelde daarom op df = n - 1 gebaseerd. |
|
|
Beslissingsregel
Ook bij de t-toets kan de beslissingsregel over het al of niet verwerpen op twee manieren worden geformuleerd: |
met behulp van overschrijdingskansen
en met behulp van kritieke waarden. |
|
|
Er zijn net zoveel t-verdelingen als er vrijheidsgraden zijn en dus moeten we, om alle kansen te kunnen berekenen, over net zo veel tabellen
beschikken als er vrijheidsgraden zijn. Het opzoeken van alle mogelijke overschrijdingskansen met behulp van tabellen kan dus niet. Het berekenen van alle mogelijke overschrijdingskansen in de t-verdeling kan alleen |
wanneer men over een programma beschikt, bijvoorbeeld probs.exe.
|
|
|
Kritieke waarden
Met behulp van kritieke waarden bepalen we eerst welke t-waarde(n) hoort of horen bij een bepaald aantal vrijheidsgraden en bij het significantieniveau σ. Veronderstel de steekproefgrootte bedraagt 19 en het significantieniveau is 0,05. |
Voor σ = 0,05 en df = 19 - 1 = 18 en bij linkseenzijdige toetsing kijken we in bijlage 3 in de regel df = 18 en in de kolom onder σ = 0,05 (eenzijdige toetsing); daar vinden we het getal: 1,734.
|
|
|
Als het aantal vrijheidsgraden groter wordt, gaat de t-verdeling steeds meer waar op lijken?
|
op een normale verdeling lijken. Voor df > 100 zijn de verschillen zo klein, dat ook de tabel voor de standaardnormale verdeling mag worden gebruikt.
|
|
|
Betrouwbaarheidsinterval
Behalve het toetsen van hypothesen kunnen we ook betrouwbaarheidsintervallen berekenen. Wanneer we met een bepaald percentage zekerheid willen weten binnen welke grenzen het populatiegemiddelde ligt, dan bepalen we het |
betrouwbaarheidsinterval.
|
|
|
De algemene formule voor het 100(1 - a)%-betrouwbaarheidsinterval is:
100(1 - σ)%-betrouwbaarheidsinterval van het gemiddelde waarin: |

100(1 - σ)%-betrouwbaarheidsinterval van het gemiddelde waarin:
|
|
|
Deze uitdrukking geeft aan dat we met (1 - σ)% zekerheid weten dat
|
het populatiegemiddelde binnen de genoemde grenzen ligt.
Of dat alle nulhypothesen binnen deze grenzen bij tweezijdige toetsing niet zullen worden verworpen. |
|
|
6.3 Z-toets voor het verschil tussen twee gemiddelden
Toetsingssituatie In veel onderzoekingen zijn we vooral in de verschillen tussen twee populaties geïnteresseerd. We willen bijvoorbeeld weten of jongens meer aanleg voor wiskunde hebben dan meisjes, of kinderen die volgens een bepaalde methode les hebben gehad betere prestaties leveren op eenzelfde test dan andere kinderen, of kinderen uit hogere milieus assertiever zijn dan kinderen uit lagere milieus, of het percentage leerlingen van een school dat in één keer voor het eindexamen vwo slaagt in de Randstad gemiddeld hoger ligt dan in de rest van Nederland, et cetera. Daarvoor gebruiken we de: |
Z-toets voor het verschil tussen twee gemiddelden
|
|
|
De z-toets voor het verschil tussen twee gemiddelden gaat ervan uit dat
|
we twee normaal verdeelde populaties hebben.
Het gemiddelde en de standaardafwijking van populatie I zijn μ1 en σ1 en die van populatie II zijn μ1 en σ2. Met de toets willen we aantonen dat de twee populatiegemiddelden van elkaar verschillen. |
|
|
Met de z-toets voor het verschil tussen twee gemiddelden willen we wat aantonen?
|
Met de toets willen we aantonen dat de twee populatiegemiddelden van elkaar verschillen.
|
|
|
We trekken uit elke populatie aselect een steekproef, zodat we over twee onafhankelijke steekproeven beschikken .
Van elk van deze steekproeven berekenen we zoals gebruikelijk |
het gemiddelde en de standaarddeviatie
|
|
|
Voorwaarden
De z-toets wordt toegepast indien: |
A.
σ1 en σ2 bekend zijn en de populaties normaal zijn verdeeld; B. σ1 en σ2 onbekend zijn en/of de populaties niet normaal zijn verdeeld, en de aantallen n1 en n2 (als vuistregel) beide groter of gelijk zijn aan 100; we blijven daarmee aan de veilige kant. We nemen dan de standaardafwijkingen van de steekproeven s1 en s2 als schatters van σ1 en σ2 . |
|
|
De z-toets wordt niet toegepast indien:
|
-σ1 en σ2 onbekend zijn en
-de beide steekproeven kleiner zijn dan 100. Dan wordt de t-toets gebruikt. |
|
|
Hypothesen
We beweren in feite dat het gemiddelde in de ene populatie μ1 verschilt van dat in de andere populatie μ2 . De alternatieve hypothese heeft dus betrekking op het verschil tussen twee populatiegemiddelden: μ1 - μ2. Een alternatieve hypothese is bijvoorbeeld dat het gemiddelde in de eerste populatie groter is dan in de tweede: μ1 -μ2. De nulhypothese zegt dan dat |
er geen verschil is of zelfs een omgekeerd verschil, dus dat μ1 ≤ μ2 .
|
|
|
Toetsingsgrootheid
De verschillen tussen de gemiddelden van steekproeven die elk uit één populatie komen zullen van steekproef tot steekproef een verschil laten zien. Evenals de afzonderlijk steekproefgemiddelden hebben de verschillen tussen de gemiddelden daarom eveneens een steekproeven verdeling. Deze verdeling heet |
de steekproevenverdeling van het verschil tussen twee gemiddelden, of de steekproevenverdeling van X1 - X2.
Omdat de steekproeven afkomstig zijn uit normale verdelingen met bekende σ 's, kunnen we aantonen dat ook de steekproevenverdeling van de gemiddelden X1 - X2 normaal is. |
|
|
Steekproef verdeling van de gemiddelden X1 en X2
|

Als we het verschil tussen de twee steekproefgemiddelden hebben berekend, kunnen we dit verschil omzetten in een z-score.
Deze z-score is de toetsingsgrootheid waarmee hypothesen over verschillen in gemiddelden tussen twee normaal verdeelde populaties kunnen worden getoetst. |
|
|
Deze z-score is de toetsingsgrootheid waarmee hypothesen over verschillen in gemiddelden tussen twee normaal verdeelde populaties kunnen worden getoetst.
|

z-score van het verschil tussen twee gemiddelden
|
|

z-score van het verschil tussen twee gemiddelden
|

Het is inderdaad een z-score,
want we nemen het gevonden verschil, verminderen dit met het echte verschil tussen de populaties en delen dit door de standaardafwijking van alle mogelijke verschillen tussen de steekproefgemiddelden van steekproeven ter grootte van n1 en n2. |
|
|
Als we de nulhypothese toetsen dat er geen verschil is, zodat μ1 - μ2 = 0, dan vullen we op die plaats natuurlijk 0 in in de formule van z.
Er komt dan in de teller van de formule voor z alleen het verschil tussen de twee steekproefgemiddelden te staan. Een enkele keer komt het voor in onderzoek dat men aan verschillen tussen populatiegemiddelden pas betekenis hecht, wanneer die verschillen groter zijn dan een bepaalde waarde, zeg a. Dit is bijvoorbeeld het geval wanneer we moeten onderzoeken of een dure overheidsmaatregel moet worden ingevoerd en de overheid alleen tot invoering wil overgaan als de maatregel een voldoende groot effect sorteert (groter dan a). In dat geval luidt de nulhypothese |
dat μ1 - μ2 ≤ + a en de alternatieve hypothese bijvoorbeeld
dat μ1 - μ > + a . In de formule van z moeten we nu op de plaats waar μ1 - p2 staat a invullen. Voor de rest verloopt de toets precies hetzelfde als hiervóór is beschreven. |
|
|
Beslissingsregel
Ook bij de z-toets voor het verschil tussen twee gemiddelden kan de beslissingsregel over het al of niet verwerpen van de H0 op twee manieren worden geformuleerd: |
met behulp van overschrijdingskansen of met
behulp van kritieke waarden en kritieke zones. Met behulp van overschrijdingskansen bepalen we eerst de overschrijdingskans van de toetsingsgrootheid onder de aanname dat H0 juist is. |
|
|
Met behulp van kritieke waarden bepalen we eerst welke z-waarde(n) hoort of horen bij het significantieniveau α.
Voor α = 0,05 en bij linkseenzijdige toetsing is de kritieke z-waarde gelijk aan -1,64. De H0 wordt dan verworpen indien de z-score van het verschil tussen de gemiddelden van de twee steekproeven kleiner dan of gelijk aan -1,64 is. De H0 wordt dus verworpen wanneer |
de z-score van het verschil tussen de twee gemiddelden in de kritieke zone(s) terechtkomt.
|
|
|
Betrouwbaarheidsinterval
Als we met een bepaald percentage zekerheid willen weten binnen welke grenzen het verschil tussen twee populatiegemiddelden ligt, dan berekenen we een |

betrouwbaarheidsinterval.
Uitgaande van normale verdelingen, of grote steekproeven, wordt het 100(1 -α)%-betrouwbaarheidsinterval: 100(1 - α)%-betrouwbaarheidsinterval van het verschil tussen twee gemiddelden |
|
|
6.4 De t-toets voor het verschil tussen twee gemiddelden
Toetsingssituatie De t-toets voor het verschil tussen twee gemiddelden wordt in soortgelijke situaties gebruikt als |
de z-toets voor het verschil tussen twee gemiddelden.
Ook nu zijn we vooral in de verschillen tussen twee populaties geïnteresseerd. We willen bijvoorbeeld weten of jongens meer aanleg voor wiskunde hebben dan meisjes, of een instructiefilm meer effect heeft dan klassikale uitleg, enzovoort. |
|
|
Bij de t-toets voor het verschil tussen twee gemiddelden gaan we uit van
|
-twee normaal verdeelde populaties waarvan we de standaardafwijkingen niet kennen.
-Uit elke populatie wordt een aselecte steekproef getrokken en we krijgen zo dus twee onafhankelijke steekproeven. -Van elke steekproef bepalen we het gemiddelde en de standaardafwijking. -Nagegaan wordt of de gemiddelden van beide populaties verschillen. |
|
|
Voorwaarden
De t-toets voor het verschil tussen twee gemiddelden mag worden gebruikt indien: |
1 de twee populaties normaal zijn verdeeld met onbekende σ1 en σ2, en n1 of n2 kleiner zijn dan 100.
2 de populaties niet normaal zijn verdeeld, maar beide steekproeven tussen de dertig en de honderd onderzoekseenheden bevatten. Wanneer de populaties niet normaal zijn verdeeld, maar n1 en n2 groter zijn dan 100, gebruiken we de z-toets voor het verschil tussen twee gemiddelden. |
|
|
Wanneer de populaties niet normaal zijn verdeeld, maar n1 en n2 groter zijn dan 100, gebruiken we
|
de z-toets voor het verschil tussen twee gemiddelden.
|
|
|
Toetsingsgrootheid
Er zijn twee varianten van de t-toets voor het verschil tussen twee gemiddelden die samenhangen met de vraag of de varianties in de populaties wel of niet verschillend zijn. Voordat men verder kan met de t-toets, moet men eerst toetsen met |
de F-toets of de varianties gelijk zijn.
|
|
|
Er zijn twee varianten van de t-toets voor het verschil tussen twee gemiddelden die samenhangen met de vraag of de varianties in de populaties wel of niet verschillend zijn.
De twee varianten: |
Variant 1: Toetsingsgrootheid als varianties gelijk zijn
Variant 2: Toetsingsgrootheid als varianties ongelijk zijn |
|
|
Variant 1: Toetsingsgrootheid als varianties gelijk zijn
|
Uitgaande van twee normaal verdeelde populaties met gelijke, doch onbekende varianties
(dus met σ(in het kwadraat) 1 = σ in het kwadraat 2 = σ in kwadraat), is de steekproevenverdeling van X1 - X2 een normale verdeling waarvan de verwachte waarde gelijk is aan μ1 - μ2. Met de variantie (of met de standaardafwijking) van deze verdeling is het iets ingewikkelder gesteld, want hiervoor moet eerst de populatievariantie σ2 worden geschat op basis van beide steekproefvarianties. Als de populatievarianties inderdaad gelijk zijn, kunnen we de populatievariantie ( σ 2) schatten als een gewogen gemiddelde van de twee steekproefvarianties. |
|
|
Met de variantie (of met de standaardafwijking) van deze verdeling is het iets ingewikkelder gesteld, want hiervoor moet eerst de populatievariantie σ2 worden geschat op basis van beide steekproefvarianties. Als de populatievarianties inderdaad gelijk zijn, kunnen we de populatievariantie ( σ2) schatten als een gewogen gemiddelde van de twee steekproefvarianties.
Dit heet in het Engels |

het 'poolen' van de steekproefvarianties. We doen dit met behulp van de volgende formule:
'Gepoolde' variantie op basis van twee steekproeven uit populaties met gelijke varianties |
|

We herkennen hierin
|

de vorm die we zo juist bij de variantie van de verdeling van het verschil tussen twee gemiddelde tegenkwamen toen we de varianties wél kenden.
|
|
|
Omdat we te maken hebben met een normale verdeling en een onbekende (immers geschatte) σ, gaan we weer over op de t-verdeling die voor dit soort situaties is ontwikkeld.
Het omzetten van het geobserveerde verschil X1 - X2 in een t-score geschiedt met de volgende formule: |

T-score voor het verschil in gemiddelden van twee steekproeven uit populaties met gelijke varianties
|
|
|
Ook hier weer, hoe groter het aantal vrijheidsgraden, hoe meer
|
De verdeling op een standaard normale verdeling gaat lijken.
|
|
|
Variant 2:
Toetsingsgrootheid als varianties ongelijk zijn Wanneer de populatievarianties ongelijk zijn, kan men het verschil tussen de geobserveerde steekproefgemiddelden X1 - X2 omzetten in de volgende geobserveerde t-score: |

t-score voor het verschil tussen twee steekproefgemiddelden bij populaties met ongelijke varianties.
Merk op, dat deze formule sterk lijkt op die van de z-score, met dien verstande dat de populatievarianties vervangen zijn door de steekproefvarianties. Het aantal vrijheidsgraden wordt echter een ingewikkelde functie. |
|
|
Merk op, dat deze formule sterk lijkt op die van de z-score, met dien verstande dat de populatievarianties vervangen zijn door de steekproefvarianties.
Het aantal vrijheidsgraden wordt echter een ingewikkelde functie. |

In feite wordt het aantal vrijheidsgraden nu geschat.
De toetsingsgrootheid volgt nu een t-verdeling met dit aantal vrijheidsgraden. |
|
|
Beslissingsregel
Ook nu kan de beslissing over het al of niet verwerpen van de H0 weer op twee manieren worden geformuleerd: |
met behulp van overschrijdingskansen
en met behulp van kritieke waarde(n) en kritieke zone(s) . Met behulp van overschrijdingskansen berekenen we eerst met behulp van een computerprogramma de overschrijdingskans van de toetsingsgrootheid onder de aanname dat de H0 juist is . De H0 wordt verworpen indien voor een bepaalde en een bepaald aantal vrijheidsgraden, of de linker, of de rechter of tweezijdig overschreden worden. |
|
|
Wanneer we de H0 toetsen met behulp van kritieke waarden, dan bepalen we eerst
|
welke t-waarde (n) hoort of horen bij het significantieniveau a en het aantal vrijheidsgraden.
|
|
|
Betrouwbaarheidsinterval
Als we met een bepaald percentage zekerheid willen weten binnen welke grenzen het verschil tussen twee populatiegemiddelden ligt, dan berekenen we een |
betrouwbaarheidsinterval.
|
|
|
Betrouwbaarheidsinterval als varianties gelijk zijn
Bij gelijke populatievarianties is de formule voor een 100(1 - α)%-betrouwbaarheidsinterval gelijk aan: |

|
|
|
Betrouwbaarheids interval als varianties ongelijk zijn
Bij ongelijke populatievarianties is de formule voor een 100(1 - a)%-betrouwbaarheidsinterval gelijk aan: |

|
|
|
De formules voor beide betrouwbaarheidsintervallen lijken sterk op elkaar.
Wanneer de populatievarianties gelijk zijn, komt in de formules voor de toetsingsgrootheid en het betrouwbaarheidsinterval de gepoolde variantie te staan; zijn de populatievarianties ongelijk, dan |
komen in de formules voor de toetsingsgrootheid en het betrouwbaarheidsinterval de afzonderlijke steekproefvarianties te staan .
|
|
|
Slotwoord t-toets voor het verschil tussen twee gemiddelden
Wat gebeurt er echter als we de toetsen met elkaar verwarren en we de t-toets voor ongelijke populatievarianties gebruiken wanneer de populatievarianties gelijk zijn aan elkaar? |
We krijgen dan minder snel een significant resultaat:
het onderscheidingsvermogen neemt af. Hoeveel het scheelt, hangt af van de steekproefgroottes en het verschil tussen de varianties. Bij grote steekproeven is het verschil tussen de twee t-toetsen klein. Bovendien is de verstorende invloed van de ongelijke varianties bij grotere steekproeven klein. |
|
|
Toets voor gepaarde waarnemingen: twee afhankelijke
steekproeven Toetsingssituatie De t-toets voor gepaarde waarnemingen heeft met de z-toets en de t-toets voor het verschil tussen twee gemiddelden gemeen dat |
de onderzoeker geïnteresseerd is in de verschillen tussen twee populntiegemiddelden.
Maar bij deze toetsen werden er twee onafhankelijke steekproeven getrokken: een element dat uit de ene populatie wordt getrokken zegt niets over welk element er uit de andere populatie zal worden getrokken. De t-toets voor gepaarde waarnemingen werkt met afhankelijke steekproeven. |
|
|
De t-toets voor gepaarde waarnemingen werkt met
|
afhankelijke steekproeven.
Wanneer men bij elk element in de eerste steekproef het identieke element zoekt uit de tweede populatie, is er sprake van herhaalde metingen. Men kan ook bij elk element in de eerste steekproef een element in de tweede populatie zoeken dat zo veel mogelijk lijkt op het reeds getrokken element; dat heet matchen. Zowel matchen als herhaalde metingen leiden tot afhankelijke steekproeven. |
|
|
Men kan ook bij elk element in de eerste steekproef een element in de tweede populatie zoeken dat zo veel mogelijk lijkt op het reeds getrokken element;
dat heet: |
matchen.
Zowel matchen als herhaalde metingen leiden tot afhankelijke steekproeven. |
|
|
De redenen om in een onderzoek met afhankelijke steekproeven te werken, zijn gelegen in
|
een grotere efficiëntie en nauwkeurigheid . In het
algemeen is dergelijk onderzoek goedkoper (men heeft minder proefpersonen nodig) en preciezer (het leidt tot nauwkeuriger metingen). Maar in lang niet alle onderzoekssituaties kunnen afhankelijke steekproeven worden gebruikt (zie Hoyle e.a. 2002, Turner & Thayer 2001). Dus net als in de twee vorige paragrafen blijft het doel om na te gaan of twee populatiegemiddelden van elkaar verschillen, maar voor de t-toets voor gepaarde waarnemingen gebruikt men afhankelijke steekproeven, bijvoorbeeld gematchte paren, natuurlijke paren of twee keer dezelfde groep respondenten. |
|
|
Wanneer wél t-toets met gepaarde waarneming?
Voorwaarden |
De t-toets voor gepaarde waarnemingen mag worden gebruikt wanneer:
-de steekproeven afhankelijk zijn; -we kleine steekproeven trekken uit populaties die -normaal verdeeld zijn met onbekende standaarddeviaties; -de steekproeven groter zijn dan 30 en het aantal paren dus 30 of meer bedraagt. |
|
|
Wanneer geen t-toets met gepaarde waarneming?
De t-toets voor gepaarde waarnemingen mag niet worden gebruikt wanneer: |
-de twee afhankelijke steekproeven klein zijn (n < 30) en de populaties niet normaal verdeeld zijn;
-de betreffende variabelen niet op een intervalschaal zijn gemeten . -Bij afhankelijke steekproeven komen dan de tekentoets en de rangtekentoets in aanmerking. |
|
|
Hypothesen
Als we met gematchte of natuurlijke paren willen nagaan of twee populatiegemiddelden van elkaar verschillen, bepalen we voor de twee steekproeven eerst het verschil per paar (v) en berekenen we vervolgens van deze verschillen het gemiddelde (V) en de standaarddeviatie μy. Als de nulhypothese dat er geen verschil is tussen de populatiegemiddelden juist is, dan is de verwachte waarde van het gemiddelde verschil gelijk aan: |
0.
Met andere woorden, we zien de verschillen binnen de paren als een steekproef uit een populatie waarvan we onder H0 verwachten dat μv = 0. |
|
|
Toetsingsgrootheid
Om de overschrijdingskans van het gemiddelde verschil (V) te kunnen berekenen, moet dit worden omgezet in een t-score. Deze t-score is de toetsingsgrootheid, omdat |
het de statistische grootheid is waarmee we nagaan of de H0 kan worden verworpen. De formule is:
|
|
|
Deze t-score is de toetsingsgrootheid, omdat het de statistische grootheid is waarmee we nagaan of de H0 kan worden verworpen. De formule is:
|

Als aan de voorwaarden voldaan is, volgt tv een t-verdeling met n - 1 vrijheidsgraden.
Als de H0 juist is, zal de geobserveerde tv-waarde ongeveer gelijk zijn aan 0. Naarmate de geobserveerde tv-score verder van 0 af ligt, wordt steeds minder aannemelijk dat de nulhypothese juist is. |
|
|
Beslissingsregel
Ook nu kan de beslissing over het al of niet verwerpen van de H0 op twee manieren worden geformuleerd: |
met behulp van overschrijdingskansen
en met behulp van kritieke waarde(n) en kritieke zone(s). Met behulp van overschrijdingskansen bepalen we eerst de overschrijdingskans van de toetsingsgrootheid onder de aanname dat de H0 juist is. De H0 wordt verworpen indien voor een bepaalde en een bepaald aantal vrijheidsgraden: |
|
|
Met behulp van overschrijdingskansen bepalen we eerst de overschrijdingskans van de toetsingsgrootheid onder de aanname dat de H0 juist is.
De H0 wordt verworpen indien voor een bepaalde en een bepaald aantal vrijheidsgraden: |
Dat kan gaan om linkseenzijdige toetseing, rechtseenzijdige toetsing of tweezijdige toetsing
|
|
|
Wanneer we de H0 toetsen met behulp van kritieke waarden, dan bepalen we eerst
|
welke t-waarde(n) hoort of horen bij het significantieniveau α en het aantal vrijheidsgraden.
|
|
|
Betrouwbaarheidsinterval
Als we het werkelijke verschil μv tussen twee populatiegemiddelden willen schatten, dan doen we dit met een betrouwbaarheidsinterval. De formule voor het 100(1 - a.)% betrouwbaarheidsinterval is: Het 100(1 - α)-betrouwbaarheidsinterval voor het gemiddelde verschil bij afhankelijke steekproeven is: |

Met 100(1 - α)% zekerheid weten we dan dat het verschil tussen de twee populatiegemiddelden tussen de twee genoemde grenzen van het interval ligt.
|
|
|
6.6 Toets voor twee varianties: de f-toets
Toetsingssituatie De centrale vraag bij de F-toets is |
of twee populatievarianties van elkaar verschillen.
Deze toets kan worden gebruikt om na te gaan of wordt voldaan aan de voorwaarden van gelijke varianties bij de t-toets voor gepoolde varianties uit paragraaf 6.4. |
|
|
De F-toets voor twee varianties komt erop neer dat
|
we de varianties s1 in het kwadraat en s2 in het kwadraat van de steekproeven bepalen en vervolgens nagaan hoeveel maal de grootste van de twee groter is dan de kleinste door de grootste variantie
te delen door de kleinste. Het quotiënt noemen we F. |
|
|
De F-toets om na te gaan of twee populatievarianties verschillen zou in de volgende situatie kunnen worden gebruikt.
Goedbedoelde ingrepen kunnen soms bij verschillende mensen anders uitpakken. Kinderen in de klas extra belonen als ze iets goed doen, werkt stimulerend. Maar voor slechtere kinderen betekent dit, dat ze veel minder worden beloond dan de andere kinderen die ze om zich heen zien en dat zou juist demotiverend kunnen werken. Als deze conclusie juist is, is het gevolg dat goede kinderen het beter gaan doen en slechtere kinderen nog slechter. Het gevolg hiervan is weer dat de spreiding van bijvoorbeeld cijfers groter wordt. In klassen waarin veel extra wordt beloond, moet |
de variantie dus groter zijn dan in klassen waarin
dit niet het geval is. |
|
|
Wanneer een F toets?
Voorwaarden De F-toets voor twee varianties mag worden gebruikt indien .. |
de populaties waaruit de steekproeven worden getrokken normaal verdeeld zijn.
Bij de F-toets luistert deze eis nauw. Bij kleine afwijkingen van de normale verdeling kan de F zeer veel afwijken van wat hij in werkelijkheid zou moeten zijn. Slechts bij grote steekproeven (11 > 100) worden de afwijkingen acceptabel. |
|
|
Toetsingsgrootheid
Als toetsingsgrootheid om de H0 te toetsen nemen we het quotiënt van de varianties van beide steekproeven. Steeds delen we daarbij door de kleinste variantie (die dus in de noemer komt); de grootste variantie zetten we in de teller. Dit quotiënt wordt aangeduid met de letter F van Fisher, de statisticus. |

Als de nulhypothese waar is, bestaat er geen verschil tussen de populatievarianties en zal F in de buurt liggen van 1.
Naarmate F groter is, is het aannemelijker dat de populatievarianties werkelijk van elkaar verschillen. |
|
|
Als de nulhypothese waar is, bestaat er geen verschil tussen de populatievarianties en zal F in de buurt liggen van 1.
Naarmate F groter is, is het aannemelijker dat de populatievarianties |
werkelijk van elkaar verschillen.
Als de H0 juist is, volgt de toetsingsgrootheid een kansverdeling die de F-verd eling wordt genoemd. De vorm van deze verdeling hangt via de vrijheidsgraden df1 en df2 uitsluitend af van de grootte van beide steekproeven, dus van n1 en n2. De vorm van deze F-verdeling is in zijn algemeenheid scheef naar rechts; F-verdeling is niet symmetrisch de F-verdeling is dus niet symmetrisch. Een voorbeeld van een F-verdeling is gegeven in figuur 6.1. |
|
|
De vorm van deze verdeling hangt via de vrijheidsgraden df1 en df2 uitsluitend af van
|
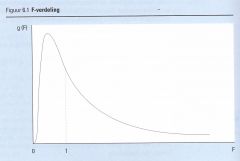
de grootte van beide steekproeven, dus van n1 en n2.
De vorm van deze F-verdeling is in zijn algemeenheid scheef naar rechts; F-verdeling is niet symmetrisch de F-verdeling is dus niet symmetrisch. Een voorbeeld van een F-verdeling is gegeven in figuur 6.1. |
|
|
Ook hier geven oppervlakten kansen op F-waarden weer tussen bepaalde waarden van F.
Omdat we echter slechts geïnteresseerd zijn in F-waarden met rechter overschrijdingskansen die gelijk zijn aan vaak voorkomende waarden van α, zijn alleen deze getabelleerd. Omdat elk paar vrijheidsgraden een andere F-verdeling inhoudt, bevat de tabel voor elke waarde van α ... |
een groot aantal verdelingen .
|
|
|
Beslissingsregel
Wederom kan de beslissingsregel op twee manieren worden geformuleerd: |
met behulp van overschrijdingskansen en met behulp van kritieke waarde(n) en zone(s)
|
|

Overschrijdingskansen
|

kritieke waarden
|
|
|
6.7 Toets voor de correlatie
Toetsingssituatie Om te toetsen of er een bepaald lineair verband aanwezig is in de populatie, gebruiken we |
de toets voor de correlatie.
Meestal gaat het om het verband tussen twee variabelen die zijn waargenomen bij dezelfde personen. Het kan echter ook gaan om de correlatie tussen dezelfde variabelen op verschillende tijdstippen of om de correlatie tussen dezelfde variabelen die gemeten zijn bij gematchte of natuurlijke paren. |
|
|
Voorbeelden van vragen waarin de toets voor de correlatie zou kunnen worden toegepast, zijn:
|
Hangt de intelligentie van schoolkinderen samen met de schoolprestatie voor taal?
Welke overeenkomst is er tussen ouders wanneer beiden de intelligentie van hun kinderen schatten? Hangt het aantal uren slaap dat kinderen uit groep 6 per nacht genieten samen met hun concentratie op school? Is er een verband tussen de mate waarin mensen aan zelfbeklag doen en hun assertiviteit? etc |
|
|
Om vast te stellen of er een verband is, trekken we een steekproef uit de populatie en bepalen van elk element (dus van elke persoon) de waarden op de twee variabelen waartussen we de samenhang willen bepalen en berekenen vervolgens
|
de correlatie.
|
|
|
Voorwaarden
De toets voor de correlatie mag worden toegepast, indien: |
1 de variabelen X en Y op intervalniveau zijn gemeten;
2 de variabelen X en Y een bivariaat-normale kansverdeling hebben; dit wil ruwweg zeggen dat de Y-waarden voor elke waarde van X normaal zijn verdeeld, en vice versa; 3 de populatievarianties van Y voor elke waarde van X gelijk zijn aan elkaar; de zogenaamde homoscedasticiteit. Er bestaan zelfs toetsen om na te gaan of aan deze voorwaarden is voldaan (zie Blalock 1972, Guilford 1973). In de praktijk zijn die toetsen echter niet altijd toepasbaar en gebruiken we doorgaans zonder meer de correlatietoets. |
|
|
Toetsingsgrootheid
De correlatie r die we in de steekproef hebben gevonden, moet worden omgezet in een t-score. Dit geschiedt met de volgende formule: |

T-score van een steekproefcorrelatie.
Mits aan de voorwaarden is voldaan, kan onder de aanname dat de nulhypothese juist is (en de populatiecorrelatie p dus gelijk is aan 0) worden aangetoond dat de steekproevenverdeling van r een t-verdeling volgt met df = n - 2 vrijheidsgraden. |
|
|
Beslissingregels
Met behulp van overschrijdingskansen bepalen we eerst de overschrijdingskans van de toetsingsgrootheid t, onder de aanname dat H0 juist is. De nulhypothese wordt verworpen indien: |

|
|
|
6 .8 Slotwoord parametrische toetsen
We hebben ons in het voorgaande tot de meest gebruikte parametrische toetsen voor één en twee steekproeven beperkt. Dat zijn uiteraard niet alle toetsen die er zijn . We noemen nog enkele voorbeelden van andere hypothesen die we kunnen toetsen: 1 Correlatietoets voor waarden die afwijken van 0 2 Toets voor het verschil tussen twee of meer correlaties in onafhankelijke steekproeven 3 Toets voor het verschil tussen correlaties bij afhankelijke steekproeven 4 CHi kwadraat-toets voor één variantie Deze toets gebruiken we als we willen nagaan of de variantie in een normaal verdeelde populatie een bepaalde waarde heeft, bijvoorbeeld als we willen nagaan of de steekproef afkomstig is uit een populatie waarin het IQ een standaardafwijking van 15 heeft . |
1 Correlatietoets voor waarden die afwijken van 0
Deze toets gebruiken we wanneer we ons afvragen of de populatiecorrelatie wel of niet een bepaalde waarde heeft. De meest voorkomende nulhypothese is dan: H0: p = p0 (p0 is een bepaalde van 0 afwijkende waarde). 2 Toets voor het verschil tussen twee of meer correlaties in onafhankelijke steekproeven Veronderstel dat we in twee of meer onafhankelij ke steekproeven de correlatie h ebben berekend tussen X en Y en na willen gaan of de overeenkomstige correlaties in de populaties waaruit de steekproeven komen verschillen. De nulhypothese is dan: H0: p 1= pz= ... = p11 3 Toets voor het verschil tussen correlaties bij afhankelijke steekproeven Hier gaat het om het verschil tussen correlaties binnen één en dezelfde steekproef, bijvoorbeeld het verschil in correlatie wanneer de variabelen X1 en X2 met een derde variabele X3 worden gecorreleerd. Dit geval doet zich met name voor als we twee validiteitcoëfficiënten willen vergelijken : twee tests correleren elk met eenzelfde criterium X3. Om na te gaan of er verschillen zijn, toetsen we meestal de nulhypothese: H0: p 13 = Pz3 4 CHi kwadraat-toets voor één variantie Deze toets gebruiken we als we willen nagaan of de variantie in een normaal verdeelde populatie een bepaalde waarde heeft, bijvoorbeeld als we willen nagaan of de steekproef afkomstig is uit een populatie waarin het IQ een standaardafwijking van 15 heeft . |
|
|
Hoe bepalen we welke toets we bij een bepaa lde vraagstelling moet gebruiken?
Welke van de genoemde parametrische, of de hierna te behandelen non-parametrische toet sen komt in aanmerking om de onderzoeksvraag te beantwoorden? Om deze vraag te kunnen beantwoorden moeten we allereerst |
nauwkeurig omschrijven wat de onderzoeksvraag is waarover we uitsluitsel willen, en in welke toetsingssituatie we ons bevinden.
|
|
|
Wat moeten we weten?
|
Aantal populaties
Hoeveel populaties zijn er in het geding? Gaat het om de waarde van een parameter binnen één populatie (bijvoorbeeld het gemiddelde μ of de correlatie tussen twee variabelen p), of gaat het om het verschil tussen twee populaties (bijvoorbeeld of ze een verschillend populatiegemiddelde hebben, of dat hun varianties ve rschillen)? Dit bepaalt namelijk of we met een één-steekproefprobleem of een twee-steekproevenprobleem te maken hebben. Meetniveau Is (of zijn) de variabele(n) gemeten op interva lniveau of hoger? Zijn ze gemeten op ordinaal niveau of lager, gebruik dan in ieder geval een non-parametrische techniek. Populatie normaal verdeeld? Zijn de populaties normaal verdeeld met bekende standaardafwij kingen, of niet? Dit bepaalt of we een z-toets of een t-toets mogen gebruiken. Zijn de populaties ni et normaal verdeeld, maar zijn de steekproeven voldoende groot om te mogen veronderstellen dat de steekproevenverdeling va n het gemiddelde bij benadering n ormaa l is verdeeld? In dat geval mogen we de t-toets gebruiken . Zijn de steekproeven echter te klein, gebruik dan een van de non-parametrische toetsen. Afhankelijke of onafhankelijke steekproeven Zijn de steekproeven die we in situaties van twee of meer populaties trekken afhankelijk of onafhankelijk? Zijn ze onafhankelijk getrokken, gebruik dan toetsen voor onafhan kelij ke steekproeven . Zijn ze afhankelijk getrokken, gebruik dan toetsen voor afhankelijke steekproeven. |

