![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
58 Cards in this Set
- Front
- Back
|
In steady flow |
Velocity is not a function of time |
|
|
In unsteady flow |
Velocity is a function of time |
|
|
In inviscud flow |
Fluid has no viscosity No energy loss from friction between molecules |
|
|
In viscous flow |
Fluid is viscous Has frictional losses |
|
|
Reynolds number in terms of rotational speed |
=rho x N x D^2 /mu As u = N D N is rotational speed and D the diameter of propeller |
|
|
Homogenous system |
Either has constant properties or properties vary continuously |
|
|
Heterogenous system d |
More than one homogenous system Phases separated by physical boundary or discontinuity |
|
|
Define isolated clise |
No mass or energy flow |
|
|
Define closed |
Energy flow but no mass flow |
|
|
Define open |
Define both mass and energy flow (by heat and work) |
|
|
Adiabatic |
No heat flow in or out |
|
|
5 properties of matter |
Volume, pressure, temp, internal energy, entropy |
|
|
3 derived properties |
Enthalpy H Helmholtz free energy A Gibbs free energy G |
|
|
Extensive property |
Depends on the amount |
|
|
Intensive property |
Doesn’t |
|
|
Z |
Thermodynamic variable Extensive |
|
|
Zm |
Molar property |
|
|
State function |
Difference between two values regardless of path |
|
|
Maxwell Relation |
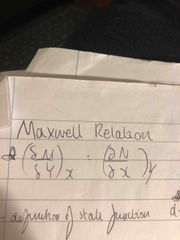
Back (Definition) |
|
|
State function definition |

Back (Definition) |
|
|
Use of Maxwell Relation |
To prove a function is a state function |
|
|
how to use Maxwells relation |
Let M equal what’s in front of do Let N equal what’s in front of dy Diff M in respect to Y with constant x Diff N in respect to X with constant y If values equal, sf |
|
|
U = |
= q + w |
|
|
Formula for heat, q |
= integral dq =integral C dT Where cp may equal a polynomial of T to integrate |
|
|
H = |
U + pV |
|
|
dq = For isochoric vs isobaric |
Isochoric =dU Isobaric = dH |
|
|
To demonstrate cv=(dq/dT)v =(dU/dt)v |
Use u=f(V,T) and dU=(dU/dV)T dv + (dU/dT)V dT Divide it by dT at a constant v Simplify as (dv/dt)v is 0 and (dT/dT)v is 1 |
|
|
Define 2nd law |
Entropy of universe increases to a max |
|
|
dU = (sf) |
dq + dw heat and work - not sf so not exact differentials |
|
|
Isochoric P V graph |
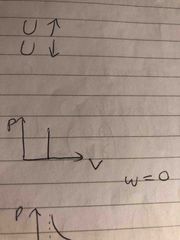
Constant volume |
|
|
Isothermal P V graph |
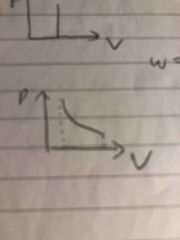
Back (Definition) |
|
|
Reversible work formula |

Back (Definition) |
|
|
Work done BY system |
Is negative |
|
|
For heat |
Signs are opposite |
|
|
Isochoric P V graph |
Constant volume |
|
|
To demonstrate cv=(dq/dT)v =(dU/dt)v |
Use u=f(V,T) and dU=(dU/dV)T dv + (dU/dT)V dT Divide it by dT at a constant v Simplify as (dv/dt)v is 0 and (dT/dT)v is 1 |
|
|
Reversible work formula |
Back (Definition) |
|
|
Kelli temp and calculating entropy change |

Back (Definition) |
|
|
Definition of fugacity |
Back (Definition) |
|
|
Reversible isothermal expansion of ideal gas And reversible adiabatic expansion |

Back (Definition) |
|
|
Unit of fugacity |
Same as pressure |
|
|
Fugacity co efficient |
Ratio f/p |
|
|
Chemical potential |

Back (Definition) |
|
|
Relationships |

Back (Definition) |
|
|
Vm is |
Gas molar volume |
|
|
Vm ideal is |
Molar volume of gas behaving ideally at same t and p |
|
|
De |
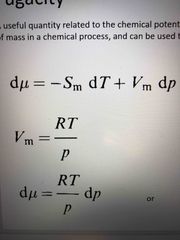
Back (Definition) |
|
|
Definition of fugacity |
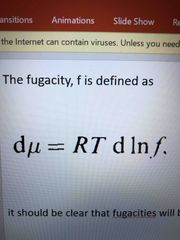
Back (Definition) |
|
|
f in terms of p |
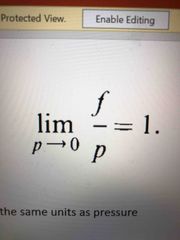
Back (Definition) |
|
|
Reversible isothermal expansion of ideal gas And reversible adiabatic expansion |
Back (Definition) |
|
|
Fugacity co efficient |
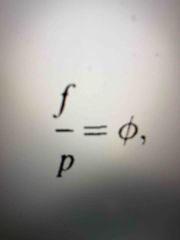
Ratio f/p |
|
|
To calculate delta U S H and G |
Find value in table Differentiate ideal eq and combine equations For G use other eq LOOK IN BOOK CH3 IF J BEVAN OTT J CHEMICAL THERMODYNAMIC PRINCIPLES AND APPLICATIONS |
|
|
Chemical potential |
Back (Definition) |
|
|
Relationships |
Back (Definition) |
|
|
Gibbs Phase rule |
f = c - p + 2 where c is no of independent components P is no of phases F is degree of freedom |
|
|
Fugacity |
measure of flow of mass in chemical process Can be used to determine point of equil |
|
|
Example of equation of state and alpha from data pVm = RT + Bp + cp^2 + Dp^3 ... |
Divide Vm by p Vm ideal = RT/p So calculate alpha |
|
|
Fugacity for pure condensed phases |
Back (Definition) |

