Mrc

Front 1

0.) Know ((closed book) how a test of any regression coefficient reflects a test of two models. Be able to take R2 values from a source (e.g. SPSS output) and compute an F-test AND/OR a t-test of a given variable’s contribution.

Back 1

One can test the significance of difference of two R2's to determine if adding an independent variable to the model helps significantly.

The hypothesis that a data set in a regression analysis follows the simpler of two proposed linear models that are nested within each other.

one often wants to determine whether model 2 gives a significantly better fit to the data. One approach to this problem is to use an F test.

Front 2

F-test

Back 2

Explained Variability/Unexplained Variability

Front 3

F-test RSS equation

Back 3

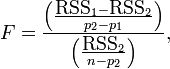
To determine whether model 2 gives a significantly better fit to the data. One approach to this problem is to use an F test.

'model 1 has p1 parameters, and model 2 has p2 parameters, where p2 > p1, and for any choice of parameters in model 1, the same regression curve can be achieved by some choice of the parameters of model 2.

y = mx + b has p = 2

F will have an F distribution, with (p2 − p1, n − p2) degrees of freedom. The null hypothesis is rejected if the F calculated from the data is greater than the critical value of the F distribution for some desired false-rejection probability (e.g. 0.05).

Front 4

how to test for the possibility of nonlinear components and product (“interaction?”) components in non-experimental research where the predictor variables are correlated.

Back 4

Centering the variables will move non-essential collinearity

Front 5

Interaction terms involving categorical dummies.

Back 5

To create an interaction term between a categorical variable and a continuous variable, first the categorical variable is dummy-coded, creating (k - 1) new variables, one for each level of the categorical variable except the omitted reference category. The continuous variable is mutliplied by each of the (k - 1) dummy variables. The terms entered into the regression include the continuous variable, the (k - 1) dummy variables, and the (k - 1) cross-product interaction terms. Also, a regression is run without the interaction terms. The R-squared difference measures the effect of the interaction.

Front 6

The significance of an interaction effect

Back 6

is the same as for any other variable, except in the case of a set of dummy variables representing a single ordinal variable. When an ordinal variable has been entered as a set of dummy variables, the interaction of another variable with the ordinal variable will involve multiple interaction terms. In this case the F-test of the significance of the interaction of the two variables is the significance of the change of R-square of the equation with the interaction terms and the equation without the set of terms associated with the ordinal variable.

Front 7

T-test

Back 7

are used to assess the significance of individual b coefficients. specifically testing the null hypothesis that the regression coefficient is zero. A common rule of thumb is to drop from the equation all variables not significant at the .05 level or better.

Front 8

Standard Error of Estimate (SEE),

Back 8

For large samples, SEE approximates the standard error of a predicted value. SEE is the standard deviation of the residuals. In a good model, SEE will be markedly less than the standard deviation of the dependent variable. In a good model, the mean of the dependent variable will be greater than 1.96 times SEE.

Front 9

F-test equation

Back 9

F = [R2/k]/[(1 - R2 )/(n - k - 1)]

Front 10

F-squared from SPSS

Back 10

F is the ratio of mean square for the model (labeled Regression) divided by mean square for error (labeled Residual), where the mean squarea are the respective sums of squares divided by the degrees of freedom.

Front 11

Calculate the F-value from the SPSS Output

Back 11

F = 16.129/2.294 = 7.031.

Front 12

Partial F test

Back 12

Partial-F can be used to assess the significance of the difference of two R2's for nested models. Nested means one is a subset of the other, as a model with interaction terms and one without. Also, unique effects of individual independents can be assessed by running a model with and without a given independent, then taking partial F to test the difference. In this way, partial F plays a critical role in the trial-and-error process of model-building.

Front 13

Calculating partial F

Back 13

Let there be q be a larger model and let p be a nested smaller model.
Let RSSp be the residual sum of squares (deviance) for the smaller model.
Let RSSq be the residual sum of squares for the larger model.
Partial F has df1 and df2 degress of freedom, where
df1 = df for RSSp minus RSSq
df2 = df of RSS in the larger model
Partial F = (RSSp - RSSq)/(df1*[RSSq/df2])

Front 14

R^2

Back 14

Also called multiple correlation or the coefficient of multiple determination, is the percent of the variance in the dependent explained uniquely or jointly by the independents

Front 15

R^2 calculation

Back 15

(1 - (SSE/SST)), where SSE = error sum of squares = SUM((Yi - EstYi)squared), where Yi is the actual value of Y for the ith case and EstYi is the regression prediction for the ith case; and where SST = total sum of squares = SUM((Yi - MeanY)squared).

Put another way, the regression sum of squares/total sum of squares = R-square, where the regression sum of squares = total sum of squares - residual sum of squares.

Front 16

R -sqd change

Back 16

R-sqd change, also called R-sqd increments, refers to the amount R-sqd increases or decreases when a variable is added to or deleted from the equation as is done in stepwise regression or if the researcher enters independent variables in blocks. If the "Enter" method is used to enter all independents at once in a single model, R-sqd change for that model will reflect change from the intercept-only model.

Front 17

R-sqd difference test

Back 17

refers to running regression for a full model and for the model minus one variable, then subtracting the R-sqd's and testing the significance of the difference.

Front 18

Stepwise

Back 18

ince stepwise regression adds one variable at a time to the regression model, generating an R2 value each time, subtracting each R2 from the prior one also gives the R2 increment. R2 increments are tested by the F-test and are intrinsic to hierarchical regression, discussed below.

Front 19

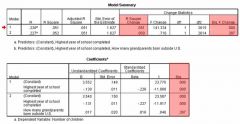
Interpret the model

Back 19

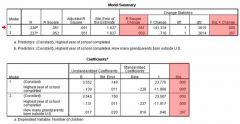
Choose model 1. # of grandparents born abroad does not add anything to the model. R^2 is significant at p<.001

Front 20

F-incremental

Back 20

[(R2with - R2without)/m] / [(1 - R2)/df]

Front 21

R2 change and dummy variables

Back 21

The incremental F test used with R2 change must be used to assess the significance of a set of dummy variables. Do not use individual t-tests of b coefficients of the dummy variables

Hint 21

where m = number of IVs in new block which is added; and df = N - k - 1 (where N is sample size; k is number of indpendent variables). F is read with m and df degrees of freedom to obtain a p (probability) value. Note the without model is nested within the with model.

Front 22

Squared semipartial (part) correlation:

Back 22

the proportion of total variance in a dependent variable explained uniquely by a given independent variable after other independnt variables in the model have been controlled. When the given independent variable is removed from the equation, R2 will be reduced by this amount. Likewise, it may be interpreted as the amount R2 will increase when that independent is added to the equation. R2 minus the sum of all squared semi-partial correlations is the variance explained jointly by all the independents (the "shared variance"of the model)

Front 23

Squared partial correlation:

Back 23

the proportion of variance explained uniquely by the given independent variable (after both the IV and the dependent have been adjusted to remove variance they share with other IVs) in the model. Thus the squared partial correlation coefficent is the percent of unexplained variance in the dependent which now can be accounted for when the given independent variable is added to the model.

Front 24

Use of residuals

Back 24

(1) to spot heteroscedasticity (ex., increasing error as the observed Y value increases),
(2) to spot outliers (influential cases), and
(3) to identify other patterns of error (ex., error associated with certain ranges of X variables)

Front 25

Outliers

Back 25

The removal of outliers from the data set under analysis can at times dramatically affect the performance of a regression model.

utliers should be removed if there is reason to believe that other variables not in the model explain why the outlier cases are unusual -- that is, outliers may well be cases which need a separate model. Alternatively, outliers may suggest that additional explanatory variables need to be brought into the model (that is, the model needs respecification).

Front 26

Unstandardized residuals,

Back 26

referenced as RESID in SPSS, refer in a regression context to the linear difference between the location of an observation (point) and the regression line (or plane or surface) in multidimensional space.

Front 27

Standardized residuals

Back 27

residuals after they have been constrained to a mean of zero and a standard deviation of 1. A rule of thumb is that outliers are points whose standardized residual is greater than 3.3 (corresponding to the .001 alpha level). SPSS will list "Std. Residual" if "casewise diagnostics" is requested under the Statistics button, as illustrated in the Casewise Diagnostics table below

Front 28

Studentized residuals

Back 28

are constrained only to have a standard deviation of 1, but are not constrained to a mean of 0.

Front 29

Partial regression plots, also called partial regression leverage plots or added variable plots,

Back 29

used to assess outliers and also to assess linearity. A partial regression plot is a scatterplot of the residuals of an independent variable on the x axis against the residuals of the dependent variable on the y axis, where the residuals are those obtained when the rest of the independent variables are used to predict the dependent and then the given independent variable separately. In the Chart Editor, the plots can be made to show cases by number or label instead of dots. The dots will approach being on a line if the given independent is linearly related to the dependent, controlling for other independents. Dots far from the line are outliers. The most influential outliers are far from the line in both x and y directions

Front 30

Multicollinearity

Back 30

the intercorrelation of independent variables.

the preferred method of assessing multicollinearity is to regress each independent on all the other independent variables in the equation

Inspection of the correlation matrix reveals only bivariate multicollinearity, with the typical criterion being bivariate correlations > .90. Note that a corollary is that very high standard errors of b coefficients is an indicator of multicollinearity in the data. To assess multivariate multicollinearity, one uses tolerance or VIF, which build in the regressing of each independent on all the others.

Front 31

Tolerance

Back 31

1 - R2 for the regression of that independent variable on all the other independents, ignoring the dependent. There will be as many tolerance coefficients as there are independents. The higher the intercorrelation of the independents, the more the tolerance will approach zero. As a rule of thumb, if tolerance is less than .20, a problem with multicollinearity is indicated.

Front 32

Variance-inflation factor, VIF VIF

Back 32

is the variance inflation factor, which is simply the reciprocal of tolerance

Standard error is doubled when VIF is 4.0 and tolerance is .25, corresponding to Rj = .87. Therefore VIF >= 4 is an arbitrary but common cut-off criterion for deciding when a given independent variable displays "too much" multicollinearity: values above 4 suggest a multicollinearity problem

Front 33

Condition indices and variance proportions.

Back 33

Condition indices are used to flag excessive collinearity in the data. A condition index over 30 suggests serious collinearity problems and an index over 15 indicates possible collinearity problems

Front 34

Stepwise multiple regression

Back 34

statistical regression, is a way of computing OLS regression in stages. In stage one, the independent best correlated with the dependent is included in the equation. In the second stage, the remaining independent with the highest partial correlation with the dependent, controlling for the first independent, is entered. This process is repeated, at each stage partialling for previously-entered independents, until the addition of a remaining independent does not increase R-squared by a significant amount (or until all variables are entered, of course). Alternatively, the process can work backward, starting with all variables and eliminating independents one at a time until the elimination of one makes a significant difference in R-squared.

Front 35

Hierarchical multiple regression (not to be confused with hierarchical linear models)

Back 35

similar to stepwise regression, but the researcher, not the computer, determines the order of entry of the variables. F-tests are used to compute the significance of each added variable (or set of variables) to the explanation reflected in R-square. This hierarchical procedure is an alternative to comparing betas for purposes of assessing the importance of the independents. In more complex forms of hierarchical regression, the model may involve a series of intermediate variables which are dependents with respect to some other independents, but are themselves independents with respect to the ultimate dependent. Hierarchical multiple regression may then involve a series of regressions for each intermediate as well as for the ultimate dependent.

Front 36

Caution on adding variables

Back 36

Adding variables to the model will always improve R2 at least a little for the current data, but it risks misspecification and does not necessarily improve R2 for other datasets examined later on. That is, it can overfit the regression model to noise in the current dataset and actually reduce the reliability of the model.

Front 37

Spuriousness

Back 37

The specification problem in regression is analogous to the problem of spuriousness in correlation, where a given bivariate correlation may be inflated because one has not yet introduced control variables into the model by way of partial correlation. For instance, regressing height on hair length will generate a significant b coefficient, but only when gender is left out of the model specification (women are shorter and tend to have longer hair).

Front 38

Suppression.

Back 38

Note that when the omitted variable has a suppressing effect, coefficients in the model may underestimate rather than overestimate the effect of those variables on the dependent. Suppression occurs when the omitted variable has a positive causal influence on the included independent and a negative influence on the included dependent (or vice versa), thereby masking the impact the independent would have on the dependent if the third variable did not exist.

Front 39

Proper specification of the model:

Back 39

If relevant variables are omitted from the model, the common variance they share with included variables may be wrongly attributed to those variables, and the error term is inflated. If causally irrelevant variables are included in the model, the common variance they share with included variables may be wrongly attributed to the irrelevant variables. The more the correlation of the irrelevant variable(s) with other independents, the greater the standard errors of the regression coefficients for these independents. Omission and irrelevancy can both affect substantially the size of the b and beta coefficients. This is one reason why it is better to use regression to compare the relative fit of two models rather than to seek to establish the validity of a single model.

Front 40

No overfitting

Back 40

Overfitting occurs when there are too many predictors in relation to sample size. The researcher adds variables to the equation while hoping that adding each significantly increases R-squared. However, there is a temptation to add too many variables just to increase R-squared by trivial amounts. Such overfitting trains the model to fit noise in the data rather than true underlying relationships. Overfitting may also occur for non-trivial increases in R-squared if sample size is small. Subsequent application of the model to other data may well see substantial drops in R-squared.

Front 41

Cross-validation

Back 41

a strategy to avoid overfitting. Under cross-validation, a sample (typically 60% to 80%) is taken for purposes of training the model, then the hold-out sample (the other 20% to 40%) is used to test the stability of R-squared. This may be done iteratively for each alternative model until stable results are achieved.

Front 42

Recursive Path Analysis Assumptions

Back 42

• Relations are linear, additive & causal.
• Each residual is uncorrelated with any
variable which precedes it in the model,
(i.e., No relevant variable is omitted).
• One-way causal flow.
• All measurements on an interval scale.
• No measurement error.

Front 43

Cause

Back 43

originates with the investigator, and comes from the nature of the data, not the statistical methods used.