Calc 2 Exam 2

Front 1

What are all the topics for exam 2?

Back 1

- Improper Integrals

- Areas Between Curves

- Volumes

- Volumes with Cylindrical Shells

- Arc Length

- Applications to Physics and Engineering

- Sequences

Front 2

What makes an improper integral divergent vs convergent?

Back 2

If it doesnt evaluate to a real number when you evaluate its limits its divergent, if it does evaluate to a real number its convergent

Front 3

How do you solve an improper integral problem?

Back 3

1. Solve the integral

2. Plug in the upper bound and the lower bound

3. If its limit evaluates to a real number then it is convergent, if it doesnt then its divergent

Front 4

Example 1 if an improper integral problem

Back 4

Front 5

Example 2 of an improper integral problem

Back 5

Front 6

Example 3 of an improper integral

Back 6

Front 7

What is the formula for the area between curves?

Back 7

f(x) - top/right function, g(x) - bottom/left function. Test which is which by plugging in values within the interval.

Front 8

What do you do when an area between curves problem that consists of 2 parts?

Back 8

1) find the point of intersection by making the functions equal to each other and then solving for x, this is how you know where the functions make the switch.

2) set up the intervals: upper bound <=> intersection point & intersection point <=> lower bound.

3) plug in values for these intervals to see which is on top and which is on bottom for both

4) set up 2 integrals for each region and add them together

Front 9

Example 1 of area between curves

Back 9

Front 10

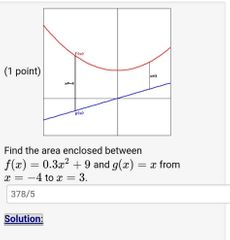
Example 2 of area between curves problem

Back 10

Front 11

Example 3 of area between curves problem

Back 11

Front 12

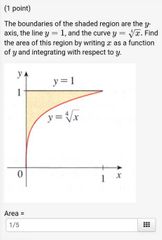
What is the equation for finding the volume of a shape found by rotating an area between functions?

Back 12

Front 13

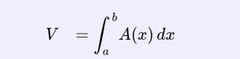
What does A(x) represent in the volume equation?

Back 13

Front 14

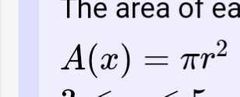
What is the equation for volume when there are two functions used as parameters for the area?

Back 14

Front 15

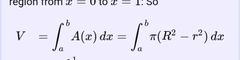
How do you solve an equation for volumes?

Back 15

1) determine which variable (x or y) the equation will be placed in

2) find the upper and lower bound of the integral, if in terms of x then this will be the range of the volume, if in terms of y then the domain of the area will be used

3) take the function(s) and plug it into the volume equation ( integral b/d <=> a/c pi(R^2 - r^2) dx/dy)

* if in y terms then R is the the rightmost functuon, if in x then R is the top function

4) solve the integral

Front 16

How can you tell which terms a volume problem will be in?

Back 16

If "about the y-axis" in terms of y

If "about the x-axis" in terms of x

Front 17

Example 1 of volumes problem

Back 17

Front 18

Example 2 of Volumes

Back 18

Front 19

If the volume is rotated around something bigger than the x-axis or the y-axis then what must you do?

Back 19

Modify the integral equation to Subtract both radiuses from whatever the value is that its rotating around

Front 20

Example 3 of volumes problem

Back 20

Front 21

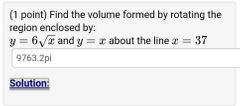
How do you find the volume of a circular disc?

Back 21

1) determine the radius and plug it into the equation for a circle: x^2 + y^2 = r^2

2) solve for y and then multiple by 2

3) plug it into an integral with the upper bound = r and the lower = -r

Front 22

How do you find the volume of a frustrum of a pyramid?

Back 22

...

Front 23

How do you find the volume of a frustrum of a right circular cone?

Back 23

...

Front 24

What is the equation for finding the volume using the cylindrical shell method?

Back 24

Front 25

What is the equation for finding the volume using the cylindrical shell method?

Back 25

Front 26

Example 1 of volume with cylindrical shell problem:

Back 26

Front 27

Example 2 of volumes using cylindrical shells problem

Back 27

Front 28

Example 3 of volume using cylindrical shells problem

Back 28

Front 29

How do you solve an arc length problem?

Back 29

1) determine the domain (if in terms if x) or range (if in y) to find the upper and lower bound of the integral and the derivative of the curve

2) plug these into the arc length equation and solve

Front 30

Example 1 of an arc length equation

Back 30

Front 31

Example 2 of an arc length problem

Back 31

Front 32

Example 3 of an arc length problem

Back 32

Front 33

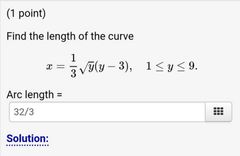
What is the formula to find work?

Back 33

Force × distance

Front 34

What is the formula for force?

Back 34

Mass × acceleration

Front 35

What is Hookes law?

Back 35

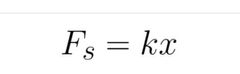
K = a constant when you divide the specific amount of force by a specific amount of stretch or compression

Front 36

What are equations youll potentially need for mass problems

Back 36

Force = mass × acceleration

Mass = density × volume

Acceleration is usually 9.8 m/s^2

Volume will depend on shapes in problem

Front 37

Example 1 of a physics application problem

Back 37

Front 38

Example 2 of a physics application problem

Back 38

Front 39

Example 3 of a physics application problem,

Back 39

Front 40

What is a sequence?

Back 40

A series of numbers that follow a formula

Front 41

How do you solve a sequence problem?

Back 41

Either find a pattern if the problem asks for one or evaluate the sequence like it is a limit to see if it converges. Divide by the largest degree in the denominator and evaluate each term to infinity