Linear Algebra

Front 1

direct sum

Back 1

Front 2

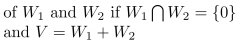
vector space

Back 2

addition: commutative, associative, identity, inverse

scalar multiplication: identity, (ab)x = a(bx)

distributive: (a + b)x = ax + bx; a(x + y) = ax + ay

Front 3

subspace

Back 3

contains 0 vector, closed under addition and scalar multiplication

Front 4

Theorem 1.4: Any intersection of subspaces..

Back 4

or a vector space V is a subspace of V.

Front 5

coset of W containing v

Back 5

{v} + W = {v + w: w in W}

Front 6

Theorem 1.5: The span of any subset S of a vector space V

Back 6

is a subspace of V. Moreover, any subspace of V that contains S must also contain the span of S.

Front 7

Back 7

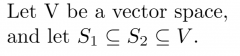
If S1 is linearly dependent, then S2 is linearly dependent.

If S2 is linearly independent, then S1 is linearly independent.

Front 8

Theorem 1.7: Let S be a linearly independent subset of a vector space V, and let v be in V but not in S...

Back 8

Then S U {v} is linearly dependent iff v is in span(S).

Front 9

Theorem 1.8: Let V be a vector space and beta = {u1, u2,..., un} be a subset of V. Then beta is a basis iff

Back 9

each v in V can be uniquely expressed as a linear combo of vectors of beta.

Front 10

Theorem 1.9: If a vector space is generated by a finite set S, then...

Back 10

some subset of S is a basis for V. Hence V has a finite basis.

Front 11

Theorem 1.10 (Replacement Theorem): Let V be a vector space generated by a set G containing n vectors, and let L be a lin. ind. subset of V containing m vectors...

Back 11

Then m <= n, and there exists a subset H of G containing n - m vectors such that L U H generates V.

Front 12

Theorem 1.10 Corollary 1: Let V be a vector space having a finite basis. Then...

Back 12

every basis for V contains the same number of vectors.

Front 13

Theorem 1.10 Corollary 2: Let V be a vector space with dimension n..

Back 13

a) Any finite generating set for V contains at least n vectors, and a generating set for V that contains exactly n vectors is a basis for V.

b) Any linearly ind. subset of V that contains exactly n vectors is a basis for V.

c) Every linearly ind. subset of V can be extended to a basis for V.

Front 14

Theorem 1.11: Let W be a subspace of a finite-dimensional vector space V.

Back 14

Then W is finite-dimensional, and dimW <= dimV. Moreover, if dim(W) = dim(V), then V = W.

Front 15

Theorem 1.11 Corollary: If W is a subspace of a finite-dimensional vector space V, then any basis for W...

Back 15

can be extended to a basis for V.

Front 16

maximal

Back 16

Let F be a family of sets. A member of F is called maximal if M is contained in no member of F other than M itself

Front 17

Maximal Principle.

Back 17

Let F be a family of sets. If, for each chain C in F, there exists a member of F that contains each member of C, then F contains a maximal member.

Front 18

Theorem 1.12: Let V be a vector space and S a subset that generates V.

Back 18

If beta is a maximal lin. ind. subset of S, then beta is a basis for V.

Front 19

Theorem 1.13: Let S be lin. ind. subset of a vector space V. Then there exists...

Back 19

a maximal lin. ind. subset of V that contains S.

Front 20

Linear transformation

Back 20

T(x + y) = T(x) + T(y)

T(cx) = cT(x)

Front 21

Theorem 2.1: Let V and W be vector spaces and T: V -> W be linear...

Back 21

N(T) and R(T) are subspaces of V and W, respectively.

Front 22

Theorem 2.2: Let V and W be vector spaces and T: V -> W be linear. If beta = {v1, v2, ..., vn} is a basis for V, then...

Back 22

R(T) = span(T(beta)) = span({T(v1), T(v2), ..., T(vn)})

Front 23

Theorem 2.3 (Dimension Theorem)

Back 23

if V is finite dimensional, then nullity(T) + rank(T) = dim(V).

Front 24

Theorem 2.4: T is one-to-one

Back 24

iff N(T) = {0}

Front 25

Theorem 2.5: dim(V) = dim(W) (finite)

Back 25

T is one-one <=> T is onto <=> rank(T) = dim(V)

Front 26

Theorem 2.6: {v1, v2, ..., vn} is a basis for V. For w1, w2, ..., wn in W...

Back 26

there exists exactly one linear transformation T: V -> W such that T(vi) = wi for i = 1, 2, ..., n.

Front 27

Theorem 2.6 Corollary: V has finite basis {v1, v2, ..., vn}. If U, T: V -> W are linear and U(vi) = T(vi) for i = 1, 2, ..., n...

Back 27

U = T

Front 28

T-invariant

Back 28

T: V -> V is linear. Subspace W of V is T-invariant if T(x) \in W for every x in W.

Front 29

L(V, W)

Back 29

vector space of all linear transformations from V into W..

Front 30

Theorem 2.8: Let V and W be finite-dimensional vector spaces with ordered bases beta and gamma, and let T, U: V -> W be linear. Then...

Back 30

Front 31

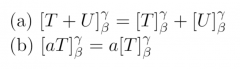
Theorem 2.9: Let V, W, and Z be vector spaces o ver the same field F, and let T: V -> W and U: W -> Z be linear.

Back 31

Then UT: V -> Z is linear.

Front 32

Theorem 2.10. Let V be a vector space. Let T, U1, U2 be in L(V). Then.

Back 32

Front 33

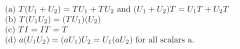
The V, W, and Z be finite-dimensional vector spaces with ordered bases alpha, beta, and gamma. Let T: V --> W and U: W -> Z be linear transformations. Then...

Back 33

Front 34

Corollary to Theorem 2.11: Let V be a finite-dimensional vector space with an ordered bais beta. Let T, U be in L(V). Then...

Back 34

Front 35

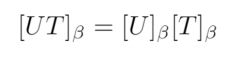
Theorem 2.14: Let V and W be finite-dimensional vector spaces having ordered bases beta and gamma, and let T: V -> W be linear. Then for each u in V we have...

Back 35

Front 36

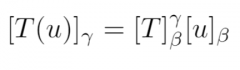
Theorem 2.15: Let A be m x n (F). Then the left-multiplication transformation is linear. B is any other m x n matrix, beta and gamma standard ordered bases for Fn and Fm...

Back 36

Front 37

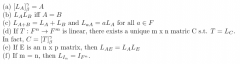
facts for invertible functions T and U

Back 37

Front 38

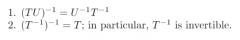
Theorem 2.17: Let V and W be vector spaces, and let T: V -> W be linear and invertible...

Back 38

Then inverse of T: W -> V is linear.

Front 39

Lemma on page 101. Let T be an invertible linear transformation from V to W.

Back 39

Then V is finite-dimensional iff W is finite-dimensional. Then dim(V) = dim(W).

Front 40

Theorem 2.18: Let V and W be finite-dimensional vector spaces with ordered bases beta and gamma. Let T: V -> W be linear. Then T is invertible iff

Back 40

Front 41

Corollary 2, Thm 2.18: Let A be an n x n matrix. Then A is invertible iff

Back 41

Front 42

Theorem 2.19. Let V and W be finite-dimensional vector spaces. Then V is isomorphic to W iff

Back 42

dim(V) = dim(W)

Front 43

Theorem 2.20: Let V and W be finite-dimensional vector spaces over F of dimensions n and m, and let beta and gamma be ordered bases. The function phi

Back 43

Front 44

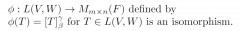
Corollary to 2.20: Let V and W be finite-dimensional vector spaces of dimensions n and m. The L(V, W)

Back 44

is finite-dimensional of dimension mn.

Front 45

standard representation of V with respect to beta

Back 45

Front 46

Back 46

Front 47

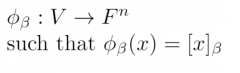
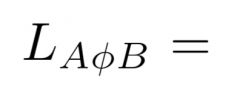
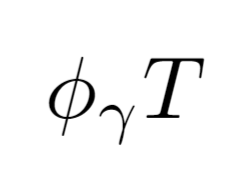
Theorem 2.22: Let beta and beta' be two ordered bases for a finite-dimensional vector space V, and let Q =

Back 47

Front 48

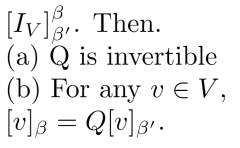
linear operator

Back 48

linear transformation that map a vector space into itself

Front 49

Theorem 2.23: Let T be a linear operator on a finite-dimensional vector space V, and let beta and beta' be ordered bases for V. Suppose Q is the change of coordinate matrix that changes beta'-coordinates into beta-coordinates. Then...

Back 49

Front 50

B is similar to A if

Back 50

there exists an invertible matrix Q such that B = Q^-1AQ