![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
7 Cards in this Set
- Front
- Back

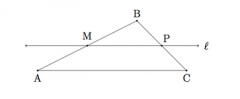
Given triangle ABC, where M is the midpoint of AB and l is the line through M, parallel to AC, show that angle CAB is congruent to angle PMB and that angle BPM is congruent to angle BCA. Conclude that triangle MBP is similar to triangle ABC.
|

After drawing two additional points, D and E on l outside of M and P, respectively, we can conclude that angle CAB is congruent to angle DMA because they are alternate interior angles. Angle DMA is congruent to angle PMB because they are vertical angles; therefore, angle CAB is congruent to angle PMB. Angle BCA is congruent to angle EPC because they are alternate interior angles, and angle EPC is congruent to angle BPM by vertical angles, therefore angle BCA is congruent to BPM. Triangles ABC and MBP share 3 congruent angles and therefore are similar triangles.
|
|
Given triangle ABC, where M is the midpoint of AB and l is the line through M, parallel to AC, and the information from the previous problem, show that P is the midpoint of BC.
|
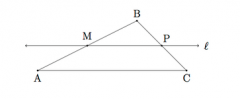
Since triangles MBP and ABC are similar, it follows that |PB|/|CB|=|BM|/|BA|. Since M is the midpoint of BA, we have |BM|/|BA|=1/2 and so |PB|/|CB|=1/2 which means that P is the midpoint of segment CB.
|
|
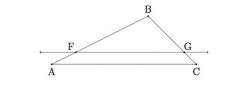
Given triangle ABC, where F is a point on AB and G is a point on BC so that |FA|/|AB|=|GC|/|BC|, show that FG is parallel to AC.
|
Since |FA|/|AB|=|GC|/|BC|, F and G must be the same vertical distance from AC if measured with a line perpendicular to AC. Since both points are the same distance away from AC and the line segment connects the two points with a straight line, it must be parallel to AC.
|
|
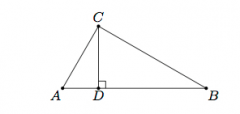
Given this figure with right triangle ABC and point D so that CD is perpendicular to AB, show that triangle ABC is similar to triangle ADC and triangle CDB.
|
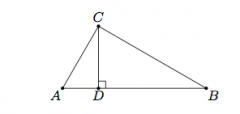
we know that m∠ACB=m∠CDA and m∠CAB=m∠DAC. Therefore, by AA similarity, triangle ACB is similar to triangle ADC. Alternatively, ∠DCA is complementary to ∠DAC and ∠CBA is complementary to ∠CAB. Angles complementary to congruent angles must be congruent so ∠DCA is congruent to ∠CBA. By AAA similarity, triangle ACB is similar to triangle ADC. Similar reasoning shows that triangle ACB is simliar to triangle CDB.
|
|
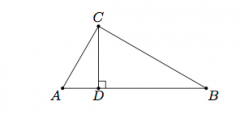
Given this figure with right triangle ABC and point D so that CD is perpendicular to AB, as well as the information from the previous part of this problem, conclude that |AC|²+|BC|²=|AB|².
|
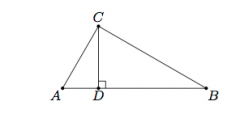
The two triangle similarity results from the previous part of this problem allow us to set up different proportions involving corresponding sides in the similar triangles. With two pairs of similar triangles (three if we include the fact that triangle ADC is similar to triangle DCB since both are similar to triangle ACB) this gives us six possible proportions. Some care is needed in order to choose the ones which will give the Pythagorean theorem. Suppose we choose |BC| and |AC| for a and b and |AB| for c. In order to get an a2 we would like to use the two occurences of BC, one in triangle ACB and one in triangle CDB so that a/c=|BD|/a. Simlarly, we can find b with b/c=|AD|/b. clearing denominators in our two fraction equivalences gives us a²=c|BD| and b²=c|AD|. Adding these together gives us a²+b²=c(|BD|+|AD|)=c|AB|=c².
|
|
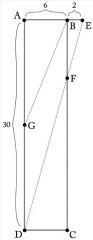
In rectangle ABCD, |AB|=6, |AD|=30, and G is the midpoint of AD. Segment AB is extended 2 units beyond B to point E, and F is the intersection of ED and BC. Given is a diagram that will be helpful in solving this problem. What is the area of BFDG?
|
By the AA criterion for similarity, triangle EBF is similar to triangle EAD. Since corresponding sides of similar triangles are proportional to one another, we can conclude that |BF|/|AD|=|BE|/|AE| and therefore |BF|/30=2/8. We conclude that BF=15/2 by cross multiplication. Segments BF and DG belong to opposite sides of rectangle ABCD which are parallel and so BDFG is a trapezoid. 1/2h(b₁+b₂)=1/2*|AB|*(|BF|+|GD|)=1/2*6*(15/2+15)=135/2
|
|
|
Suppose ABCD and EFGH are two parallelograms all of whose corresponding sides are congruent, that is |AB|=|EF|, |BC|=|FG|, |CD|=|GH|, and |DA|=|HE|. Is it always true that ABCD is congruent to EFGH?
|
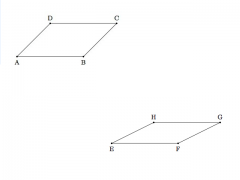
Begin by drawing or building a parallelogram. The opposite sides of a parallelogram are congruent so we will need two pairs of congruent segments. Now, if we imagine leaving segment AB fixed and "pushing down" on side CD so that these two sides become closer while side AD and BC rotate clockwise, we get a new parallelogram (EFGH). These two parallelograms have 4 congruent sides but they are not congruent since they have different angles and areas.
|

