High School Common Core Mathematics

Front 1

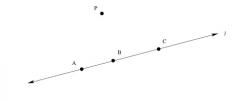
Suppose we apply a dilation by a factor of 2, centered at the point P, to the figure below. Part 1: locate the images A', B' and C', of the points A, B and C under this dilation.

Back 1

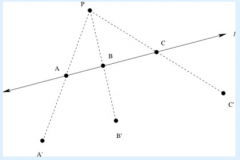
To locate the point A' , we draw a line segment from P to A, and extend the segment through A. We place A' on this line so that the distance from P to A' is twice the distance from P to A. We locate B' and C' using the same procedure.

Front 2

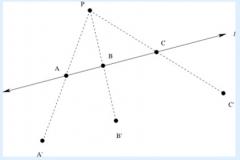
Suppose we apply a dilation by a factor of 2, centered at the point P, to the figure below. Part 2: Based on your picture from part 1, what do you think happens to the line l when we perform the dilation?

Back 2

The points A', B' and C' appear to be collinear. If we choose more points on l and dilate those points about P, we will see that the dilations of those points also appear to line on the line through A', B' and C'. It appears that the dilations of the points on the line l form a new line l' that is parallel to line l.

Front 3

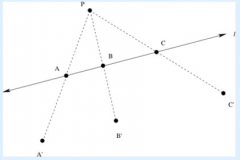
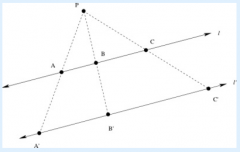
Suppose we apply a dilation by a factor of 2, centered at the point P, to the figure below. Part 3: Based on your picture in part 1, what appears to be the relationship between the distance A'B' and the distance AB? How about the distances B'C' and BC?

Back 3

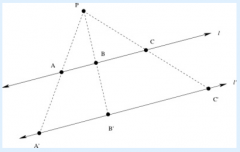
In the picture, it appears that A'B'=2AB, and B'C'=2BC. We can obtain more evidence for this guess by measuring the lengths of the segments in our picture.

Front 4

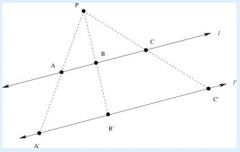
Suppose we apply a dilation by a factor of 2, centered at the point P, to the figure below. Part 4: Can you prove your observations from part 3?

Back 4

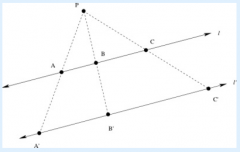
We will prove that A'B'=2AB; the proof that B'C'=2BC is very similar. Note that we will prove this fact without using our unproven conjecture that l' is parallel to l. Draw a line through A parallel to line PB, and a line through B parallel to line PA. Let these lines meet at X. Since PAXB is a parallelogram, we know that AX=PB, BX=PA and angle AXB is congruent to angle PBA. Now we turn our attention to triangle AA'X. We know that angle A'Ax is contruent to angle PAB. Thus, the angle AXA' is congruent to angle PBA. A similar arguement shows that triangle BXB' is congruent to triangle PAB and therefore angle BXB' is congruent to angle PAB. Now we know that m∠A'XA +m∠AXB+m∠BXB' = m∠PAB+ m∠APB+m∠PBA = 180°. Thus the angle A'XB' is a straight angle, and we now know that X lies on the line A'B'. The congruence of triangles PAB, AA'X and BXB' shows that AB=A'X=XB'. Since X lines on line A'B', we know that A'B'= A'X+XB' = AB+AB = 2AB.

Front 5

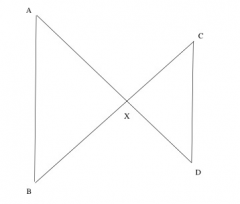
Determine whether the given assumptions are enough to prove that the two triangles are similar; and if so, what the correct correspondence of vertices is. If the two triangles must be similar, prove this result by describing a sequence of similarity transformations that maps one triangle to the other. If not, explain why not. GIVEN: line segments AD and BC intersect at X. Line segments AB and CD are drawn, forming two triangles AXB and CXD. The lengths AX and XD satisfy the equation 2AX=3XD

Back 5

This is not enough information to prove similarity. To see that in a simple way draw an arbitrary triangle AXB. Extend AX and choose a point D on the extended line so that 2AX=3XD. Extend BX and choose a point C on the extended lien so that 2BX=XC. Now triangles AXB and CXD satisfy the given conditions but are not similar.

Front 6

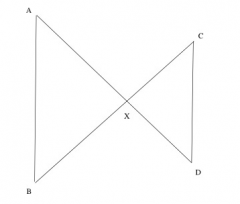
Determine whether the given assumptions are enough to prove that the two triangles are similar; and if so, what the correct correspondence of vertices is. If the two triangles must be similar, prove this result by describing a sequence of similarity transformations that maps one triangle to the other. If not, explain why not. GIVEN: line segments AD and BC intersect at X. Line segments AB and CD are drawn, forming two triangles AXB and CXD. The lengths AX, BX, CX, and DX satisfy the equation AX/BX=DX/CX.

Back 6

Rearranging the given proportion gives AX/DX=BX/CX let k=AX/DX. Suppose we rotate the triangle DXC 180 degrees about point X: since AD is a straight line, DX and AX align upon rotation of 180 degrees, as do CX and BX, and so angles DXC and AXB coincide after this rotation. Then dilate the trangle DXC by a factor of k about the center X. This dilation moves the point D to A since k(DX)=AX, and moves C to B, since k(CX)=BX. Then since the dilation files X, and dilations take line segments to line segments, we see that the triangle DXC is mapped to triangle AXB, so the original triangle DXC is similar to AXB.

Front 7

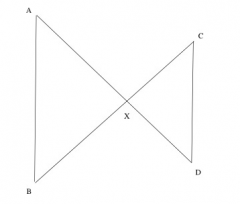
Determine whether the given assumptions are enough to prove that the two triangles are similar; and if so, what the correct correspondence of vertices is. If the two triangles must be similar, prove this result by describing a sequence of similarity transformations that maps one triangle to the other. If not, explain why not. GIVEN: line segments AD and BC intersect at X. Line segments AB and CD are drawn, forming two triangles AXB and CXD. Lines AB and CD are parallel.

Back 7

Rotate triangle DXC so that angle DXC coincides with angle AXB. Then the image of side CD under this rotation is parallel to the original side CD, so the new side CD is still parallel to side AB. Now, apply a dilation about point X that moves the vertex C to point B. This dilation moves the line CD to a line through B parallel to the previous line CD. We already know that the line AB is parallel to CD, so the dilation must move the line CD onto the line AB. Since the dilation moves D to a point on the ray XA and on the line AB, D must move to A. Therefore, the rotation and dilation map the triangle DXC to the triangle AXB. Thus, DXC is similar to AXB.

Front 8

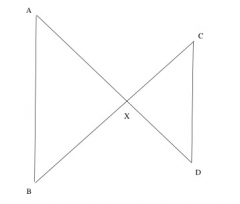
Determine whether the given assumptions are enough to prove that the two triangles are similar; and if so, what the correct correspondence of vertices is. If the two triangles must be similar, prove this result by describing a sequence of similarity transformations that maps one triangle to the other. If not, explain why not. GIVEN: line segments AD and BC intersect at X. Line segments AB and CD are drawn, forming two triangles AXB and CXD. Angle XAB is congruent to angle XCD.

Back 8

Suppose we draw the bisector of angle AXC, and reflect the triangle CXD across the angle bisector. This maps segment XC onto the segment XA; and since reflections preseve angles, it also maps segment XD onto segment XB. Since angle XCD is congruent to angle XAB, we also know that the image of side CD is parallel to side AB. Therefore, if we apply a dilation about the point X that takes the new point C to A, then the new line CD will be mapped onto the line AB. Therefore new point D is mapped to B, and thus the triangle XCD is mapped to trangle XAB. So triangle XCD is similar to triangle XAB.

Front 9

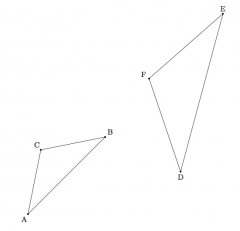
In these two triangles, m∠A=m∠D and m∠B=m∠E. Using a sequence of translation, rotation, reflections and/or dilations, show that ∆ABC is similar to ∆DEF.

Back 9

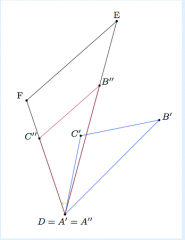
Step 1: Translation taking A to D
Step 2: Rotation of ∆A'B'C' by angle C'A'F
Step 3: Dilation centered at D by a factor of |DE|/|A"B"|