![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
12 Cards in this Set
- Front
- Back
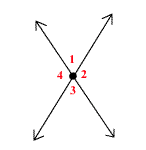
Given this diagram, prove that vertical angles are congruent.
|
Angles 1 and 3 are vertical angles.
∠1 and ∠2 form a linear pair, so they are supplementary. m∠1 + m∠2= 180°. ∠2 and ∠3 also form a linear pair, so m∠2 +m∠3= 180° This means that m∠1 + m∠2 = m∠2 + m∠3. Subtracting m∠2 from both sides of the the equation, we get m∠1=m∠3 |
|
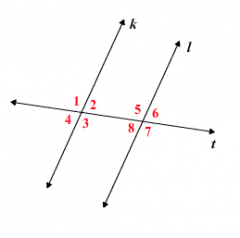
Given this diagram where k ‖ l, prove that alternate interior angles are congruent.
|
Angles 2 and 8 are alternate interior angles.
Since k ‖ l, by the Corresponding Angles Postulate, ∠1 ≅ ∠5. Therefore, by the definition of congruent angles, m∠1 = m∠5. Since ∠1 and ∠2 form a linear pair, they are supplementary, so, m∠1 + m∠2 = 180°. Also, ∠5 and ∠8 are supplementary, so m∠5 + m∠8 = 180°. Substituting m∠1 for m∠5, we get m∠1 + m∠8= 180°. Therefore, m∠1 + m∠2 = m∠1 + m∠8. Subtracting m∠1 from both sides we have m∠8 = m∠2. Therefore, ∠2 ≅ ∠8. |
|
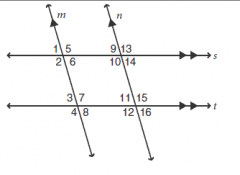
Name all the pairs of corresponding angles in this diagram.
|
1 and 9
2 and 10 3 and 11 4 and 12 5 and 13 6 and 14 7 and 15 8 and 16 |
|
|
Prove the Perpendicular Bisector Theorem, that if a point is equidistant from the endpoints of a segment then it is on the perpendicular bisector of that segment.
|

If AP ≅ BP, then P is on the perpendicular bisector of AB. Let M be the midpoint of AB. Now, ∆AMP ≅ ∆BMP by the side-side-side postulate. Therefore, ∠AMP ≅ ∠BMP since these are corresponding parts of congruent triangles. But these angles are a linear pair, so their measures add up to 180°. Since they are congruent angles, each must measure half of 180°, which is 90°. Therefore, PM ⊥ AB. So P is on the perpendicular bisector of AB.
|
|
|
Prove that the measures of interior angles of a triangle always sum to 180°.
|
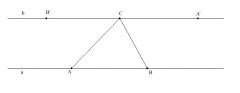
In this diagram, lines a and b are parallel. Since these lines are parallel, ∠BAC = ∠B'CA and ∠ABC=∠BCA'. Since the three angles form a striaght line, ∠B'CA+∠ACB+∠BCA'=180°. By substitution, ∠ABC+∠BCA+∠CAB=180°.
|
|
|
Prove that base angles of an isoceles triangle are always congruent using a 2 column- proof.
|
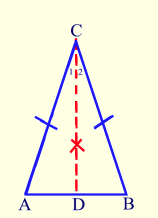
1. AC ≅ BC
1. Given 2.Draw CD bisecting ∠ACB 2. Each angle has one unique angle bisector. 3. ∠1 ≅ ∠2 3. An angle bisector is a ray whose endpoint is the vertex of the angle and which divides the angle into two congruent angles. 4. CD ≅ CD 4. Reflexive Property (A quantity is congruent to itself) 5. ∆ACD ≅ ∆BCD 5. SAS- if two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent. 6. ∠A ≅ ∠B 6. Corresponding parts of congruent triangles are congruent. |
|
|
prove that the segment joining midpoints of two sides of a triangle is parallel to the third side of a the triangle and is half the length of the third side.
|
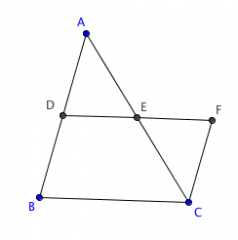
Let AD=BD and AE=CE. Extend DE beyond E to F such that DE=EF. Since AE=CE, triangles ADE and CEF are equal, making CF ‖ AB (or CF ‖ BD) because, for the transversal AC, the alternating angles DAE and ECF are equal. Also, CF=AD=BD, such that BDFC is a parallelogram, meaning DE ‖ BC. It follows that BC=DF=2DE.
|
|
|
Prove that the medians of a triangle meet at a point using a two-column proof.
|
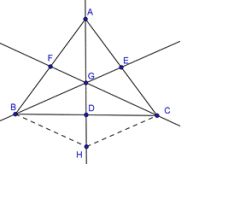
1. Point F is a midpoint of AB
1. By construction 2. Point E is a midpoint of AC 2. By construction 3. Draw BE 3. By construction 4. Draw FC 4. By construction 5. Point G is the point of intersection between BE and FC 5. Intersecting lines postulate 6. Draw AG 6. By Construction 7. Point D is the point of intersection between AG and BC 7. Intersecting lines Postulate 8. Point H lines on AG such that AG ≅ GH 8. By construction 9. FG ‖ BH and GE ‖ HC 9. Midsegment Theorem 10. GC ‖ BH and BG ‖ HC 10. Substitution 11. BCGH is a parallelogram 11. Properties of a parallelogram (opposite sides are parallel) 12. BD ≅ DC 12. Properties of a parallelogram (diagonals bisect each other ) |
|
|
prove that opposite sides of a parallelogram are congruent using a two-column proof.
|
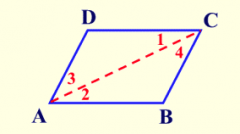
1. Parallelogram ABCD
1. Given 2. Draw segment from A to C 2. Two points determine exactly one line. 3. AB ‖ CD; AD ‖ BC 3. A parallelogram is a quadrilateral with both pairs of opposite sides parallel. 4. ∠1 ≅ ∠2; ∠3 ≅ ∠4 4. If two parallel lines are cut by a transversal, the alternate interior angles are congruent 5. AC ≅ AC 5. Reflexive property: a quantity is congruent to itself. 6. ∆ABC ≅ ∆CDA 6. A-S-A: if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent. 7. AB ≅ CD; BC ≅ AD 7. CPCTC: corresponding parts of congruent triangles are congruent |
|
|
prove that opposite angles of a parallelogram are congruent using a two-column proof.
|
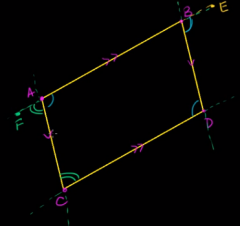
1. Parallelogram ABCD
1. Given 2. ∠CDB ≅ ∠EBD 2. Alternate interior angles are congruent 3. ∠EBD ≅ ∠BAC 3. Corresponding angles are congruent 4. ∠CDB ≅ ∠BAC 4. Substitution 5. ∠ACD ≅ ∠FAC 5. Alternate interior angles are congruent 6. ∠FAC ≅ ∠ABD 6. Corresponding angles are congruent 7. ∠ACD ≅ ∠ABD 7. Substitution |
|
|
prove that the diagonals of a parallelogram bisect each other.
|
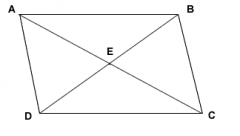
Given parallelogram ABCD with diagonals BD and AC which intersect at point E, ∠ABE is congruent to ∠CDE and ∠DEC is congruent to ∠BAE by the alternate interior angles theorem. Since we know that AB is congruent to DC, triangle ABE is congruent to triangle CDE by the angle-side-angle theorem of congruent triangles. Since the triangles are congruent, we can conclude that AE=CE and BE=DE because they are corresponding parts of congruent triangles. This proves that the diagonals bisect each other since E is the midpoint of each diagonal.
|
|
|
prove that rectangles are parallelograms with congruent diagonals.
|
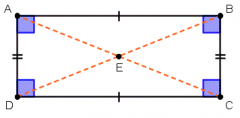
Given parallelogram ABCD with diagonals BD and AC, AB is congruent to DC and AD is congruent to BC because opposite sides of a parallelogram are congruent. Angle ABC is congruent to angle CDA because opposite angles of a parallelogram are congruent. This allows us to conclude that ∆ ABC is congruent to ∆ DCB by the side-angle-side theorem. Therefore, diagonal BD must be congruent to AC because they are corresponding parts of congruent triangles. We can also conclude that angle ABC and BCD are equal by CPCTC, meaning that all angles of the parallelogram must be equal, meaning that they must all be 90°, so the parallelogram must be a rectangle.
|

