Analysis

Front 1

cut

Back 1

a cut in Q is a pair of subsets A, B of Q such that

(1) AUB = Q, A, B not empty, intersection of A, B is not empty

(2) If a is in A and b is in B, then a < b

(3) A contains no largest element

Front 2

real number

Back 2

a cut in Q

Front 3

rational cut

Back 3

for some fixed rational number c, A is the set of all rationals < c while B is the rest of Q

Front 4

[x = A|B] < [y = C|D]

Back 4

x < y if A is contained in C

Front 5

upper bound

Back 5

M in R is an upper bound for a set S contained in R if each s in S satisfies S <= M

S is bounded above by M

Front 6

least upper bound

Back 6

an upper bound for a set that is less than all other upper bounds for the set

Front 7

T: the set R, constructed by means of Dedekind cuts, is complete in the sense that it satisfies the ____

Back 7

Least Upper Bound Property:

If S is a non-empty subset of R and is bounded above then in R there exists a least upper bound for S

Front 8

properties of cut addition

Back 8

well defined, natural, commutative, associative, has inverses with respect to 0

Front 9

properties of cut multiplication

Back 9

well defined, natural, commutative, associative, distributive over cut addition, has inverses of nonzero elements with respect to 1

Front 10

field

Back 10

a system consisting of a set of elements and two operations (addition and multiplication) that have the algebraic properties of cut addition and cut multiplication

Front 11

transitivity

Back 11

x < y < z implies x < z

Front 12

trichotomy

Back 12

either x < y, y < x, or x = y, but only one of the three things is true

Front 13

translation

Back 13

x < y implies x + z < y + z

Front 14

ordered fields have what properties?

Back 14

transitivity, trichotomy, and translation

Front 15

T: the set R of all cuts in Q is a ___

Back 15

complete ordered field that contains Q as an ordered subfield

Front 16

|x| for all x in R =

Back 16

x if x >= 0

-x if x <= 0

Front 17

triangle inequality

Back 17

for all x, y in R:

|x + y| <= |x| + |y|

Front 18

supremum

Back 18

the biggest number in a set

Front 19

infimum

Back 19

the lowest number in a set

Front 20

the sequence (an) converges to the limit b in R as n approaches infinity provided that ___

Back 20

for each e > 0, there exists m in N such that for all n >= m, |an - b| < e

Front 21

Cauchy condition

Back 21

for all e > 0, there exists p in N such that n, m >= p implies |an - am| < e

Front 22

every convergent sequence obeys ___

Back 22

a Cauchy condition

Front 23

R is complete with respect to Cauchy sequences in the sense that

Back 23

if (an) is a sequence of R#s obeying a Cauchy condition, then it converges to a limit in R

Front 24

a sequence (an) in R converges if and only if

Back 24

for all e > 0, there exists p in N such that n, m >= p implies |an - am| < e

Front 25

irrational numbers

Back 25

elements of R \ Q

Front 26

every interval (a, b) contains ___

Back 26

both rational and irrational numbers

Front 27

Archimedean property

Back 27

for each x in R there is an integer n that is greater than x; there exist arbitrarily large integers

Front 28

(e-principle) if a, b are R#s and if for each e > 0, a <= b + e, then ____; if x, y are R#s and for each e > 0, |x - y| <= e, then ____

Back 28

a <= b

x = y

Front 29

Cartesian product of sets A, B

Back 29

A x B, the set of all ordered pairs (a, b) such that a is in A and b is in B

Front 30

dot product

Back 30

= x1y1 + ... + xnyn

Front 31

length of a vector x in R^m

Back 31

|x| = sqrt() = sqrt(x1^2 + ... + xm^2)

Front 32

Cauchy-Schwarz Inequality

Back 32

for all x, y in R^m, <= |x||y|,y>

Front 33

triangle inequality for vectors

Back 33

for all x, y in R^m, |x + y| <= |x| + |y|

Front 34

Euclidean distance between vectors

Back 34

|x - y| = sqrt() = sqrt((x1 - y1)^2 + ... + (xm - ym)^2)

Front 35

integer lattice

Back 35

the set Z^m contained in R^m of ordered m-tuples of integers

Front 36

box

Back 36

a Cartesian product of intervals [a1, b1] x ... x [am, bm]

Front 37

unit cube in R^m

Back 37

the box [0, 1]^m

Front 38

unit ball in R^m

Back 38

{x in R^m: |x| <= 1}

Front 39

unit sphere in R^m

Back 39

{x in R^m: |x| = 1}

Front 40

convex

Back 40

a set E contained in R^m is convex if for each pair of points x, y in E, the straight line segment between x and y is also contained in E

Front 41

convex combinations

Back 41

linear combinations
sx + ty with s + t = 1 and 0 <= s, t <= 1

Front 42

inner product space

Back 42

a vector space equipped with an inner product

Front 43

norm

Back 43

any function || ||: V --> R with the three properties of vector length:

Front 44

three properties of vector length

Back 44

if v, w are in V and q in R, then

||v|| >= 0 and ||v|| = 0 if and only if v = 0

||qv|| = |q|||v||

||v + w || <= ||v|| + ||w||

Front 45

function

Back 45

a function f: A --> B is a rule or mechanism which, when presented with any element a in A, produces an element b = f(a) of B

Front 46

domain

Back 46

the set A of a function

Front 47

target

Back 47

the set B of a function

Front 48

range/image

Back 48

the subset of the target B:
{b in B: there exists at least one element a in A with f(a) = b}

Front 49

injection/one-to-one

Back 49

a mapping is an injection if for each pair of distinct elements a, a' in A, the elements f(a), f(a') are distinct in B

Front 50

surjection/onto

Back 50

a mapping is a surjection if for each b in B there is at least one a in A such that f(a) = b (i.e. the range of f is B)

Front 51

bijection

Back 51

a mapping which is both injective and surjective

Front 52

identity map

Back 52

the bijection that takes each a in A and sends it to itself

Front 53

composite

Back 53

f: A --> B, g: B --> C ====> g o f: A --> C

Front 54

properties of composites

Back 54

if f and g are injective, so is g o f; if f and g are surjective, so is g o f

Front 55

finite set

Back 55

empty or for some n in N, S ~ {1, ..., n}

Front 56

infinite set

Back 56

not finite

Front 57

denumerable set

Back 57

S ~ N

Front 58

countable set

Back 58

finite or denumerable

Front 59

uncountable set

Back 59

not countable

Front 60

R is (countable/uncountable)

Back 60

uncountable

Front 61

[a, b] and (a, b) are (countable/uncountable)

Back 61

uncountable

Front 62

each infinite set S contains ___

Back 62

a denumerable subset

Front 63

an infinite subset A of a denumerable set B is ___

Back 63

denumerable

Front 64

the sets of even integers and of prime integers are ___

Back 64

denumerable

Front 65

N x N is ___

Back 65

denumerable

Front 66

the Cartesian product of denumerable sets A and B is ___

Back 66

denumerable

Front 67

if f: N --> B is a surjection and B is infinite then B is ___

Back 67

denumerable

Front 68

the denumerable union of denumerable sets is ___

Back 68

denumerable

Front 69

Q is ___

Back 69

denumerable

Front 70

for each m in N, Q^m is ___

Back 70

denumerable

Front 71

every subset of a countable set is ___

Back 71

countable

Front 72

a countable set that contains a denumerable subset is ___

Back 72

denumerable

Front 73

the Cartesian product of finitely many countable sets is ___

Back 73

countable

Front 74

the countable union of countable sets is ___

Back 74

countable

Front 75

Schroeder-Bernstein Theorem

Back 75

if A, B are sets and f: A --> B, g: B --> A are injections, then there exists a bijection h: A --> B

Front 76

continuous

Back 76

a function f: [a, b] --> R is continuous if for each e > 0 and each x in [a, b], there is a d > 0 such that:
t in [a, b] and |t - x| < d implies |f(t) - f(x)| < e

Front 77

the values of a continuous function defined on an interval [a, b] ___; that is, there exist m, M in R such that ___

Back 77

form a bounded subset of R

for all x in [a, b], m <= f(x) <= M

Front 78

A continuous function f defined on an interval [a, b] takes on ____

Back 78

absolute minimum and absolute maximum values: for some x0, x1 in [a, b] and for all x in [a, b], f(x0) <= f(x) <= f(x1)

Front 79

Intermediate Value Theorem

Back 79

A continuous function defined on an interval [a, b] takes on all intermediate values: if f(a) = a', f(b) = b', and y is given, a' <= y <= b', then there is some c in [a, b] such that f(c) = y. The same conclusion holds if b' <= y <= a'

Front 80

Fundamental Theorem of Continuous Functions

Back 80

Every continuous real valued function of a real variable x in [a, b] is bounded, achieves minimum, intermediate, and maximum values, and is uniformly continuous

Front 81

uniformly continuous

Back 81

for each e > 0 there exists a d > 0 such that |x - t| < d implies that |f(x) - f(t)|< e

Front 82

metric properties

Back 82

positive definiteness

symmetry

triangle inequality

Front 83

positive definiteness

Back 83

d(x, y) >= 0, and d (x, y) = 0 iff x = y

Front 84

symmetry

Back 84

d(x, y) = d(y, x)

Front 85

triangle inequality

Back 85

d(x, z) <= d(x, y) + d(y, z)

Front 86

discrete metric

Back 86

the distance between distinct points is 1, between a point and itself is 0

Front 87

(pn) converges to the limit p in M if

Back 87

for all e > 0, there exists x in N such that:
n in N and n >= x implies d(pn, p) < e

Front 88

every subsequence of a convergent sequence ___

Back 88

converges and it converges to the same limit as does the mother sequence

Front 89

a function f: M --> N is continuous if ___

Back 89

it satisfies the delta epsilon condition

Front 90

delta epsilon condition

Back 90

for all e > 0 and for all p in M, there exists d > 0 such that q in M and d(p, q) < d implies d(fp, fq) < e

Front 91

f: M --> N is continuous iff ___

Back 91

it sends each convergent sequence in M to a convergent sequence in N, limits being sent to limits

Front 92

the composite of continuous functions is ___

Back 92

continuous

Front 93

homeomorphism

Back 93

if f: M --> N is a bijection and f is continuous and the inverse bijection f^-1: N --> M is also continuous and f is a homeomorphism

Front 94

limit

Back 94

a point p in M is a limit of S if there exists a sequence (pn) in S that converges to it

Front 95

closed set

Back 95

S is a closed set if it contains all its limits

Front 96

open set

Back 96

S is an open set if for each p in S there exists an r > 0 such that d(p, q) < r implies q in S

Front 97

relationship between openness and closedness

Back 97

the complement of an open set is closed and the complement of a closed set is open

Front 98

clopen

Back 98

subsets of M that are both closed and open

Front 99

topology of M

Back 99

the collection T of all open subsets of M

Front 100

properties of T

Back 100

(a) every union of open sets is an open set

(b) intersection of finitely many open sets is an open set

(c) empty set and M are open sets

Front 101

properties of closed sets

Back 101

(a) intersection of any number of closed sets is a closed set

(b) finite union of closed sets is a closed set

(c) empty set and M are closed sets

Front 102

limit set of S

Back 102

lim S = {p in M: p is a limit of S}

Front 103

r-neighborhood of p

Back 103

Mrp = {q in M: d(p, q) < r}

Front 104

lim S is (closed/open)

Back 104

closed

Front 105

Mrp is (closed/open)

Back 105

open

Front 106

What statement is equivalent to:

p is a limit of S

Back 106

for all r > 0, Mr(p) intersect S is not empty

Front 107

neighborhood

Back 107

a neighborhood of a point p in M is any open set V that contains p

Front 108

Every open set U in R can be uniquely expressed as ____

Back 108

a countable union of disjoint open intervals; the endpoints of the intervals do not belong to U

Front 109

pre-image

Back 109

fpre(V) = {p in M: f(p) in V}

Front 110

What are the equivalent conditions for continuity of f: M --> N?

Back 110

(a) epsilon-delta

(b) closed set condition

(c) open set condition

Front 111

closed set condition

Back 111

the pre-image of each closed set in N is closed in M

Front 112

open set condition

Back 112

the pre-image of each open set in N is open in M

Front 113

A homeomorphism f: M --> N bijects ____

Back 113

the collection of open sets in M to the collection of open sets in N

Front 114

closure

Back 114

cl(S) = intersection of K, where K ranges through the collection of all closed sets that contain S

cl(S) = {x in M: if K is closed and S in K, then x in K}

Front 115

interior

Back 115

int(S) = union of U where U ranges through the collection of all open sets contained in S

int(S) = {x in M: for some open U in S, x in U}

Front 116

boundary

Back 116

bd(S) = cl(S) intersection cl(S^c)

Front 117

cl(S) = ___

Back 117

lim S

Front 118

Inheritance Principle

Back 118

if K in N in M where M is a metric space and N is a metric subspace then K is closed in N iff there is some subset L of M such that L is closed in M and K = L intersect N; N inherits its closeds from M.

Front 119

a metric space inherits its ___ from the big space

Back 119

opens

Front 120

Assume that N is a metric subspace of M and also is a closed subset of M. A set K in N is closed in N iff ___

Back 120

it is closed in M

Front 121

Assume that N is a metric subspace of M and also is an open subset of M. A set U in N is open in N iff ___

Back 121

it is open in M

Front 122

The set S clusters at p if ___

Back 122

each Mrp contains infinitely many points of S

Front 123

The set S condenses at p if ___

Back 123

each Mrp contains uncountably many points of S

Front 124

What are equivalent conditions to S clustering at p?

Back 124

(1) there is a sequence of distinct points in S that converges to p

(2) each neighborhood of p contains infinitely many points of S

(3) each neighborhood of p contains at least two points of S

(4) each neighborhood of p contains at least one point of S other than p

Front 125

S union S' = ___

Back 125

cl(S)

Front 126

S is closed iff S' in ___

Back 126

S

Front 127

the least upper bound and the greatest lower bound of a non-empty bounded subset S in R belong to cl(S); thus, if S is closed, ___

Back 127

they belong to S

Front 128

Equivalencies for Convergence in a Product Space

Back 128

For a sequence pn = (p1n, p2n) in M = M1 x M2:

(1) (pn) converges with respect to metric dmax

(2) (pn) converges with respect to metric dE

(3) (pn) converges with respect to metric dsum

(4) (p1n) and (p2n) converge in M1 and M2 respectively

Front 129

A sequence in a Cartesian product of m metric spaces converges with respect to the sum metric iff ___

Back 129

it converges with respect to the max metric iff each component sequence converges

Front 130

Convergence in R^m

Back 130

A sequence of vectors (vn) in R^m converges in R^m iff each of its component sequences (vin) converges, 1 <= i <= m. The limit of the vector sequence is the vector v = lim (n-->inf) vn = (lim (n-->inf)v1n, ..., lim (n-->inf)vmn)

Front 131

the arithmetic operations of R are ___

Back 131

continuous

Front 132

the sums, differences, products, and quotients of real valued continuous functions are ___

Back 132

continuous

Front 133

Cauchy sequence

Back 133

the sequence (pn) in M that satisfies a Cauchy condition

for all e > 0, there exists x such that k, n >= N implies d(pk, pn) < e

Front 134

A metric space M is complete if ___

Back 134

each Cauchy sequence in M converges to a limit in M

Front 135

R^m is ___

Back 135

complete

Front 136

Every closed subset of a complete metric space is ___

Back 136

complete

Front 137

Every closed subset of Euclidean space is ___

Back 137

a complete metric space

Front 138

bounded

Back 138

A subset of a metric space M is bounded if for some p in M and some r > 0, S in MrP

Front 139

unbounded

Back 139

a set which is not bounded

Front 140

bounded function

Back 140

a function from M to another metric space N is a bounded function if its range is bounded; there exist q in N and r > 0 such that fM in Nrq

Front 141

sequentially compact

Back 141

a subset A of a metric space M is sequentially compact if every sequence (an) in A has a subsequence (ank) that converges to a limit in A

Front 142

every compact set is ___

Back 142

closed and bounded

Front 143

the closed interval [a, b] in R is ___

Back 143

compact

Front 144

the Cartesian product of two compact sets is ___

Back 144

compact

Front 145

the Cartesian product of m compact sets is ___

Back 145

compact

Front 146

Bolzano-Weierstrass Theorem

Back 146

any bounded sequence in R^m has a convergent subsequence

Front 147

a closed subset of a compact set is ___

Back 147

compact

Front 148

Heine-Borel Theorem

Back 148

every closed and bounded subset of R^m is compact

Front 149

if ... in An+1 in An in ... in A2 in A1, then (An) is a ___

Back 149

nested sequence of sets; intersection An = {p: for each n, p in An}

Front 150

the intersection of a nested sequence of compact non-empty sets is ___

Back 150

compact and non-empty

Front 151

diameter

Back 151

the diameter of a non-empty set S in M is the supremum of the distances d(x, y) between points of S

Front 152

If in addition to being nested, non-empty, and compact, the sets An have a diameter that tends to 0 as n-->inf, then A = intersect An is __

Back 152

a single point

Front 153

the continuous image of a compact is ___

Back 153

compact

Front 154

A continuous real valued function defined on a compact set is ___

Back 154

bounded; it assumes max and min values

Front 155

If M is compact and homeomorphic to N then N is ___

Back 155

compact

Front 156

If M is compact then a continuous bijection f: M --> N is ___

Back 156

a homeomorphism; its inverse bijection f^-1: N --> M is continuous

Front 157

a compact is ____

Back 157

absolutely closed and absolutely bounded

Front 158

every continuous function defined on a compact is ___

Back 158

uniformly continuous

Front 159

disconnected

Back 159

If M has a proper clopen subset A, M is disconnected

Front 160

connected

Back 160

M is connected if it contains no proper clopen subset

Front 161

the continuous image of a connected is ___

Back 161

connected

Front 162

If M is connected and M is homeomorphic to N, then N is ___

Back 162

connected

Front 163

Generalized Intermediate Value Theorem

Back 163

Every continuous real-valued function defined on a connected domain has the intermediate value property.

Front 164

R is ___

Back 164

connected

Front 165

Intermediate Value Theorem for R

Back 165

Every continuous function f: R --> R has the intermediate value property

Front 166

Some examples of connected metric spaces

Back 166

(a, b)

[a, b]

the circle

Front 167

the closure of a connected set is ___

Back 167

connected; more generally, if S in T in cl(S) and S is connected, then so is T

Front 168

the union of connected sets sharing a common point is ___

Back 168

onnected

c

Front 169

path

Back 169

a path joining p to q in a metric space M is a continuous function f: [a, b] --> M such that fa = p and fb = q

Front 170

path-connected

Back 170

if each pair of points in M can be joined by a path in M, then M is path-connected

Front 171

path-connected implies

Back 171

connected

Front 172

all connected subsets of R are ___

Back 172

path connected

Front 173

covering

Back 173

a collection U of subsets of M covers A in M if A is contained in the union of the sets belonging to U; U is a covering of A

Front 174

subcovering

Back 174

if U and V both cover A and V in U, then U reduces to V and V is a subcovering

Front 175

open covering

Back 175

if all sets in U are open, U is an open covering of A

Front 176

covering compact

Back 176

if every open covering of A reduces to a finite subcovering then we say that A is covering compact

Front 177

are covering compact and sequentially compact equivalent?

Back 177

yes

Front 178

Lebesgue number

Back 178

a Lebesgue number for a covering U of A is a positive real number w such that for each a in A there is some K in U with Mwa in K

Front 179

Lebesgue Number Lemma

Back 179

every open covering of a sequentially compact set has a Lebesgue number w > 0

Front 180

totally bounded

Back 180

a set A in M is totally bounded if for each e > 0 there exists a finite covering of A by e-neighborhoods

Front 181

Generalized Heine-Borel Theorem

Back 181

A subset of a complete metric space is compact iff it is closed and totally bounded

Front 182

a metric space is compact iff ___

Back 182

it is complete and totally bounded

Front 183

perfect

Back 183

a metric space M is perfect if M' = M: each p in M is a cluster point of M

Front 184

every non-empty, perfect, complete metric space is __

Back 184

uncountable

Front 185

R and [a, b] are both ___

Back 185

uncountable

Front 186

A non-empty perfect complete metric space is ___

Back 186

everywhere uncountable in the sense that each r-neighborhood is uncountable

Front 187

the function f: (a, b) --> R is differentiable at x if

Back 187

lim(t-->x) [f(t) - f(x)] / [t - x] = L

Front 188

derivative

Back 188

f'(x) = lim(t-->x) [f(t) - f(x)] / [t - x] = L

Front 189

differentiability at x means ___

Back 189

f'(x) = lim (change in x --> 0) [change in f] / [change in x]

Front 190

differentiability implies ___

Back 190

continuity

Front 191

f, g differentiable at x implies (+)

Back 191

f + g is differentiable at x:

(f + g)'(x) = f'(x) + g'(x)

Front 192

f, g differentiable at x implies (*)

Back 192

f * g is differentiable at x:

(f * g)'(x) = f'(x) * g(x) + f(x) * g'(x)

Front 193

the derivative of a constant is

Back 193

0; c' = 0

Front 194

f, g differentiable at x and g(x) not equal to 0 implies

Back 194

f/g is differentiable at x:

(f/g)'(x) = (f'(x) * g(x) - f(x) *g'(x)) / [g(x)]^2

Front 195

if f is differentiable at x and g is differentiable at y = f(x) then ___

Back 195

g o f is differentiable at x:

(g o f)'(x) = g'(y) * f'(x)

Front 196

the derivative of a polynomial ___

Back 196

exists everywhere

Front 197

differentiable

Back 197

a function f: (a, b) --> R that is differentiable at each x in (a, b) is differentiable

Front 198

Mean Value Theorem

Back 198

a continuous function f: [a, b] --> R that is differentiable on the interval (a, b) has the mean value property

Front 199

mean value property

Back 199

there exists a point d in (a, b) such that:

f(b) - f(a) = f'(d)(b - a)

Front 200

If f is differentiable and |f'(x)| <= M for all x in (a, b) then ___

Back 200

f satisfies the global Lipschitz condition

Front 201

global Lipschitz condition

Back 201

for all t, x in (a, b):

|f(t) - f(x)| <= M|t - x|

Front 202

if f'(x) = 0 for all x in (a, b), then ___

Back 202

f(x) is constant

Front 203

Ratio Mean Value Theorem

Back 203

suppose that the functions f and g are continuous on [a, b] and differentiable on (a, b); then there is a k in (a, b) such that dfg'(k) = dgf'(k), where df = f(b) - f(a) and dg = g(b) - g(a)

Front 204

L'Hopital's Rule

Back 204

if f, g are differentiable functions defined on (a, b), both of which tend to 0 at b, and if the ratio of their derivatives f'(x)/g'(x) tends to a finite limit L at b then f(x)/g(x) also tends to L at b (we assume g(x), g'(x) do not equal 0)

Front 205

if f is differentiable on (a, b) then its derivative function f'(x) ___

Back 205

has the intermediate value property

Front 206

the derivative of a differentiable function ___

Back 206

never has a jump discontinuity

Front 207

if f^r(x) exists, then f is ___

Back 207

rth order differentiable at x

Front 208

if f^r(x) exists for all x in (a, b), then f is ___

Back 208

rth order differentiable

Front 209

if f^r(x) exists for all r and all x then f is ___

Back 209

infinitely differentiable/smooth

Front 210

the zeroth derivative of f is __

Back 210

f itself

Front 211

a smooth function is ___; each derivative of a smooth function is ___

Back 211

continuous

smooth and thus continuous

Front 212

if f is differentiable and its derivative function f'(x) is a continuous function of x, then f is ___

Back 212

continuously differentiable (f is of class C^1)

Front 213

if f is rth order differentiable and f^r(x) is a continuous function of x, then f is ___

Back 213

continuously rth order differentiable (f is of class C^r)

Front 214

if f is smooth, it is of class __

Back 214

C^inf

Front 215

a continuous function is of class ___

Back 215

C^0

Front 216

analytic function

Back 216

a function which can be expressed locally as a convergent power series:

the function f: (a, b) --> R is analytic if for each x in (a, b), there exists a power series sum(a,r,h^r) and a d > 0 such that if |h| < d then the series converges and f(x + h) = sum[0-->inf](a,r,h^r)

Front 217

rth order Taylor polynomial of an rth order differentiable function f at x

Back 217

Front 218

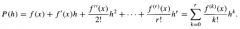
Taylor Approximation Theorem

Back 218

Assume that f: (a, b) --> R is rth order differentiable at x. Then:
(1) P approximates f to order r at x in the sense that the Taylor remainder R(h) = f(x + h) - P(h) is rth order flat at h = 0; R(h)/h^r --> 0 as h --> 0

(2) The Taylor polynomial is the only polynomial of degree <= r with this approximation property

(3) If, in addition, f is (r + 1)st order differentiable on (a, b) then for some d between x and x + h, R(h) = [f^(r+1)(d) / (r+1)!]*h^(r+1)

Front 219

for each r in N, the smooth non-analytic function e(x) satisfies ___

Back 219

lim[h-->0] e(h) / h^r = 0

Front 220

Taylor series at x of a smooth function f

Back 220

T(h) = sum[0-->inf]((f^r(x) / r!)*h^r)

Front 221

Inverse Function Theorem in dimension one

Back 221

if f: (a, b) --> (c, d) is a differentiable surjection and f'(x) is never zero then f is a homeomorphism, and it inverse is differentiable with derivative (f^-1)'(y) = 1/f'(x) where y = f(x)

Front 222

if a homeomorphism f and its inverse are both of class C^r, r >= 1, then f is a ___

Back 222

C^r diffeomorphism

Front 223

if f: (a, b) --> (c, d) is a homeomorphism of class C^r, 1 <= r <= inf, and f' not equal to 0, then f ___

Back 223

is a C^r diffeomorphism

Front 224

undergraph of f

Back 224

"U" = {(x, y): a <= x <= b and 0 <= y <= f(x)}

Front 225

partition pair

Back 225

consists of two finite sets of points, P, T in [a, b];
P = {x0, ..., xn} and T = {t1, ..., tn}, interlaced as

a = x0 <= t1 <= x1 <= t2 <= ... <= tn <= xn = b

Front 226

Riemann sum corresponding to f, P, T

Back 226

R(f, P, T) = sum[1-->n](f(ti)dx(i)) (dx = change in x)

Front 227

mesh of the partition P

Back 227

the length of the largest subinterval [xi-1, xi]

Front 228

coarse

Back 228

a partition with large mesh

Front 229

fine

Back 229

a partition with small mesh

Front 230

Riemann integral

Back 230

a real number I is a the Riemann integral of f over [a, b] if it satisfies the approximation condition:

for all e > 0 there exists d > 0 such that if P, T is any partition pair then mesh P < d implies |R - I| < e

where R = R(f, P, T)

Front 231

int[a, b](f(x)dx) = ___

Back 231

I = lim[mesh P-->0](R(f, P, T))

Front 232

If f is Riemann integrable then it is ___

Back 232

bounded

Front 233

Linearity of the Integral

Back 233

(a) "R" is a vector space and f --> int[a, b](f(x)dx) is a linear map "R" --> R

(b) The constant function h(x) = k is integrable and its integral is k(b - a)

Front 234

Monotonicity of the Integral

Back 234

if f, g in "R" and f <= g then
int[a,b](f(x)dx) <= int[a,b](g(x)dx)

Front 235

If f in "R" and |f| <= M then ___

Back 235

|int[a,b](f(x)dx)| <= M(b - a)

Front 236

lower sum of f: [a, b] --> [-M, M] with respect to partition P

Back 236

L(f, P) = sum[1,n](mi*dxi) (dx = change in x)

mi = inf{f(t): xi-1 <= t <= xi}

Front 237

upper sum of f: [a, b] --> [-M, M] with respect to partition P

Back 237

U(f, P) = sum[1,n](Mi*dxi) (dx = change in x)

Mi = sup{f(t): xi-1 <= t <= xi}

Front 238

lower integral of f over [a,b]

Back 238

low(I) = sup L(f, P)

Front 239

upper integral of f over [a,b]

Back 239

upp(I) = inf U(f, P)

Front 240

Darboux integrable

Back 240

if low(I) = upp(I) then f is Darboux integrable and their common value is f's Darboux integral

Front 241

Riemann integrability is equivalent to

Back 241

Darboux integrability; when a function is integrable, its three integrals (lower, upper, and Riemann) are equal

Front 242

The partition P' refines P if

Back 242

P' contains P

Front 243

Refinement Principle

Back 243

Refining a partition causes the lower sum to increase and the upper sum to decrease

Front 244

common refinement

Back 244

the common refinement P* of two partitions P, P' of [a, b] is P* = P union P'

Front 245

A bounded function f: [a,b] --> R is Darboux integrable iff

Back 245

for all e > 0 there exists P such that U(f, P) - L(f, P) < e

Front 246

Riemann's Integrability Criterion

Back 246

A bounded function is Riemann integrable iff for all e > 0 there exists P such that U(f,P) - L(f,P) < e

Front 247

zero set

Back 247

a set Z in R is a zero set if for each e > 0 there is a countable covering of Z by open intervals (ai,bi) such that sum[1,inf](bi - ai) <= e

Front 248

if a property holds for all points except those in a zero set, then the property holds __

Back 248

almost everywhere (a.e.)

Front 249

Riemann-Lebesgue Theorem

Back 249

a function f: [a,b] --> R is Riemann integrable iff it is bounded and its set of discontinuity points is a zero set

Front 250

Every continuous function is ____

Back 250

Riemann integrable, and so is every bounded piecewise continuous function

Front 251

The characteristic function of S in [a, b] is Riemann integrable iff

Back 251

the boundary of S is a zero set

Front 252

Every monotone function is ___

Back 252

Riemann integrable

Front 253

The product of Riemann integrable functions is ___

Back 253

Riemann integrable

Front 254

If f:[a,b] --> [c,d] is Riemann integrable and g:[c,d] --> R is continuous, then the composite function g o f is ___

Back 254

Riemann integrable

Front 255

if f in "R" then |f| in ___

Back 255

R

Front 256

if a < c < b and f: [a,b] --> R is Riemann integrable then ___

Back 256

its restrictions to [a,c], [c,b] are Riemann integrable and:
int[a,b](f(x)dx) = int[a,c](f(x)dx) + int[c,b](f(x)dx)

Front 257

Riemann integrability on [a,c] and [c,b] implies

Back 257

Riemann integrability on [a,b]

Front 258

If f: [a,b] --> [0, M] is Riemann integrable and has integral zero then ___

Back 258

f(x) = 0 at every continuity point x of f; that is, f(x) = 0 a.e.

Front 259

If f is Riemann integrable and g is a bijection whose inverse satisfies a Lipschitz condition then f o g is ___

Back 259

Riemann integrable

Front 260

If f in "R" and g: [c, d] --> [a, b] is a C^1 diffeomorphism then f o g is ___

Back 260

Riemann integrable

Front 261

Fundamental Theorem of Calculus

Back 261

If f: [a,b] --> R is Riemann integrable then its indefinite integral F(x) = int[a,x](f(t)dt) is a continuous function of x. The derivative of F(x) exists and equals f(x) at all points x at which f is continuous.

Front 262

The derivative of an indefinite Riemann integral __

Back 262

exists almost everywhere and equals the integrand almost everywhere

Front 263

if one function is the derivative of the another, the second function is an ___ of the first

Back 263

antiderivative

Front 264

every continuous function has an

Back 264

antiderivative

Front 265

Antiderivative Theorem

Back 265

An antiderivative of a Riemann integrable function, if it exists, differs from the indefinite integral by a constant

Front 266

Standard integral formulas are

Back 266

valid

Front 267

logarithm function

Back 267

log x = int[1,x]((1/t)dt)

Front 268

There exists a continuous function H:[0,1] --> R whose derivative exists and equals zero almost everywhere, but which is ___

Back 268

not constant

Front 269

Integration by Substitution

Back 269

If f in "R" and g: [c,d] --> [a,b] is a continuously differentiable bijection with g' > 0 (g is a C^1 diffeomorphism) then:

int[a,b](f(y)dy) = int[c,d](f(g(x))g'(x)dx)

Front 270

Integration by Parts

Back 270

if f, g:[a,b] --> R are differentiable and f', g' in "R" then:

int[a,b](f(x)g'(x)dx) = f(b)g(b) - f(a)f(b) - int[a,b](f'(x)g(x)dx)

Front 271

Improper Riemann integral

Back 271

int[a,b](f(x)dx) = lim[c-->b](int[a,c](f(x)dx))

Front 272

convergence of a series

Back 272

a series converges to A if An --> a as n --> inf

A = sum[0,inf](a,k,)

Front 273

divergence

Back 273

a series that does not converge

Front 274

CCC for series

Back 274

sum(a,k,) converges iff for all e > 0 there exists N such that m, n >= N implies |sum[m,n](a,k,)| < e

Front 275

comparison test

Back 275

if a series sum(b,k,) dominates a series sum(a,k,) in the sense that for all sufficiently large k, |a,k,|| <= b,k, then convergence of sum(b,k,) implies convergence of sum(a,k,)

Front 276

absolute convergence

Back 276

series sum(a,k,) converges absolutely if sum(|a,k,|) converges

Front 277

Integral Test

Back 277

Suppose that int[0,inf](f(x)dx) is a given improper integral and sum(a,k,) is a given series:

(a) if |a,k,| <= f(x) for all sufficiently large k and all x in (k - 1, k] then convergence of the improper integral implies convergence of the series.

(b) if |f(x)| <= a,k, for all sufficiently large k and all x in [k, k + 1) then divergence of the improper integral implies divergence of the series

Front 278

exponential growth rate of the series sum(a,k,)

Back 278

ex = lim[k-->inf](sup(krt(|a,k,|)))

Front 279

Root Test

Back 279

Let ex be the exponential growth rate of a series sum(a,k,); if ex < 1 the series converges, if ex > 1 the series diverges, and if ex = 1 the test is inconclusive

Front 280

Ratio Test

Back 280

let the ratio between successive terms of the series sum(a,k,) be r,k, = |a,k+1, / a,k,| and set lim[k-->inf](inf(r,k,)) = q, lim[k-->inf](sup(r,k,)) = w. If w < 1 the series converges; if q > 1 the series diverges; otherwise the test is inconclusive

Front 281

alternating series

Back 281

if (a,k,) is a decreasing sequence in R that converges to 0 then its alternating series sum((-1)^(k+1)a,k,) = a1 - a2 + a3 - ... converges

Front 282

series of functions

Back 282

sum[0,inf](f,k,(x)); each term f,k,:(a, b) --> R is a function

Front 283

Radius of Convergence Theorem

Back 283

if sum(c,k,x^k) is a power series then there is a unique r, 0 <= r 0 <= inf, its radius of convergence, such that the series converges whenever |x| < r, and diverges whenever |x| > r

R = 1 / (lim[k-->inf](sup(krt(|c,k,|))))

Front 284

pointwise convergence

Back 284

a sequence of functions fn: [a,b] --> R converges pointwise to a limit function f:[a,b] --> R if for each x in [a,b] lim[n-->inf](fn(x)) = f(x)

Front 285

uniform convergence

Back 285

the sequence of functions fn:[a,b] --> R converges uniformly to the limit function f:[a,b] --> R if for each e > 0 there is an N such that for all n >= N and all x in [a,b], |fn(x) - f(x| < e

Front 286

If fn ==>> f and each fn is continuous at x0 then f is ___

Back 286

continuous at x0; the uniform limit of continuous functions is continuous

Front 287

C,b, is

Back 287

the set of all bounded functions [a,b] --> R

Front 288

||f|| = ___ (sup norm)

Back 288

sup{|f(x)|: x in [a,b]}

Front 289

sup norm satisfies:

Back 289

||f|| >= 0 and ||f|| = 0 iff f = 0

||cf|| = |c|||f||

||f + g|| <= ||f|| + ||g||

Front 290

Convergence with respect to the sup-metric d is ___

Back 290

equivalent to uniform convergence

Front 291

d(f, g) = ___

Back 291

sup{|f(x) - g(x)|: x in [a,b]}

Front 292

Cb is a ___

Back 292

complete metric space

Front 293

C^0 is a ___

Back 293

closed subset of Cb; it is a closed metric space

Front 294

Weierstrass M-test

Back 294

if sum(M,k,) is a convergent series of constants and if f,k, in C,b, satisfies ||f,k,|| <= M,k, for all k, then sum(f,k,) converges uniformly and absolutely

Front 295

The uniform limit of Riemann integrable functions is ___

Back 295

Riemann integrable, and the limit of the integrals is the integral of the limit:

lim[n-->inf](int[a,b](fn(x)dx)) = int[a,b](unif lim[n-->inf](fn(x)dx))

Front 296

If fn in "R" and fn ==>> f then ___

Back 296

the indefinite integrals converge uniformly:
int[a,x](fn(t)dt) ==>> int[a,x](f(t)dt)

Front 297

Term by Term Integration Theorem

Back 297

A uniformly convergent series of integrable functions sum(f,k,) can be integrated term by term in the sense that:
int[a,b](sum[0,inf](fk(x)dx)) = sum[0,inf](int[a,b](fk(x)dx))

Front 298

The uniform limit of a sequence of differentiable function is differentiable provided that ___

Back 298

the sequence of derivatives also converges uniformly

Front 299

Term by Term Differentiation Theorem

Back 299

A uniformly convergent series of differentiable functions can be differentiated term by term, provided that the derivative series converges uniformly:
(sum[0,inf](fk(x)))' = sum[0,inf](f,k,'(x))