![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
50 Cards in this Set
- Front
- Back
|
Restklasse |
Sei u ∈ ℕ \ {0} beliebig. Für die Äquivalenzklassen der Relation |
|
|
Die Menge aller Restklassen mod u (ℤᵤ) bilden einen Körper, wenn ... |
... u eine Primzahl ist. |
|
|
−4 mod 5 = |
1 |
|
|
3 + x ≡ 2 (mod 5)
auflösen nach x |
Zu beiden Seiten −3 addieren, damit links x übrigbleibt. |
|
|
a ≡ b (mod q) ↔
|
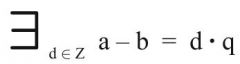
Wenn a und b kongruent sind modulo q, dann ist ihre Differenz ein ganzzahliges Vielfaches von q. |
|
|
Rechnen mit Restklassen |
Man will in ℤᵤ rechnen (d.h. mit den Restklassen [x]ᵤ). |
|
|
232 · 348 ≡ ? (mod 5) |
≡ 2 · 3 ≡ 6 ≡ 1 (mod 5) |
|
|
3^172 ≡ ? (mod 7) |
Wenn Exponent unhandlich, muss er in 2er-Potenzen zerlegt werden: |
|
|
7^6 ≡ ? (mod 5) |
Die Basis darf durch die Restklasse repräsentiert werden. D.h. statt 7 darf man 2 (mod 5) verwenden: |
|
|
Addition von Restklassen
|
[a]ᵤ + [b]ᵤ = [a + b]ᵤ |
|
|
Multiplikation von Restklassen |
[a]ᵤ · [b]ᵤ = [a · b]ᵤ |
|
|
Wann ist diese lineare diophantische Gleichung lösbar (a,b,c ∈ ℤ)? |
Genau dann lösbar, wenn ggT(a,b) | c |
|
|
Solving a linear Diophantine equation (in two variables x and y). |
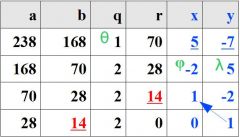
238x + 168y = 126 |
|
|
ALLE Lösungen einer diophantischen Gleichung ableiten, wenn man eine Lösung (x₀, y₀) gefunden hat. |
Für beliebge i ∈ ℤ: |
|
|
Wie löst man das? |
Es wird als diophantische Gleichung geschrieben mit Pluszeichen: |
|
|
Inverses Element der Multiplikation für eine Restklasse bestimmen. (allgemein) |
Gesucht: Das inverse Element 3⁻¹ zu 3 in ℤ₇. |
|
|
Inverses Element der Multiplikation für eine Restklasse bestimmen. (einfacher Fall) |
Gesucht: Das inverse Element 9⁻¹ zu 9 in ℤ₁₀.
9 ≡ −1 mod 10
Variante A: Man überlegt sich ganz einfach, was das multiplikative Inverse zu −1 ist: Womit muss man −1 multiplizieren, damit das neutrale Element 1 rauskommt?
Variante B: Man darf stur ausrechnen:
Das multiplikative Inverse 9⁻¹ zu [9]₁₀ ist also −1 bzw. die [9]₁₀ selbst: 9⁻¹ ≡ −1 ≡ 9 mod 10
Merke: |
|
|
Division von Restklassen |
Multiplikation mit dem Inversen der Multiplikation des Divisors. Nur definiert wenn ℤᵤ ein Körper ist, d.h. u ist prim. |
|
|
Bestimme x: |
Man bestimmt das multiplikative Inverse für 20 (nämlich [8]₅₃) und multipliziert die Gleichung damit: |
|
|
ac ≡ bc mod m |
Nur wenn c und m teilerfremd sind, d.h. ggT(c, m) = 1. |
|
|
Diese spezielle diophantische Gleichung hat 1 auf der rechten Seite. |
Nur lösbar wenn a und u teilerfremd sind. |
|
|
Was kann man über die Resultate r und u sagen? |
Die Resultate r und u sind teilerfremd. |
|
|
Chinesischer Restsatz |
x ≡ a mod m |
|
|
Wie findet man x mit: |
Chinesischer Restsatz. Oder alternativ so: |
|
|
Sei u eine beliebige Primzahl. |
Die Gleichung ist stets eindeutig lösbar. |
|
|
Prüfziffer für 10-stellige ISBN-Nummer |
9 Ziffern plus 1 Prüfziffer. |
|
|
Prüfziffer für 13-stellige ISBN-Nummer |
12 Ziffern plus 1 Prüfziffer. |
|
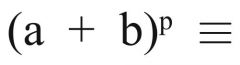
Sei p ∈ ℕ eine Primzahl, a, b ∈ ℤ beliebig, |
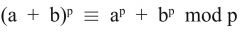
|
|
|
Eulersche Phi–Funktion |
φ(n) = |{a ∈ ℕ | 1 <= a <= n ^ ggT(a,n) =1 }| |
|
|
Eulersche Phi–Funktion einer Primzahl p? |
φ(p) = p − 1 |
|
|
φ(m · n) = ? |
φ(m · n) = φ(m) · φ(n) |
|
|
Wie wird die Eulersche Phi–Funktion für die n-te Potenz einer Primzahl p berechnet? |
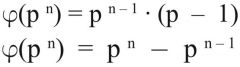
|
|
|
Eulersche Phi–Funktion für eine beliebige Zahl?
φ(n) |
φ(n) am Beispiel φ(12) |
|
|
Satz von Euler |
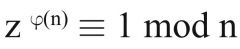
ggT(z, n) = 1 |
|
|
Summatorische Funktion der Eulerschen Phi-Funktion |
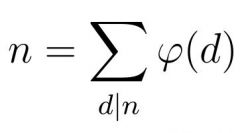
Wenn man alle Teiler d einer Zahl n nimmt, für jedes d φ(d) bestimmt und diese alle summiert, dann gibt das n. |
|
|
Fermat’s Little Theorem |
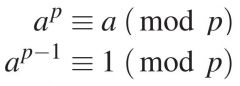
Let a be an integer and p be a prime. |
|
|
Anwendung von Fermats kleinem Satz, um das multiplikative Inverse a⁻¹ zu einer Zahl a bezüglich Restklasse p (prim) zu berechnen. |
![Die Gleichung aus Fermats kleinem Satz wird umgewandelt, indem man zuerst ein a aus der Potenz herausholt (obere Gleichung) und dann mit dem Inversen zu a (a−¹) multipliziert (untere Gleichung).
Inverses zu [2]₅ ≡ 2^(5 − 2) ≡ 2^3 ≡...](https://images.cram.com/images/upload-flashcards/03/54/02/5035402_m.jpg)
Die Gleichung aus Fermats kleinem Satz wird umgewandelt, indem man zuerst ein a aus der Potenz herausholt (obere Gleichung) und dann mit dem Inversen zu a (a⁻¹) multipliziert (untere Gleichung). |
|
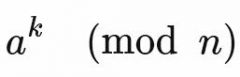
Vereinfache! |
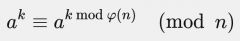
Wenn ggT(a,n) = 1, dann gilt die Gleichung auf dem Bild für alle k ≥ 1.
Bsp:
φ(5) = 4 (5 ist prim) Somit:
Oder in diesem Fall kann die Basis a auch trivial im Modul 5 ausgedrückt werden: 4 ≡ −1 (mod 5) Und damit: 4^1007 ≡ (−1)^1007 ≡ −1 ≡ 4 mod 5 |
|
|
The Fermat test for primality |
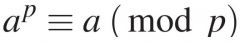
In Fermat's little theorem, if p is not prime, then, in general, most of the numbers a < p will not satisfy the above relation. |
|
|
Aus φ(x) wieder x zurückgewinnen? |
Das φ(x) in Faktoren zerlegen und solche Ausdrücke mit Primzahlen p anstreben: |
|
|
Der grosse Satz von Fermat |
a^n + b^n = c^n |
|
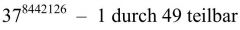
Wie prüft man, ob diese Aussage wahr ist? |
1) Das Modul 49 ist keine Primzahl (also kleiner Fermat nicht anwendbar) |
|
|
x = 5^254 mod 196
|
1) Das Modul 196 ist keine Primzahl (also kleiner Fermat nicht anwendbar) |
|
|
Der RSA ist ... |
... ein asymmetrisches Verschlüsselungsverfahren, von Ron Rivest, Adi Shamir und Leonard Adleman. |
|
|
RSA Key Generierung |
1) Wähle zufällig (!) zwei grosse Primzahlen p und q (100 und mehr Stellen) |
|
|
RSA Verschlüsselung und Entschlüsselung
|
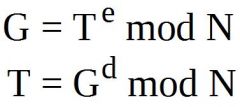
T = Klartext |
|
|
Beweis, dass RSA Verschlüsselung + Entschlüsselung wieder den Klartext ergibt. |
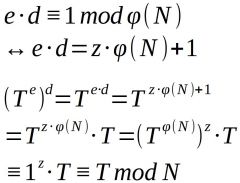
z = beliebige, positive, ganze Zahl |
|
|
Digitale Signatur
|
Arbeitet mit RSA Verschlüsselung. |
|
|
RSA Message Grösse |
Since a message m is only unique up to the size of the modulus N, we cannot encrypt more than b bits with one RSA encryption, where b is the bit length of N. |
|
|
43^7 mod 55 ohne Taschenrechner? |
43^7
Es gilt:
Und weiter:
Einsetzen: |

