Snl Algebraische Strukturen

Front 1

Wozu algebraische Strukturen?

Back 1

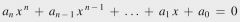
Reelle Zahlen kann man addieren und multiplizieren. Derartige Operationen lassen sich jedoch auch für viele andere mathematische Objekte erklären. Das führt auf die Begriffe Gruppe, Ring und Körper, die sich im Zusammenhang mit der Lösung algebraischer Gleichungen und der Lösung zahlentheoretischer und geometrischer Probleme im 19. Jahrhundert herauskristallisiert haben.

Man muss ein Problem auf einer möglichst hohen Abstraktionsebene einmal lösen, sodass man diese Lösung auf alle möglichen konkreten Fälle anwenden kann.

Indem Betrachtungen so verallgemeinert werden, dass nicht mehr von konkreten Zahlen die Rede ist, zeigt man: In allen Mengen, die die analysierten Eigenschaften haben, sind gewisse Gleichungen stets eindeutig lösbar. Diese Mengen können dann auch aus z. B. Matrizen oder Abbildungen bestehen.

Algebraische Strukturen ermöglichen also Aussagen zur Lösbarkeit algebraischer Gleichungen n-ten Grades, mit einer Unbekannten t.

Front 2

abgeschlossene Verknüpfung

Back 2

Eine Verknüpfung ♦ in einer Menge M ist eine Vorschrift, die je zwei Elementen a und b der Menge M ein drittes Element c zuordnet.
Die Menge M heisst abgeschlossen bezüglich ♦, wenn jedes c = a ♦ b wieder zu M gehört.

Beispiel:
Menge G = { 2ⁿ | n ∈ ℤ }
Die Addition (G, + ) ist z.B. nicht abgeschlossen, denn 2^3 + 2^4 = 8 + 16 = 24, also nicht mehr eine Zweierpotenz.
Die Multiplikation (G, · ) dagegen ist abgeschlossen.

Front 3

Gruppe

(algebraische Struktur)

Back 3

#3

Das Tupel (G, ♦), bestehend aus einer Menge G mit einer Verknüpfung ♦ heisst Gruppe, wenn gilt:

1) ABGESCHLOSSEN:
x, y ∈ G → x ♦ y ∈ G für alle x, y ∈ G

2) ASSOZIATIVGESETZ:
x ♦ (y ♦ z) = (x ♦ y) ♦ z

3) Es gibt das NEUTRALE ELEMENT n zur Verknüpfung ♦, so dass für jedes x gilt:
x ♦ n = n ♦ x = x
(das gleiche n für alle x)

4) Für jedes x kann ein INVERSES ELEMENT i gefunden werden, so dass gilt:
x ♦ i = i ♦ x = n
(das können individuelle i sein für verschiedene x, es resultiert immer das gleiche neutrale Element n)

{engl. group}

Front 4

Kommutative Gruppe

(algebraische Struktur)

Back 4

Wenn für eine Gruppe zusätzlich das Kommutativgesetz gilt, dann spricht man von einer kommutativen Gruppe (auch abelsche Gruppe):

KOMMUTATIVGESETZ:
x ♦ y = y ♦ x

Front 5

Ring
(algebraische Struktur)

Back 5

#2

Eine Menge R mit den Verknüpfungen + und · heißt ein Ring, wenn für (R, +, ·) gilt:

0) ABGESCHLOSSEN bezüglich beider Operationen + und ·. Das folgt bereits aus der Definition der Operationen an sich und wird normalerweise nicht extra erwähnt. Siehe ganz unten.

1) KOMMUTATIVE GRUPPE bezüglich der ADDITION.

2) ASSOZIATIVGESETZ bezüglich der MULTIPLIKATION:
x · (y · z) = (x · y) · z

3) DISTRIBUTIVGESETZ:
x · (y + z) = x · y + x · z
(y + z) · x = y · x + z · x

{engl. ring}

"Addition and multiplication are both, by definition, binary operations on R, i.e., functions from R × R → R. Closure is built into the definition of a binary operation: x + y and x · y are, by definition, elements of R."

Front 6

Kommutativer Ring
(algebraische Struktur)

Back 6

Falls bei einem Ring zusätzlich das Kommutativgesetz bezüglich der Multiplikation erfüllt ist, heißt (R, +, ·) ein kommutativer Ring.

KOMMUTATIVGESETZ:
x · y = y · x

Front 7

Körper
(algebraische Struktur)

Back 7

#1

Eine Menge K mit den Verknüpfungen + und · heißt ein Körper, wenn für (K, +, ·) gilt:

1) KOMMUTATIVE GRUPPE bezüglich der ADDITION.

2) GRUPPE bezüglich der MULTIPLIKATION ohne 0. D.h. (K \ {0}, ·) ist eine Gruppe.
("ohne 0" weil inverse Elemente nur für x ≠ 0 verlangt sind)

3) DISTRIBUTIVGESETZ:
x · (y + z) = x · y + x · z
(y + z) · x = y · x + z · x

{engl. field}

Front 8

Kommutativer Körper
(algebraische Struktur)

Back 8

Falls (K \ {0}, ·) nicht nur eine Gruppe, sondern eine kommutative Gruppe ist, heißt (K, +, ·) ein kommutativer Körper.
Es gilt also zusätzlich das KOMMUTATIVGESETZ bezüglich der MULTIPLIKATION:

KOMMUTATIVGESETZ:
x · y = y · x

Front 9

Unterschied zwischen Ring und Körper?

Back 9

Die Unterschiede betreffen die MULTIPLIKATION. Im Körper gibt es zusätzlich:

1) Das NEUTRALE ELEMENT der Multiplikation.
2) INVERSE ELEMENTE der Multiplikation für jedes x.

(Zudem kann sowohl bei Ring als auch Körper optional das Kommutativgesetz für die Multiplikation gelten. Das bringt aber keine Differenzierung, da bei beiden algebraischen Strukturen möglich.)

Front 10

Was nützt eine Gruppe hinsichtlich dem Lösen von Gleichungen?

Back 10

(G, ♦) sei eine Gruppe, a und b beliebige Elemente aus G. Das inverse Element zu a sei i.
Dann hat die Gleichung
a ♦ x = b
genau eine Lösung in G, nämlich:
x = i ♦ b

Front 11

Was nützt ein Körper hinsichtlich dem Lösen von Gleichungen?

Back 11

Sei K ein beliebiger Körper. Seien a und b ∈ K beliebig, a ≠ 0 mit multiplikativem Inversen i, b mit additivem Inversen (−b).
Dann ist die Gleichung
a · x + b = 0
in K eindeutig lösbar, nämlich:
x = i · (−b)

Front 12

Ist das Tupel (ℕ, +) eine Gruppe?

Back 12

Nein, ist gar nichts. Es reicht nicht einmal zur Gruppe!
Denn ℕ hat kein inverses Element für die Addition (nur die 0 hat eins).

Front 13

Welche Matrizen bilden einen Ring?

Back 13

Quadratische Matrizen erlauben Addition und Multiplikation mit allen Eigenschaften eines Rings.

Front 14

Bilden die ganzen Zahlen ℤ als (ℤ, +, ·) einen Körper?

Back 14

Nein, nur einen kommutativen Ring (d.h. keine Gruppe bezüglich Multiplikation).

Es fehlen die inversen Elemente bezüglich der Multiplikation. Nur 1 und −1 haben Inverse bezüglich der Multiplikation, die anderen ganzen Zahlen nicht. Multiplikation mit dem inversen Element müsste ja das neutrale Element 1 ergeben. Das geht ausser bei 1 und −1 nur mit Brüchen.

(ℤ, ·) ist also keine Gruppe und deshalb hat zum Beispiel die Gleichung 2x = 1 keine Lösung in ℤ.

Front 15

Bilden die rationalen Zahlen (ℚ, +, ·) einen Körper?

Back 15

Ja! Sogar einen kommutativen Körper.

Front 16

(ℝ, +, ·)
Welche algebraische Struktur?

Back 16

kommutativer Körper

Front 17

(ℤ, +)
Welche algebraische Struktur?

Back 17

kommutative Gruppe

Front 18

(ℂ, +, ·)
Welche algebraische Struktur?

Back 18

kommutativer Körper

Front 19

(ℚ \ {0}, ·)
Welche algebraische Struktur?

Back 19

kommutative Gruppe

Front 20

(ℤ, +, ·)
Welche algebraische Struktur?

Back 20

kommutativer Ring

Front 21

(ℚ, +, ·)
Welche algebraische Struktur?

Back 21

kommutativer Körper

Front 22

Äquivalenzrelation

Back 22

Sei M eine Menge und es sei R eine Relation auf dem Kreuzprodukt M x M, also R ⊆ M x M.
Eine solche Teilmenge R ist speziell und heisst eine Äquivalenzrelation auf M, wenn gilt:

1. Für jedes a ∈ M ist (a, a) ∈ R. Jedes Element muss also äquivalent zu sich selbst sein (Reflexivität).

2. Wenn ein Paar (a, b) in R liegt, dann auch das Paar (b, a). D.h. wenn a äquivalent zu b ist, dann auch umgekehrt (Symmetrie).

3. Wenn wir drei Elemente haben, a, b und c, dann gilt: Falls (a, b) ∈ R und (b, c) ∈ R ist, dann liegt auch (a, c) in R (Transitivität).

Für (a, b) ∈ R sagt man, dass a mit b in einer Beziehung steht. Wenn R eine Äquivalenzrelation ist, dann ist die Beziehung eben speziell, nämlich "a und b sind äquivalent".

Die kleinste Äquivalenzrelation ist die exakte Gleichheit: Ein Paar (a, b) liegt genau dann in R, wenn a = b ist.
Auch die gesamte Menge R = M × M bildet eine (wenig spannende) Äquivalenzrelation.

Front 23

Relationsklasse und Äquivalenzklasse

Back 23

Sei M eine Menge und es sei R bzw. ≈ᵣ eine Relation auf dem Kreuzprodukt M x M. Es sei weiterhin x ∈ M. Dann ist die Relationsklasse [x]ᵣ definiert durch:
[x]ᵣ = { y ∈ M | y ≈ᵣ x }
d. h. die Menge aller zu x in Relation stehenden Elemente.

Falls R eine Äquivalenzrelation ist, nennen wir [x]ᵣ eine Äquivalenzklasse und alle Elemente aus [x]ᵣ heißen zu x äquivalent.
Zwei Elemente von M gehören genau dann zur selben Äquivalenzklasse, wenn sie in der Relation R zueinander stehen.

Gilt eine Äquivalenzrelation R auf einer Menge M, dann schreibt man die Äquivalenzklasse von x als [x]. Sie enthält alle Elemente aus M, die in Beziehung R zu x stehen.
[x] = { y ∈ M | y R x }

Front 24

Eigenschaften von Äquivalenzklassen

Back 24

Sei M eine Menge und es sei R eine Äquivalenzrelation auf dem Kreuzprodukt M x M. Dann

1) bilden die durch R definierten Äquivalenzklassen eine VOLLSTÄNDIGE Aufteilung von M (jedes x ∈ M gehört zu genau einer Klasse)

2) in ELEMENTFREMDE (d. h. disjunkte),

3) NICHT LEERE Teilmengen.

Die Elemente einer Äquivalenzklasse stehen zueinander, aber zu keinem Element einer anderen Klasse in Relation.

Man rechnet mit Äquivalenzklassen, indem man mit einem beliebigen Repräsentanten der Klasse arbeitet.

{engl. equivalence class}

Front 25

Verknüpfung für eine Menge von Äquivalenzklassen?

Back 25

Sei Mᵣ die Menge der Äquivalenzklassen, die in M durch eine Relation R gebildet werden.
Sei M eine Menge mit einer Verknüpfung ♦.
Die Verknüpfung ♦ ist eine wohldefinierte Verknüpfung auf der Menge der Äquivalenzklassen Mᵣ wenn gilt:

[x]ᵣ ♦ [y]ᵣ = [x ♦ y]ᵣ

[Die Verknüpfung ♦ respektiert die Relation R bzw. deren Äquivalenzklassenbildung.]

Front 26

Was haben Äquivalenzklassen mit Brüchen zu tun?

Back 26

Jeder Bruch könnte als Zahlenpärchen (m, n) dargestellt werden. (3, 9), (2,6), (1,3) würden zur gleichen Äquivalenzklasse gehören und (1,3) wäre der typische Repräsentant.
Das wäre eine Lösung für die Problematik der Repräsentation von Float Zahlen auf Computern.

Front 27

Nullteiler eines Ringes

Back 27

Ein Nullteiler eines Ringes R ist ein Element a ≠ 0, für welches es ein Element b ≠ 0 gibt, so dass gilt:
a · b = 0
(b ist immer auch Nullteiler, erfüllt ja die gleichen Bedingungen wie a)

Beim Rechnen mit Restklassen mod 6 (ℤ₆) gilt z.B:
[2]₆ · [3]₆ = [0]₆
Man multipliziert zwei Elemente, die ungleich 0 sind, und erhält als Ergebnis 0. Die beiden Elemente [2]₆ und [3]₆ sind Nullteiler. Die algebraische Struktur (ℤ₆, +, ·) hat also Nullteiler.

Zum Nachvollziehen der Bezeichnung "Nullteiler" kann man 2 · 3 = 6 in ℤ betrachten: Da wären 2 und 3 "Sechsteiler", da beide 6 teilen.

Front 28

Einheiten eines Rings

Back 28

Elemente, die ein Inverses bezüglich der Multiplikation haben, nennt man Einheiten eines Rings. Sie sind der Gegensatz zu Nullteilern.

In einem Restklassenring ℤᵤ gibt es ausschließlich Nullteiler oder Einheiten: Die Restklassen aller Zahlen 0 ≤ k < u, welche teilerfremd zu u sind, sind die Einheiten. Alle übrigen Elemente sind Nullteiler.

Front 29

nullteilerfrei

Back 29

Ein Ring R heißt genau dann nullteilerfrei, wenn aus
  a · b = 0
stets folgt:
  a = 0 oder b = 0

Ring: Kann nullteilerfrei sein, muss aber nicht.

Körper: Ist immer nullteilerfrei (eine seiner wichtigen Eigenschaften).

Ein Restklassenring ℤᵤ ist genau dann nullteilerfrei (sogar ein Körper), wenn u eine Primzahl ist. In dem Fall taucht die 0 in der Multiplikationstabelle nur dort als Resultat auf, wo die 0 selbst beteiligter Faktor ist.