![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
205 Cards in this Set
- Front
- Back
|
Define: Ecology
|
Study of Ecosystems
|
|
|
Population
|
Group of individuals of one species in one area
|
|
|
Community
|
Species which occur together in space and time
|
|
|
Why are is it important to define your definitions of Ecology, Population and Community?
|
The often defined very arbitrarily and it is essential to be clear in your study so that it can be applicable for another study.
|
|
|
What is a model?
|
An abstraction of reality.
Includes componants of interest Relationships of interest There is no single best model because situations changes |
|
|
What did Einstein say about simplicity?
|
"Make everything as simple as possible, not simpler."
|
|
|
What are the two types of models?
|
Mathmatical-Computer
Physical-Pictoral |
|
|
Physical Model
|
Building scale models to help interpret and promote the success of a project. (Example with blue printers and modelers in the floor below)
|
|
|
Pictoral Model
|
Incredibly powerful tool for communication
Visual expression of model Makes elements of model very clear |
|
|
Purpose of a model
|
Describe
Communicate Predict Make Decisions Understand Defend Decisions |
|
|
How are models used in defending a decision?
|
The analyst is able to document their rational and thinking process which led them to the decision and if it doesn't work out then their is guidence for the next trial.
|
|
|
How are models a good substitute for experiments?
|
1) If the species is endangered and the risk is too high it is better to simulate the experiement where possible.
2) Things of high monetary value are difficult to convince people to change for the sake of an experiment. It is better to simulate in this case. |
|
|
How do models help formulate hypotheses?
|
Models can be used to test hypotheses and predict results.
|
|
|
Sensitivity Analysis
|
Identifying Key Componants of a Model
Parameters in a model which do not have much leverage on accuracy are not worth the money and time to put in the model. |
|
|
Analytical Model
|
Able to solve directly for an answer
|
|
|
Simulation Model
|
Solved Repetedly to get an answer
|
|
|
Dynamic Model
|
t shows up as a subscript - there is an explicit time componant
|
|
|
Static Model
|
E=MC squared
|
|
|
Empiracle Model
|
Summarizes relationships with no regard for the mechanism
- a stastical model particularly a linear regression model is an example of this -it describes the data, not the rationale |
|
|
Mechanistic Model
|
Explicity includes mechanism
|
|
|
Stochastic Model
|
Includes parameters for randomness
|
|
|
Deterministic Model
|
Single predicted outcome
Repeatable results |
|
|
Non Spatial Model
|
No parameters for space
Tree model with just Nt |
|
|
Spatially Explicit Model
|
Precise location
Tree example with Nt and x and y |
|
|
Spatially Implicit Model
|
Doesn't specify specific location
Only provides information about parameters relative to each other |
|
|
Discrete Model
|
Time passes in "chunks"
Precces occur as events at distinct times followed by intervals when notheing happens |
|
|
Coninuous Model
|
The change in t is infentessimally small
Processes occur continuously |
|
|
Discrete Exponential Growth Model Formula
|
Also known as the Difference Model
Difference between births of one year to the next Nt+1=Nt+Ntb Where the population next year equals the population now plus the number of babies born (product of # of individuals times birth rates) |
|
|
Continuous Model Formula
|
dN/dt=rN where the change in N with a very small has some % impact on N
|
|
|
Intrinsic Rate of Increase
|
The ability of the species to concert that extra energy (aquired by extra food) into enhaced fecundity and diminished mortality
|
|
|
Fecundity Rate - Explaination and Formula
|
Birth Rate
Number of female babies born per female per time (usually 1 year) |
|
|
Mortality Rate
|
Number of animals which die at time t
|
|
|
IFD Conclusions
|
Prediction 1 doesn’t hold true, while prediction 2 does
|
|
|
Habitat Matching Rule Formula
|
If S1=S2
Then E1/N1=E2/N2 Therefore N2/N1=E2/E1 Where N is population and E is energy intake |
|
|
Habitat matching rule definition
|
It is a surrogate method for determining fitness for an organism based on habitat use
The habitat with more “fish” will have more food |
|
|
IFD Prediction 2
|
“Habitat Matching Rule”
|
|
|
IFD Prediction 1
|
When all habitats are occupied the mean suitability across all habitats should be identical
|
|
|
Basic Suitability
|
Fitness level before any other organism enters area
|
|
|
IFD Model Parameters
|
Si=Bi-Fi(Di)
Suitability for individuals is determined by basic suitability minus some function of density dependence AKA decreasing effect of density |
|
|
“Ideal Assumption”
|
Perfect Information
|
|
|
Assumptions of Fretwell and Lucas
|
Organism will select habitat
This is an evolved trait Suitability of any habitat will decrease as a function of density Allee Effects aren’t included Organism will only settle in most suitable habitat (Which gives highest fitness) Assume al individuals achieve same fitness Organism free to enter any habitat If all assumptions are true than will see IFD |
|
|
Habitat suitability
|
“goodness” or contribution to gene pool of future generations
|
|
|
Distribution
|
# or proportion of individuals in each habitat
|
|
|
Example of habitat discrimination
|
H1: Low food, high predation
H2: High food, low predation |
|
|
Habitat Assumptions
|
Habitats may vary in physical and biological features which contribute to survival
Organisms have the ability to differentiate between god an bad habitats |
|
|
Habitat
|
Portion of earth’s surface where and organism colonizes and lives
|
|
|
Three Hypotheses of IFD
|
1) Territoriality may be a mechanism for distribution
2) Territoriality may be a modifier for distribution patterns – an add on 3) Territoriality may be a way of preserving distribution but not a motivator for it |
|
|
Home Range
|
An area where an organism spends most of its time
|
|
|
Territoriality
|
Conspecific behavior interactions dealing with conspicuousness
|
|
|
What question does IFD answer?
|
Why are organisms where they are at what time
|
|
|
What does IFD stand for?
|
Ideal Free Distribution
|
|
|
Who developed the IFD
|
Fretwell and Lucas 1970
|
|
|
Fitness
|
Maximizing survival and reproduction
|
|
|
What in general have we not considered for the models we have used thus far?
|
The organism’s fitness level
|
|
|
What assumptions have been made in Schoener model 2?
|
Assumed energy intake was the same for all animals
|
|
|
What assumptions have been made in Schoener model 1?
|
We assumed all animals breed
|
|
|
What is important about the way organisms are distributed?
|
This info can inform us about their decision making process and aid in making predictions
|
|
|
Then why was the development of metapopulations “good”?
|
Helped inspire interest in dispersal
Helped people understand local extinctions better Acknowledged it was difficult to assess habitat quality |
|
|
What is the downside of metapopulations?
|
People can argue that extinction is natural
They also don’t manage for biodiversity |
|
|
Describe the source sink
|
One or a few “large” patches feeding into many “small”patches where lambda in the large patch is >1 and in the small patches it is <1
|
|
|
Rescue Effect
|
Effect of overflowing source population recolonizing recently extinct metapopulation
|
|
|
Who developed the source sink model AKA the Core-satellite distribution?
|
Doak and Mills 1994
|
|
|
Who developed the idea of metapopulations?
|
Levins 1969
|
|
|
What is Levin’s metapopulation equation?
|
dp/dt = m p (1 - p) - e p ,
where p is the proportion (fraction) of population centers (e.g., habitat "islands" or patches), m is the migration (colonization) rate, and e is the rate at which local populations go extinct. At equilibrium p* = 1 - e/m. The metapopulation will persist (i.e., p* > 0) only if e < m. |
|
|
Example of Fugitive Species
|
Fireweed
|
|
|
Fugitive Species
|
Species which have evolved to exploit fragmented niche (but not dominate – invasive species
|
|
|
In the metapopulation model local Extinction Events are followed by
|
Re-colonization
|
|
|
Examples of Fragmentations
|
Roads, Agriculture, Forestry
|
|
|
Metapopulation
|
Ensemble of interacting populations which each have a finite life
|
|
|
Fragmentation
|
Previously continuous landscape divided into patterns surrounded by inhospitable matrix
|
|
|
What can we determine with Schoener’s mechanistic model?
|
N* or K
|
|
|
Limitations with Schoener Model 2 Graph
|
Doesn’t make sense for range which has very few individuals in it because unlimited babies cannot occur
|
|
|
Schoener Model 1 (synonym)
|
“Time Limitation Model”
|
|
|
Common Reactivity Field in Africa
|
Watering Hole
|
|
|
Schoener Model 2 (synonym)
|
"Energy Limitation Model"
|
|
|
Intraspecific Interference Competition
|
There is a cost associated with interacting with conspecifics
|
|
|
Logistic Continuous Formula
|
dN/dt=rN(1-N/K)
|
|
|
Why does the logistic model work? Schoener Reason 2
|
Logistic model is just a convenient “good fit” for lots of empirical data sets
|
|
|
Why does the logistic model work? Schoener Reason 1
|
It is a literal representation of the biological process resulting in population growth
|
|
|
Empirical Models
|
Summarizes relationships with no regard to mechanism
|
|
|
Schoenor 1973 sought to answer what question?
|
Why does the logistic model work?
|
|
|
Schoenor
|
“Shaner”
|
|
|
Wide variety of models based on the logistic model occur when the following assumptions are manipulated:
|
Competition
Resource Acquisition Time Allocation Resource Availability |
|
|
Problems with “Road Kill Science”
|
Limited by type of death
(Easy sampling though) |
|
|
Problems with following the entire cohort
|
Determining Mortality
Environmental Stochasticity Length of time required to wait may be very long |
|
|
Problems with Mark-Recapture Method
|
Determining Mortality
Difficult to judge age |
|
|
How do you measure survivorship?
|
Mark-Recapture
Follow an entire cohort throughout their life cycle “Road Kill” Method |
|
|
Graphical Lambda =
|
Plot LnN vs T
e^r (slope) |
|
|
Graphical Method for simulating Lambda collapse
|
Determining stable age structure through simulation
Pick initial starting population values Iterate until reach stable age structure |
|
|
Two methods for Lambda collapse
|
Graphical
Analytical |
|
|
If Lambda <1
If Lambda=1 If Lambda>1 |
Negative exponential growth
0 net growth Exponential growth |
|
|
Lambda
|
Discrete per capita rate of growth of a population
|
|
|
Age/stage class models generally model F or M?
|
Females although, males have a lower r if they are a trophy species
|
|
|
Assumptions of the Discrete Model
|
Time passes in chunks
Same lambda for all individuals Lambda doesn’t change with environment or density No emigration or immigration |
|
|
Age or Stage class models
|
Models used to describe populations where different age (stage) individuals have different probabilities of dying, giving birth etc.
|
|
|
Recommendations for avoiding the pitfalls of pseudorandomness
|
Look up seed
Use good seeds Never trust RNG (look up) Use multiple RNGs Describe your RNG method |
|
|
Seed
|
Method of instructing where RNG begins from
|
|
|
Pseudorandom
|
RNG always begins from the top/or same number in its list
|
|
|
Example of RNG
|
RANDBETWEEN function in excel
|
|
|
RNG
|
"Random Number Generator”
|
|
|
POO
|
Probability of Occurrence
|
|
|
Continuous Probability
|
Value can be any within a particular range
|
|
|
Binomial Probability
|
A and B Events
|
|
|
Example of Discrete Probability
|
1 or 2 pine cones, or 2.2 and 3.2 (Nothing in between)
|
|
|
Discrete Probability
|
Events which can take only particular values
|
|
|
Two classes of probability
|
Discrete and Continuous
|
|
|
Significance of Independent Sample
|
Important to determine randomness so one can know whether or not to treat samples independently
|
|
|
Example of up and down random test
|
Stock market
|
|
|
Example of test for randomness
|
computer evalutes output for patterns
|
|
|
1-D Random Numbers
2-D Randomness 3-D Randomness |
Time or Space
Time and Space (Raindrops on paper) x and y X,Y,Z |
|
|
“Gamblers Fallacy”
|
Current events are not influenced by previous outcomes
|
|
|
Random Number
|
With out aim definition or direction
|
|
|
Example of Genetic Stochasticity
|
Fur color changes
|
|
|
Genetic Stochasticity
|
Random changes in gene frequencies (Not natural selection)
|
|
|
Example of Natural Catastrophes
|
Example of Natural Catastrophes Fire, Hurricane
|
|
|
Natural Catastrophes
|
Infrequent but devastating events experienced by all individuals
|
|
|
Example of Environmental Stochasticity
|
Summer weather variation
|
|
|
Environmental Stochasticity
|
Random events experienced similarly by all individuals (Frequent)
|
|
|
What is an example of demographic stochasticity?
|
Luck at finding food, parental skills, nest making materials etc.
|
|
|
Demographic Uncertainty
|
Random events experienced differently for different individuals
|
|
|
What did Shaffer proposed occurred in natural systems?
|
That there were four sources of uncertainty: Demographic, Environmental, Genetic and Natural Catastrophes
|
|
|
It is more realistic to have a range of predictions because_______
|
There is uncertainty in the real world
|
|
|
Even though there is geometric growth, ___ can still vary.
|
R
|
|
|
Deterministic
|
Having a single predicted outcome
|
|
|
what are two ways that models have been used in the management of wildlife populations?
|
a) The control of populations which are of socioeconomic concern
b) The conservation of endangered species |
|
|
State in your own words the problem raised by Beissinger and Westphal (1998) with the way models are used.
|
The problem Beissinger and Westphal pointed out is that these PVA models are being used without any regard to the specifics of the population characteristics. Density dependence is not being taken into account among other things. The PVA models are also being used without first determining which type of model explains the observed patterns the best.
|
|
|
What is the equation for the discrete geometric growth model?
|
a. Nt+1=Nt+rNt
|
|
|
Write a new version of the discrete geometric growth model that includes the removal of y% of the rhinos each year
|
b. Nt+1=(Nt+rNt)-y%Nt
|
|
|
What is the equation for the discrete logistic growth model?
|
Nt+1=Nt+Ntr(1-Nt/K)
|
|
|
Write a new version of the discrete logistic growth model that includes the removal of y% of the rhinos each year.
|
Nt+1=Nt+Ntr(1-Nt/K)-y%Nt
|
|
|
is the equation for the discrete fowler growth model?
|
Nt+1=Nt+Ntr(1-(Nt/K)^n))
|
|
|
Write a new version of the discrete fowler growth model that includes the removal of y% of the rhinos each year.
|
Nt+1=Nt+Ntr(1-(Nt/K)^n))-y%Nt
|
|
|
State in your own words why the Fowler version of the model would be used instead of the logistic model.
|
The fowler version involves adding the exponent n to the growth rate parameter of the model to account for the heavier effect of density dependence among larger animals in the real world.
|
|
|
What are two things that could be done to decide which of these models was “best”
|
A . Use correlation coefficients to evaluate which model has the best “fit” and use for comparison.
B. Compare growth rate with body of scientific knowledge/historical observations to determine if the growth rates are biologically possible for this type of organism. |
|
|
, we saw that we could use calculus to integrate this equation and derive the following analytical solution:
|
N(T) = N(0)erT
|
|
|
continuous geometric growth” model:
|
dN/dt = rN
|
|
|
Fortunately, there are several”tricks” for approximating the population trajectories using these differential equations. The one we will use is called
|
Euler’s Method
|
|
|
Euler’s Method
|
Nt+h = Nt + (dN/dt) * h
|
|
|
) What is the equation to describe the Euler approximation to the continuous geometric growth model
|
Nt+h = Nt + (rN) * h
|
|
|
So to get a better approximation, should h be larger or smaller? Why
|
A smaller h is better because it takes into account more infinitesimally small time increments which bring it closer to representing a continuous function, or its exact analytical counterpart.
in other words, the slope dN/dt gets calculated more frequently |
|
|
In class, we talked about 8 reasons why population growth rate could be density dependent
|
• Aggression
• Food Scarcity • Predators concentrate efforts more • Disease • Interference (Eating etc) • Limited living space • Predators learn better methods for killing prey • Immigration declines • Emigration increases |
|
|
What is the analytical solution to the differential equation that describes continuous geometric growth
|
N(T) = N(0)erT
|
|
|
Give two sentences describing the potential problem with the North Sea cod stock as presented by the authors with respect to the current (as of 1997) fishing practices.
|
a. The current exploitation regime is unsustainable.
b. Even managing for the maximum sustained yield may be unsustaible because of the inherent risks in the system. |
|
|
Based on the gain curve, what is an appropriate model to describe the population dynamics of the North Sea cod stock (without fishing)? Write the discrete form of this model.
|
The Logistic growth Model Nt+1=Nt+RNt(1-Nt/K
|
|
|
What is N* (the equilibrium population) for this population (take a look at your class notes) if the carrying capacity of the cod stock is 400 and the discrete growth rate is 1.5?
|
RNt(1-Nt/K) = 0
1-Nt/K=0 -Nt/K=-1 -Nt=-K Nt=K Nt=400 |
|
|
First, create a graph showing Nt+1 vs. Nt for your equation in question 3. Draw the line on this graph where Nt+1 = Nt. At what population size do the two curves cross? What does this intersection represent?
|
They cross at (400, 400)
This represents N* or the equilibrium point in the model |
|
|
In class, we talked about an experiment where we repeatedly drew numbered billiard balls from a hat, recorded the number on the drawn ball, then replaced them in the hat (a “with replacement” style of sampling). Explain in you own words why the “without replacement” version of the same experiment is not random
|
If you don’t add the billiard balls back into the drawing then the odds of drawing another ball increases because the pool which you are drawing from is constantly decreasing in size. The outcome of the first drawing provides information for the next drawing.
|
|
|
Consider a sampling scheme where a master’s student swims the length of a transect parallel to a beach and counts the number of tuna at 50 meter intervals. List three reasons why the fish counts recorded from this sampling might not be random.
|
a. The student may choose to sample at a certain angle as they are swimming because it is more convenient physically for them to do so.
b. The student probably won’t be able to sample at exactly every 50 meters because they will be focused on trying to actually swim. (It just isn’t very precise) c. Most likely the swimmer will be constrained in his/her attempt to swim by physical barriers etc. The swimmer will probably only be able to swim along a beach in areas which are suited for human swimming. Therefore this wouldn’t be a random sampling of fish because the location of the observations is not random. |
|
|
) What are three examples of demographic stochastic processes that affect baby birds in a nest?
|
a. Parental nurturing skills
b. Parent’s luck at finding food c. Parent’s luck finding nest building materials |
|
|
What are three examples of environmental stochastic processes that affect mosquitoes in a field?
|
a. Dry summer – no water to breed in
b. Daily variation in wind/rain – drowning/ unable to feed on prey c. Lack of prey due to random poor growing conditions for prey’s food |
|
|
What are three examples of catastrophic stochastic processes that affect fish in a pond?
|
a. Severe Drought – to the extent that the pond actually decreases in volume substantially
b. Hurricanes –could potentially clog up ponds with DWD (dead woody debris) or destroy them through flooding c. Volcanic eruptions – depositing ash and debris in to the pond |
|
|
Think about the length of each fish counted along the transect from question 2. Would you represent the frequencies of these lengths as a discrete or continuous distribution? Why
|
It is a conintuous distribution because the values could be any value between some minimum and maximum set of values.
|
|
|
Think about the number of berries today on each bush on the south face of Cypress Mountain. Are the frequencies of these berry counts best represented by a discrete or continuous distribution? Why
|
They are best represented by discrete frequencies because the berries that are being counted in whole unit increments. If they were being monitored constantly by some automated machine and counted veeeerrryyy slowly as they were growing..that would be continuous.
|
|
|
What type (uniform or discrete) and class (uniform, normal, something else) of probability distribution would you expect if you were to record the sum of two six sided dice thrown 100 times? Sketch it out.
|
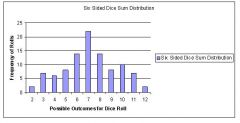
a. This is a discrete distribution because there are 6 distinct outcomes and no outcome can fall in between these predicted outcomes. (I am not sure what to do if the dice somehow lands on a vertex.)
b. This is definitely not a uniform or normal distribution. It is a something else which has discrete occurrences ranging from a few on the ends like 2 and 12 to a lot in the middle. The number six for example has multiple ways of adding up to equal it so it will have a higher frequency than 2 or 12. It is a pyramidal distribution |
|
|
What are the two potential risks to the persistence of the park rhinos?
|
a. Poaching
b. Reduced Carrying Capacity due to loss of habitat |
|
|
The model presented in the Rhino paper described as a “stage class” model (i.e., not an age class model). Why?
|
This is a stage class model because the classes being modeled are not based on age but based on the developmental stages (calves, subadults and adults) which are characteristic of the Indian rhino.
In addition, the oldest class could be any age over 7 and can die at any age interval |
|
|
Explain the following difference equation in words:
a. n1(t)=n3 (t-1)*S0*b3*f b.n2(t)=n2 (t-1)*S1 c.n3(t)=n2 (t-1)*S2+n3 (t-1)*S3 |
a) is the number of baby rhinos which survive to be age class 1 (rhinos only give birth at age 3 apparently)
b)The number of rhinos at age class 1 which survive to be age class 2 c) The number of rhinos at age class 2 which survive to be age class 3 and the number of age class 3 rhinos which survive in age class 3 |
|
|
Write this in matrix notation:
a. n1(t)=n3 (t-1)*S3*b3*f b.n2(t)=n2 (t-1)*S1 c.n3(t)=n2 (t-1)*S2+n3 (t-1)*S3 |
n1(t) 0 0 b3*f*S3 n1(t-1)
n2(t) = S1 0 0 x n2(t-1) n3(t) 0 S2 S3 n3(t-1) |
|
|
How would you define carrying capacity in your own words?
|
Carrying capacity is the maximum number of organisms (at a given growth rate and survivorship) that the environment can support without incurring negative density dependent losses.
...and carying capacity is not always the equilibrium point In addition, net growth is at zero |
|
|
Why would you press the F9 key if you were using your model to make predictions?
|
The random numbers change and the trajectory fluctuates. You would press the F9 key in order to see how much the trajectory varied. It would be useful to identify the max and min points in the trajectories in order to develop estimates which encompassed all prediction possibilities of stochasticity effects.
|
|
|
Now one last change to simulate the effect of poaching...
Have you added environmental or demographic stochasticity? |
This is environmental stochasticity because fluctuations in loss due to poachers are experienced by all individuals as the pass into that stage class.
|
|
|
So what is the general effect of poaching predicted to be on the rhinos (according to study)?
|
Poaching appears to have the most detrimental effect on the rhino population compared with perhaps environmental stochasticity effecting carrying capacity.
It reduces the average equilibrium density which exaggerates the fluctations. |
|
|
What is the point of REM 611?
|
To be able to help resource managers or become resource managers use models to:
Predict Understand Make Decisions |
|
|
We do we use models for as Remmers?
|
Describe
Predict Protect Promote Harvest Understand Communicate |
|
|
What are some challenges?
|
Variation
Population Communities Ecological and Social Sciences are linked and can't be treated in isolation |
|
|
What do Resource Managers Do:
|
a. Track populations
b. Interested in changes in size for the population c. We want to know if pop numbers are going up or down d. Tourism, pests, endangered species |
|
|
Define a BIDE model
|
Birth and Immigration minus Death and Emigration determine population size
|
|
|
Geometric Growth Model Formula
|
Nt+1=Nt+RNt
|
|
|
What is R?
|
R is the growth rate or births minus deaths
|
|
|
Assumptions of the geometric growth model:
|
a. Discrete Growth
b. All individual are identical c. They all contribute births equally d. They have equal lambda e. Lambda never changes f. N can be non integer g. No I or E h. closed population i. Geometric Growth: R= B-D |
|
|
Analytical Solution for the geometric growth model:
|
Nt=λ^t*N0
|
|
|
Logistic Model Definition
|
Includes negative feedback from density dependence
Includes parameter for carrying capacity |
|
|
Negative Feedback examples
|
a) Density Dependence - food loss
b) Interference - animal interactions, mates, feeding habits c) Living Space d)Aggression e)Predators increase and concentrate efforts f) Predatorslearn evasion techniques because there are more opportunities to learn g) Immigration declines h) Emigration increases |
|
|
Logistic Model assumptions
|
Introduced density dependence
Assumes growth rate is negative linear function of Nt |
|
|
What is the general shape of a logistic curve?
|
sigmoid
|
|
|
Coninuous Logistic Growth Model List the Analytical Solution and Graphical Solution
|
dN/dt
Eulers approximation : Nt+1= Nt+(RN) h |
|
|
What are 2 factors Malthus hypothesized influenced population size?
|
DI:
Random: fire, floods Constant: hunting |
|
|
Allee Effects
|
Problems faced by small populations such as finding mates, foraging efficiency, protection from predators and inbreeding problems
|
|
|
Deterministic
|
Always the same, every time we run a model it is the same prediction
|
|
|
Stochastic
|
Introduction of random variables
|
|
|
Equilibrium
|
Population does not change over time
Continuous Model: dN/dt=0 Discrete Model: Nt+1=Nt, Nt+1-Nt=0 |
|
|
Stability of a population:
|
Tendency of system to return to its equilibrium state following a perturbation from that state
|
|
|
Global Equilibrium:
|
Returns to equilibrium point no matter how hard we push
|
|
|
Local Equilibrium:
|
Returns to equilibrium point, but this point is at a different position than the initial starting point
|
|
|
Resistance Equilibrium
|
resistance to leaving equilibrium
|
|
|
Resilience
|
speed with which system returns to former stat after a disturbance
|
|
|
What are 3 factors used in regulating a Fish Pond?
|
-increase food
-decrease death rate (use less effective tackle) -increase size of pond |
|
|
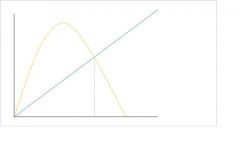
Describe a fishing pond with regulation.
|
Loss
Growth EQ Limitation: (DD) -Higher death rate will have a steeper line -Density DD growth and DD loss -But there is a point where growth balances loss -Higher r makes the curve pointer |
|
|
Describe fish pond with low death
What happens if add food? How about changing the size of pond? |
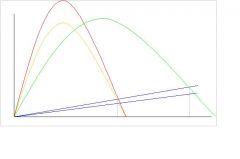
changed tackles
if d is low already…managing for d doesn’t do much population is insensitive to d try to add food…nothing happens Change size of pond! Very Responsive |
|
|
Describe a fish pond where there is initial high death
What happens when death decreases? Changing pond size? Changing food? |

Decreasing death has a huge impact
Changing pond size had negative effect Increasing food didn’t help (K) |
|
|
Limitation Formulaic Representation
|
Nt+1 – Nt= 0
and dN/dt=0 |
|
|
Describe Discrete Testing for Equilibrium (Geometric)
|
Nt+1=Nt+RNt where R is discrete per capita growth
If Nt+1-Nt=0 then Solve for Nt …Nt+1-Nt=RNt 0=RNt Nt=0 |
|
|
Numerical Testing for Equilibrium (Geometric)
|
find N*
Set up model on computer perturb system (move little up or down…local stability) A lot up or a lot down is for global stability |
|
|
Rickor Diagram – Graphical Approach (Geometric)
Describe derivation - |
Nt+1=Nt+RNt
Nt+1=(1+R)Nt +0 This is a line Y= mX+B R=birth-deaths If R(t) then the slope is >1 |
|
|
Describe the Discrete Logistic Equilibrium Approach (Analyitical)
|
Nt+1=Nt+RNt(1-Nt/K)
Nt+1-Nt=0 Equilibrium Nt=1-Nt=RNt(1-Nt/K)=0 Now solve for Nt Nt=K But we knew that already |
|
|
Describe the Rickor Diagram Logistic
|
Nt+1=Nt+RNt(1-Nt/K) Solve for line
Nt+RNt-R(Nt^2)/K This is the equation for a parabola |
|
|
Is a two point stability cycle stable?
|
It is not globally stable
|
|
|
Is there a graphical way of determining eq for a Continuous Models ?
|
No, only simulation or anylitical
|
|
|
Neighborhood Stability Analysis (Only local stability test for)
Formula: |
dN/dt=F(N)
|
|
|
Perturbation over time for a continuous model
Formula: |
Perturbation = N*+x
N* is our equilibrium What happens if we push population a small distance away from N*? Small distance is represented by x |
|
|
Perturbation over time for a continuous model
Formula: |
So Perturbation over time= N(t)=N*+x(t)
|
|
|
So Perturbation over time= N(t)=N*+x(t) (in a continuous model)
Calculus formula: |
How does x change over time? dx(t)/dt?
|
|
|
For a continuous model:
a=∂F(N*)/∂N* in the formula -> dx(t)/dt=ax(t) Describe the outcome of a: |
a<0, then locally stable and perturbation is lessening over time
a>0, than perturbation is increasing and is not stable a=0, then never changes over time and is neutrally stable |
|
|
Paradox of Enrichment
Describe: |
lets assume this can be modeled with logistic discrete model
Outcome is that population becomes less stable when increasing population (Comes to a two point stable limit cycle) When r gets higher and higher we get more and more limit cycles until eventually there will be chaos |
|
|
regulation
|
forces that bring population back to their equilibrium
|

