Reading...
Play button
Play button
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
17 Cards in this Set
- Front
- Back
Divergence of a gradient
|
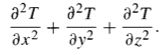
Laplacian
|
|
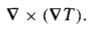
Curl of a gradient
|
= 0
|
|
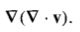
Gradient of Divergence
|
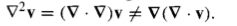
Seldom occurs. Not the same as Laplacian of a vector
|
|
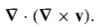
Divergence of a Curl
|
= 0
|
|
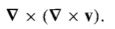
Curl of a Curl
|
|
|
|
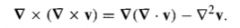
Fundamental Theorem for Gradients
|
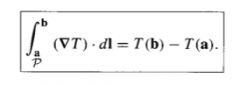
(Ignore the P)
- Independent of the path taken from a to b - Closed integral = 0 |
|
|
Fundamental Theorem for Divergences
|
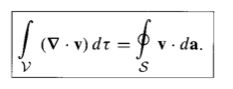
aka "Gauss's Theorem, Green's Theorem, or Divergence Theorem"
|
|
|
Fundamental Theorem for Curls
|
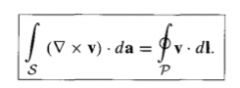
"Stokes Theorem"
- the cross part depends only on the boundary line, not on the particular surface used. - closed integral for cross part equals zero for any closed surface |
|
|
An example of a 3D Dirac-Delta Function
|
|
|
|
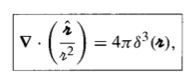
Helmholtz Theorem
|
Any field can be uniquely determined by it's divergence and curl and knowing it's boundary conditions
|
|
|
Irrotational (Curl-less) Fields Theorem
|
|
|
|
Solenoidal (Divergence-less) Fields Theorem
|
|
|
|
Coulomb's Law of Electric Fields
|
|
|
|
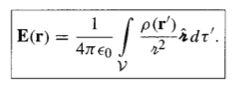
Gauss's Law
|
|
|
|
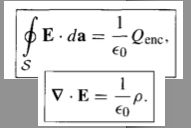
Electric Potential
|
|
|
|
Poisson's Equation
|
|
|
|
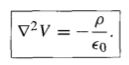
The Triangle Diagram based on the three fundamental quantities of electrostatics
|
|
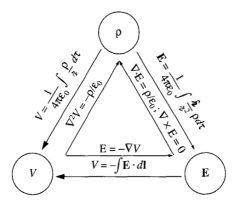
