![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
10 Cards in this Set
- Front
- Back

|
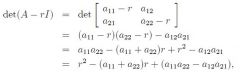
|
|

|

|
|

|
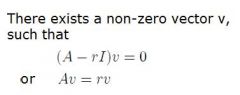
|
|

|
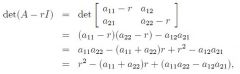
|
|

|
|
|

|
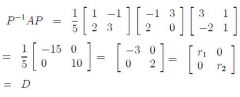
|
|
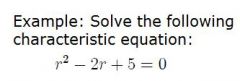
|
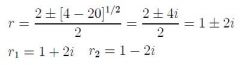
|
|
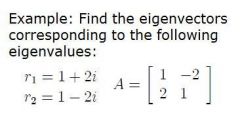
|
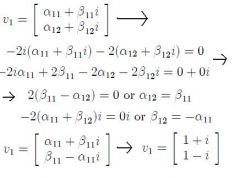
|
|
|
What is an eigenvalue?
|
An eigenvalue of a square matrix A is a number r that, when subtracted from each of the diagonal elements of A, converts A into a singular matrix. Since A is singular iff its determinant is zero, we can calculate eigenvalues fo A by solving the characteristic equation:
det(A-rI) = 0, where I is the identity matrix and det(A-rI) is the characteristic polynomial of A. |
|

|

|

