![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
103 Cards in this Set
- Front
- Back
|
A product of two or more integers is even if at least one of its factors is ____
|
even
|
|
|
If no factor is even then the product is
|
odd
|
|
|
When adding and subtracting integers, two even integers or two odd integers will be ____
|
even
i.e. 3+3 = 6 (two odd integers) 9-5 = 4 (two odd integers) 10-4 = 6 (two even integers) 10+2= 12 (two even integers_) Results are always even |
|
|
In the case of one even and one odd, their sum and difference will be _____
|
odd
ie. 3 + 4 = 7 (one odd and one even) 4 - 3 = 1 |
|
|
What is prime number?
|
An integer with precisely two distinct positive factors, 1 and itself.
i.e. 2, 3, 5, 7, 11, 13, 17. However, 21 is not a prime number because it is only divisible by 1,2,7 and 21. Remember that 1 is not a prime number-it has only one positive factor. |
|
|
All integers greater than 1 will be either prime numbers or numbers that can be expressed as a product of prime factors.
What are the prime factors of: 15 92 363 |
15: 5*3
92: 2*2*23 363: 3*11*11 |
|
|
How can CONSECUTIVE INTEGERS be expressed of this set {...-2, -1, 0, 1, 2, 3, 4...}?
|
n, n+1, n+2, n+3, n+4
|
|
|
How can CONSECUTIVE EVEN INTEGERS be expressed of this set { 0, 2, 4, 6, 8,....}?
|
2n, 2n+2, 2n+4, ....
|
|
|
How can CONSECUTIVE ODD INTEGERS be expressed of this set {1,3,4,5,7,9,...}?
|
2n+1, 2n+3, 2n+5,...
|
|
|
Rules of Real numbers:
1. a + b = ab = 2. (a+b)+c = and (ab)c = 3. a(b+c) = 4. a+b and ab are positive if both ... 5. a+b is negative if ... 6. ab is negative if 7. a=0 or b=0 if ab = 8. |a+b| <_ |a|+|b| ex. If a=12 and b=3 then... and if a =12 and b=-3 then... |
Rules of Real numbers:
1. a + b = b+a ab = ba 2. (a+b)+c = a+(b+c) and (ab)c = a(bc) 3. a(b+c) = ab + ac 4. a+b and ab are positive if both ...a and b are positive 5. a+b is negative if ...b is negative or visa versa 6. ab is negative if either or are negative 7. a=0 or b=0 if ab = 0 8. |a+b| <_ |a|+|b| ex. If a=12 and b=3 then... and if a =12 and b=-3 then...a|+b| = |9| + 9<15 = |a| + |b| |
|
|
A product of two or more integers is even if at least one of its factors is ____
|
even
|
|
|
If no factor is even then the product is
|
odd
|
|
|
When adding and subtracting integers, two even integers or two odd integers will be ____
|
even
i.e. 3+3 = 6 (two odd integers) 9-5 = 4 (two odd integers) 10-4 = 6 (two even integers) 10+2= 12 (two even integers_) Results are always even |
|
|
In the case of one even and one odd, their sum and difference will be _____
|
odd
ie. 3 + 4 = 7 (one odd and one even) 4 - 3 = 1 |
|
|
What is prime number?
|
An integer with precisely two distinct positive factors, 1 and itself.
i.e. 2, 3, 5, 7, 11, 13, 17. However, 21 is not a prime number because it is only divisible by 1,2,7 and 21. Remember that 1 is not a prime number-it has only one positive factor. |
|
|
All integers greater than 1 will be either prime numbers or numbers that can be expressed as a product of prime factors.
What are the prime factors of: 15 92 363 |
15: 5*3
92: 2*2*23 363: 3*11*11 |
|
|
How can CONSECUTIVE INTEGERS be expressed of this set {...-2, -1, 0, 1, 2, 3, 4...}?
|
n, n+1, n+2, n+3, n+4
|
|
|
How can CONSECUTIVE EVEN INTEGERS be expressed of this set { 0, 2, 4, 6, 8,....}?
|
2n, 2n+2, 2n+4, ....
|
|
|
How can CONSECUTIVE ODD INTEGERS be expressed of this set {1,3,4,5,7,9,...}?
|
2n+1, 2n+3, 2n+5,...
|
|
|
Rules of Real numbers:
1. a + b = ab = 2. (a+b)+c = and (ab)c = 3. a(b+c) = 4. a+b and ab are positive if both ... 5. a+b is negative if ... 6. ab is negative if 7. a=0 or b=0 if ab = 8. |a+b| <_ |a|+|b| ex. If a=12 and b=3 then... and if a =12 and b=-3 then... |
Rules of Real numbers:
1. a + b = b+a ab = ba 2. (a+b)+c = a+(b+c) and (ab)c = a(bc) 3. a(b+c) = ab + ac 4. a+b and ab are positive if both ...a and b are positive 5. a+b is negative if ...b is negative or visa versa 6. ab is negative if either or are negative 7. a=0 or b=0 if ab = 0 8. |a+b| <_ |a|+|b| ex. If a=12 and b=3 then... and if a =12 and b=-3 then...a|+b| = |9| + 9<15 = |a| + |b| |
|
|
What is the trick to converting any decimal to a fraction?
1. 95.3 2. 4.28 3. 0.327 |
Simply remove the decimal point, and put the number over the appropriate multiple of 10
1. 95.3 = 953/10 2. 4.28 = 428/100 3. 0.327 = 327/1000 |
|
|
How do you find what percent of 40 is 8?
|
8/40 = x/100
Because x/100 = %age |
|
|
What are the three ways to represent rations and proportions? Use x and y as your variables
|
x/y
x:y x to y Keep in mind that the order in which the two numbers in the ratio appear is important; they cannot be reversed and have the ratio mean the same thing. |
|
|
What is the definition of proportion? What is the good trick for solving proportions?
|
A proportion in volves ratios. Simply, it is a statement in which two ratios are set equal to each other. A good trick in solving proportions is to CROSS MULTIPLY.
ie. 3/4 = 12/x can be crossed multiplied resulting in 3x = 48. x = 16 |
|
|
How do you calculate the range in this set: 2,3,4,4,4,5,6,9,10,11,11,11,12,14,17
How many modes are there? |
Calculate the range by subtracting the least value in a set from the greatest value.
17 - 2, or 15 There are two modes: 4 and 11 because they appear the most frequently. |
|
|
What are sets?
|
simply, a set is a group of numbers or "elements," (i.e., objects other than numbers). In order to deal with sets on the test, you should know the terminology and notation used to describe them.
|
|
|
How are the number of elements in a set notated?
|
|P|
The set itself is often notated as a list of elements, which do not have to be ordered sequentially. For example, P = {-8, -2, 0, 4} or P = {-2, 3 -8, 0}. In this particular set, |P| = 4 b/c there are 4 elements. |
|
|
If ALL of the ELEMENTS in one set are also elements of another, that set can be called a ______ of the other.
|
"subset"
For example, set P= {-8, -2, 0, 4} is a subset of Q = {-8, -2, 0, 3, 4, 9, 12}. |
|
|
What does the "union" of two sets mean?
|
A "union" of two sets is a set of all of the elements that are in one set, the other set, or both sets.
NOtated: PUQ |
|
|
What does the "intersect" of the two sets mean?
|
An "intersection" of two sets is a set of all of the elements that are in both sets. THis is notated: P (upside down U) Q
|
|
|
If two sets that have no overlap are said to be ...
|
mutually exclusive.
|
|
|
PUQ =
|
|P| + |Q| - |P(upside down U)Q|
|
|
|
What rule applies if the sets are mutually exclusive?
|
|PUQ| = |P| + |Q|
|
|
|
What are three top counting methods that make counting easier?
|
Factorials, permutations, and combinations
|
|
|
What is factorial?
What is the factor rule? |
If an integer n is great than 1, n factorial is equal to all integers from 1 to n multiplied together.
For example: 4! = 1*2*3*4= 24 Another rule is: 0! = 1! = 1 |
|
|
How are factorials often used?
|
to determine the number of different ways that sets can be ordered. For example, consider the number of ways that you can order the letters F, G, and H:
FGH, FHG, GFH, GHF, HFG, and HGF. This is equal to 3!, or 6, and these different orders are called "permutations" of the set of letters. |
|
|
What is a permutation? How can they generally be written?
|
The different orders a set can be arranged. Permutations are processes by which objects are selected one at a time in a specific order.
Generally written: n(n-1)(n-2)...(3)(2)(1)= n! |
|
|
In addition to thinking about ordering, you can think of permutations as selections; what you're really doing is choosing each "set member" one by one, in a specific order. If you want to select only certain set members and not others, you have to use an equation involving a smaller set, noted as ____
|
k
The ways of selecting that subset from the bigger set are called COMBINATIONS and are noted this way: (n over k) |
|
|
How are combinations calculated?
|
The value of (n over k) is calculated this way:
(n over k) = (n! / k!(n-k)!) Basically, this will calculate the number of subsets with k number of elements within a set that has n elements. i.e.: S = {V, W, X, Y, Z}. The number of 3-element subsets of S, or the number of combinations of 5 letters taken 3 at a time is, 5!/ 3!(5-3)! = 120/(3)(2)(2) = 10. So, you can make 10 different groups of 3 letters from the 5 letters in set S. |
|
|
When you are asked to find the number of possible combinations for multiple groups____
|
just multiply the number of possible combinations for each group.
|
|
|
What are the most important probability concepts you'll need to know?
|
1. Experiment: a test that has a specific number of outcomes.
2. Outcome: one possible result of an experiment. An experiment may have multiple possible outcomes. 3. Event: a particular set of outcomes. |
|
|
What is an experiment?
|
1. Experiment: a test that has a specific number of outcomes.
|
|
|
What is an outcome?
|
2. Outcome: one possible result of an experiment. An experiment may have multiple possible outcomes.
|
|
|
What is an event?
|
3. Event: a particular set of outcomes.
|
|
|
EQUATION: For an experiment that has the SAME likelihood for each individual event, the probability of an event X happening is:
|
P(X) = The number of outcomes of X / The Total number of possible outcomes.
i.e. Consider the experiment of rolling 12-sided die. This experiment has 12 possible outcomes (1-12). One possible EVENT is that you will roll a 7 (this is the outcome, which is written inside curly brackets: {7}). Another possible EVENT is that you will roll an even number. There are 6 such outcomes: {2,4,6,8,10,12} (Ryan: this kind of looks like a set). So according to our equation the probability of rolling an even number is: P({2,4,6,8,10,12}) = | {2,4,6,8,10,12}| / 12 = 6/12 = 1/2 |
|
|
Like with permutations, the probability of multiple events occurring calls for multiplying the separate probabilities together.
See example |
The probability of rolling an even number on a 12-sidded die twice in a row is 1/2 x 1/2 = 1/4
|
|
|
PROBABILITY OF DEPENDENT EVENTS: the probability for the "dependent event" will have to be adjusted based on the fraction of the first event.
See example |
For example, if you want to know the probability of choosing 2 red cards out of a 52-card deck, you would multiply the probability of choosing the first card: # of outcomes of red/total # of cards) 26/52 = 1/2 ...multiply this by the probability of choosing a red card out of the same deck without REPLACING the first: 25/51. So the probability of choosing 2 red cars is (1/2)(25/51) = 25/102
AWESOME!! |
|
|
A gumball machine contains only cherry, grape, lemon and orange gumballs in a ratio of 5:4:3:2:1. Which of the following could equal the total number of gumballs in the machine?
|
The actual number of gumballs must be a multiple of the ratio total 5+4+3+1 = 13.
Now you just have to find the answer choice that's a multiple of 13. Answer 52 |
|
|
What is the subtracting 1 rule with probability problems?
|
The probability that an event occurs + the probability that the event does NOT occur must equal 1.
For example if the probability that event A is 65% then the probability that even A does NOT occur is 35%. |
|
|
When do you know that you should use the subtracting 1 rule with probability problems?
|
If a probability question involves multiple scenarios where there are significantly fewer way for an event NOT to occur, you should consider finding the probability that the event does NOT occur and then subtract 1.
|
|
|
THE last digit squared rule.
An amazing trick when trying to narrow down two possible answers. |
"The last digit of the square of an integer x is the same as the last digit of the square of its last digit."
i.e. which one is square root 7744? 88 or 86 The last digit of 88 is 8. Square that, 8^2, you get, 64. Notice the last digit of 64, is 4. Which matches last digit of square root 7744. Square root the last digit in 86. 6^2 = 36. The last digit of 36 is 6. 6 does not match the last digit of sqrt.7744. Choice 88 is the correct answer. |
|
|
What is the trick with this problem?
20% of A = 40% of B = 60% of C = 80% of D; B/D = C/A*x; solve for x. |
Get everything to variable A because A = everything . Once you get everything in terms of A you can plug and chug then cancel out the A's.
|
|
|
WORD PROBLEMS: What are the three steps you should follow when encountering a word problem?
|
1) Determine the math concept being tested.
2) Determine what specific piece of information the question is asking you to find. 3) Look for equations and/or other relationships in the language of the text. |
|
|
What is the Lateral Area of a Cone formula
|
= 1/2cl
(c= circumference) |
|
|
What is the Volume of a cone?
|
1/3 pi r^2 h
|
|
|
What is the SA of a sphere?
|
4Pir^2
|
|
|
What is the V of a Sphere?
|
4/3Pir^3
|
|
|
What is the V of a pyramid?
|
1/3Bh
(B=area of the base) |
|
|
What is the formula for finding the longest point in a rectangular solid?
|
d =Square Root (l^2 + w^2 + h^2)
|
|
|
How do you find the volume of a Uniform Solid?
|
Bh
(B + area of the base) |
|
|
How do you find the volume of a Cube?
|
= e^3
|
|
|
Volume of a cylinder:
|
Pi r^2 h
|
|
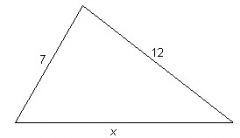
What is are the rules for the Lengths of side?
Solve this. A. 3 B. 5 C. 17 D. 19 E 22 |
1) Any side of a triangle cannot be shorter than the difference of the other two sides.
2) Any side of a triangle cannot be longer than the sum of the other two sides. 7 + x = 12 x = 5 ( so we know that the answer can't be shorter or equal to 5) 7+12 = 19 (We know that x cannot be longer than 19) C is the answer. |
|
|
What are the three main trigonometry identities that you should be aware of?
|
sin^2 x + cos^2 x = 1
tan^2 x + 1 = sec^2 x 1 + cot^2 x = csc^2 |
|
|
What is commutative property and give an example. What does it only work for?
|
x + y = y + x
1 +2 = 2+1 Only works for + and * Doesn't work for: - and / |
|
|
What is associative property?
What does it only work for? |
(x+y) + z = x + (y+z) and
(xy)z = x(yz) works for + and * only. |
|
|
What is the mnemonic for remembering the order of operations?
|
PEMDAS
|
|
|
What is the Chad way you like for ADDING fractions with whole numbers? ie:
2 3/4 + 3 1/3 = |
#1) Add the whole #'s first
#2) Then add the left overs NOTE: This only works for adding fractions not multiplication or division. |
|
|
Comparing fractions. List your plan of attack
|
1) Fastest way is to compare them to 1/2 as the base line.
2) Take difference between numerator and denominator -> Bigger Difference = largest fractions -> If same Difference = the largest numerator wins 3) Narrowed down to two numbers. Cross multiply and focus on the numerator -> Biggest numerator wins. |
|
|
What does percent mean?
|
per
cent = 100 -> per 100 How many of something you have per 100 of total |
|
|
What is the percent verbage?
|
% = is/of x 100
|
|
|
What is the most effective method for solving for percents?
|
Solve for the "is"
% =is/of x 100 |
|
|
What is the percentage break down method?
What is 18% of 250 |
Break down numbers to percentages we can easily do in our head.
10% of 250 = 25 1% of 250 = 2.5 So.. 10% +10% -1% -1% = 18% 25+25-2.5-2.5 = 45 (BAMB!) |
|
|
What if we are not solving for "is" when talking about percentages?
Look at: 176 is what percentage of 22? |
1) Write down your mnemonic
% = is/of x 100 2) % = 176/22 x 100 Better to understand this in your head 1) what is 100% of 22 = 22 => so we know the number will be way over 100% 2) Give yourself some easy parameters. 10x22 = 220 5x22 = 110 So we know the answer will be between 700-800. you are done if you can find that. |
|
|
What does each of these mean?
100% 200% 300% 1000% |
100% = Full value
200% = x2 full value 300% = x3 full value 1000% = x10 full value |
|
|
Ultimately what is the best approach for solving for percentages?
176 is what percentage of 22? |
Do this in your head, by making them into nice numbers.
176/22 x 100 I decrease numerator to 20. Which creates a small amount of error. -> Decrease to numerator to minimize the error. But in this case we know that 178 is closer to 180. If you: 1) Make the numerator bigger the # is going to be a little bit high. . 2) make the denominator smaller the # is a little high. So...our approximate answer will come out a little high. So - ACTUAL answer will be a little low, but close to ours. |
|
|
Give me the percentages of:
1/2 = 1/3 = 1/4 = 1/5 = 1/6 = 1/7= 1/8 = 1/9 = 1/10 = 1/20 = 1/25 = |
1/2 = 50%
1/3 = 33.3% 1/4 = 25% 1/5 = 20% 1/6 = 12.5% 1/7= 14.2% 1/8 = 12.5% 1/9 = 11.1% 1/10 = 10% 1/20 = 5% 1/25 = 4% |
|
|
what steps would you take if you saw this problem?
$1,200 increased by 20% then decreased by 20% |
This method helps you know what side of the equation you will be on.
Since same percentage you know that the percent decrease will be greater than the percent increase. So in your answer you will be looking for something less than the starting amount. If it asked you to decrease by 20% then increase by 20% the answer will still be below the actual value |
|
|
What are each of theses squared?
1= 2 3 4 5 6 7 8 9 10 |
Left side is squared
1= 1 2 = 4 3= 9 4= 16 5= 25 6= 36 7= 49 8= 64 9= 81 10= 100 |
|
|
What does each of these mean?
100% 200% 300% 1000% |
100% = Full value
200% = x2 full value 300% = x3 full value 1000% = x10 full value |
|
|
Ultimately what is the best approach for solving for percentages?
176 is what percentage of 22? |
Do this in your head, by making them into nice numbers.
176/22 x 100 I decrease numerator to 20. Which creates a small amount of error. -> Decrease to numerator to minimize the error. But in this case we know that 178 is closer to 180. If you: 1) Make the numerator bigger the # is going to be a little bit high. . 2) make the denominator smaller the # is a little high. So...our approximate answer will come out a little high. So - ACTUAL answer will be a little low, but close to ours. |
|
|
Give me the percentages of:
1/2 = 1/3 = 1/4 = 1/5 = 1/6 = 1/7= 1/8 = 1/9 = 1/10 = 1/20 = 1/25 = |
1/2 = 50%
1/3 = 33.3% 1/4 = 25% 1/5 = 20% 1/6 = 12.5% 1/7= 14.2% 1/8 = 12.5% 1/9 = 11.1% 1/10 = 10% 1/20 = 5% 1/25 = 4% |
|
|
what steps would you take if you saw this problem?
$1,200 increased by 20% then decreased by 20% |
This method helps you know what side of the equation you will be on.
Since same percentage you know that the percent decrease will be greater than the percent increase. So in your answer you will be looking for something less than the starting amount. If it asked you to decrease by 20% then increase by 20% the answer will still be below the actual value |
|
|
What are each of theses squared?
1= 2 3 4 5 6 7 8 9 10 |
Left side is squared
1= 1 2 = 4 3= 9 4= 16 5= 25 6= 36 7= 49 8= 64 9= 81 10= 100 |
|
|
What are each of these cubed?
1 2 3 4 5 3^4 |
1 = 1
2= 8 3=27 4=64 5=125 3^4 = 81 |
|
|
Give me the formulas for finding these main reference points for the DAT
Kelvin Celsius F |
K = C + 273
C = K-273 F = 9/5C +32 Just memorize one and switch if it you need to. -40F - -40C 32 F = 0 C |
|
|
What are the main temperature reference points to help you with temperature problems?
|
0C = 273 K = 32F and
77 F, 25 C = 298K |
|
|
1 mile = ?ft
1 in = ? cm Terra = Giga = Mega = Kilo = Centi = milli = micro = nano = pico = femto = |
1 mile = ?ft
1 in = ? cm Terra = Giga = Mega = Kilo = Centi = milli = micro = nano = pico = femto = |
|
|
What is the distance formula for a 2D triangle and for 3D rectangle?
|
Pythagorean Theorem :
a^2 + b^2 = c^2 ,which is the same as d = sqr. root [x2 - x1)^2 + (y2 - y1)^2] 3D rectangle distance formula d = square root [x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2] |
|
|
Total cards in a deck:
How many suites: Cards in each suite: |
Total cards in a deck: 52
How many suites: 4 Cards in each suite: 13 |
|
|
What method should you use when dealing with age problems? Say for Joe and Bob
|
THe now and later method.
Now Later Joe ___ ____ Bob ___ ______ |
|
|
What are the two rate formulas you should know?
|
d = r * t
or d = v * t |
|
|
When dealing with train problems, what is the key regarding their rates?
|
Rates are additive.
You can add the two rates together to solve for distance/v to get time. |
|
|
WHat is the Kaplan equation for solving for work that you like?
|
(work1 * work 2)/ (work 1+ work 2)
|
|
|
Trigonometry:
What is an easy way to remember your signs in each Quadrant for Sin, Cos, Tan, and All of them? |
ACTS
A = All Trig functions are (+) sin, cos, tan in quadrant I. C = Cos is ONLY + in IV T = Tan is ONLY + in III S = Sin is ONLY + in II |
|
|
Trig:
What 1 or 2 trig function should you know to get the rest? |
1) Know either SIN or COS
2) And know their complementary angels = Know these and you can find the rest. (See table on notes) |
|
|
How do you write out 4 consecutive odd integers?
|
(2x-1) + (2x+1) + (2x+3) + ( 2x+5)
|
|
|
How to you write two consecutive integers?
|
First integer = x
Second integer = x+1 The Sum = x + (x+1) = 2x +1 |
|
|
What does consecutive mean?
|
consecutive integers are integers that follow each other in order. They have a difference of 1 between every two numbers. In a set of consecutive integers, the mean and the median are equal.
If n is an integer, then n, n+1, and n+2 will be consecutive integers. |
|

WORD PROBLEMS: What do these words mean?
|

|
|
|
What are thy pythagorean triplets you should be looking for?
|
(3,4,5)
(5,12,13) (7,24,25) (8, 15, 17) (9, 40, 41) etc |
|
|
What are the equations for a 30:60:90 and 45:45:90 triangles?
|
30:60:90 =
x : x sq.rt.3 : 2x 45 : 45 : 90 x : x : x sq.rt.2 |
|
|
How do you find the Area of a Sector?
Length of Arc? |
Area of Sector (like the are of a slice of pizza) =
(x degrees/ 360 degrees)(Area of circle) Length of Arc= (x degrees / 360 degrees)(Circumference of circle) |

