![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
15 Cards in this Set
- Front
- Back
|
Sobre os diagramas de dispersão para duas variáveis é correto afirmar que se a nuvem de pontos distribui-se nas proximidades de uma reta, então há correlação linear
|
Falso. Se a reta for horizontal, não há correlação linear.
|
|
|
Sobre os diagramas de dispersão para duas variáveis é correto afirmar que se a nuvem de pontos não se distribui nas proximidades de qualquer que seja a reta, então não há correlação.
|
Falso
|
|
|
Sobre os diagramas de dispersão para duas variáveis é correto afirmar que se todos os pontos de diagrama pertencem a uma única reta oblíqua, então há correlação linear perfeita.
|
Verdadeiro
|
|
|
Sobre os diagramas de dispersão para duas variáveis é correto afirmar que se a nuvem de pontos distribui-se nas proximidades de uma reta que represente uma função crescente, então há correlação linear positiva.
|
Verdadeiro
|
|
|
No estudo de duas variáveis, X e Y, com desvios-padrão respectivamente iguais a 2,6 e 3,1, apurou-se uma covariância igual a -7,3. Com base nestas informações, pode-se afirmar que a variável X apresenta menor dispersão que a variável Y.
|
Falso. Se X e Y forem de grandeza ou possuirem unidades de medida diferentes, o desvio-padrão sozinho não será suficiente para comparar suas dispersões (melhor utilizar o Coeficiente de Variação de Pearson)
|
|
|
No estudo de duas variáveis, X e Y, com desvios-padrão respectivamente iguais a 2,6 e 3,1, apurou-se uma covariância igual a -7,3. Com base nestas informações, pode-se afirmar que existe uma correlação linear perfeita entre X e Y.
|
Falso
|
|
|
No estudo de duas variáveis, X e Y, com desvios-padrão respectivamente iguais a 2,6 e 3,1, apurou-se uma covariância igual a -7,3. Com base nestas informações, pode-se afirmar que existe uma forte correlação negativa entre X e Y.
|
Verdadeiro
|
|
|
No estudo de duas variáveis, X e Y, com desvios-padrão respectivamente iguais a 2,6 e 3,1, apurou-se uma covariância igual a -7,3. Com base nestas informações, pode-se afirmar que nada se pode afirmar sobre a força da correlação entre X e Y.
|
Falso
|
|
|
0,989
|
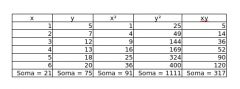
Qual o coeficiente de correlação linear (com precisão de 0,001) entre as variáveis X e Y?
|
|
|
Dado que
n = 6 sum(x) = 21 sum(y) = 75 sum(x^2) = 91 sum(y^2) = 1111 sum(xy) = 317 Calcule a reta de regressão linear simples ajustada pelo método dos mínimos quadrados. |
y = 1,6 + 3,114x + e
|
|
|
Em um estudo sobre a relação entre as variáveis tempo de serviço (em anos) e salário (em milhares de cruzeiros) dos empregados de uma empresa, foi utilizado o modelo linear simples Y = a + bx + e, onde Y é o salário do empregado, x é o tempo de serviço do empregado e "e" é o erro aleatório, com as suposições usuais. Selecionou-se ao acaso uma amostra de 100 empregados, resultando:
sum(x) = 800 var(y) = 6000 b = 0,2 Nessas condições, julgue o item abaixo: O salário de um empregado recém-contratado é de $ 50.000,00. |
FALSO
|
|
|
Em um estudo sobre a relação entre as variáveis tempo de serviço (em anos) e salário (em milhares de cruzeiros) dos empregados de uma empresa, foi utilizado o modelo linear simples Y = a + bx + e, onde Y é o salário do empregado, x é o tempo de serviço do empregado e "e" é o erro aleatório, com as suposições usuais. Selecionou-se ao acaso uma amostra de 100 empregados, resultando:
sum(x) = 800 var(y) = 6000 b = 0,2 Nessas condições, julgue o item abaixo: O salário médio de empregados com 10 anos de serviço é de $ 62.000,00 |
FALSO
|
|
|
Em um estudo sobre a relação entre as variáveis tempo de serviço (em anos) e salário (em milhares de cruzeiros) dos empregados de uma empresa, foi utilizado o modelo linear simples Y = a + bx + e, onde Y é o salário do empregado, x é o tempo de serviço do empregado e "e" é o erro aleatório, com as suposições usuais. Selecionou-se ao acaso uma amostra de 100 empregados, resultando:
sum(x) = 800 var(y) = 6000 b = 0,2 Nessas condições, julgue o item abaixo: O coeficiente de correlação entre salário e tempo de serviço é -0,3 |
FALSO
Como b é positivo, a correlação também o é. |
|
|
Em um estudo sobre a relação entre as variáveis tempo de serviço (em anos) e salário (em milhares de cruzeiros) dos empregados de uma empresa, foi utilizado o modelo linear simples Y = a + bx + e, onde Y é o salário do empregado, x é o tempo de serviço do empregado e "e" é o erro aleatório, com as suposições usuais. Selecionou-se ao acaso uma amostra de 100 empregados, resultando:
sum(x) = 800 var(y) = 6000 b = 0,2 Nessas condições, julgue o item abaixo: Tendo obtido um coeficiente de determinação igual a 10%, o modelo proposto deve ser julgado inadequado. |
VERDADEIRO
|
|
|
Em um estudo sobre a relação entre as variáveis tempo de serviço (em anos) e salário (em milhares de cruzeiros) dos empregados de uma empresa, foi utilizado o modelo linear simples Y = a + bx + e, onde Y é o salário do empregado, x é o tempo de serviço do empregado e "e" é o erro aleatório, com as suposições usuais. Selecionou-se ao acaso uma amostra de 100 empregados, resultando:
sum(x) = 800 var(y) = 6000 b = 0,2 Nessas condições, julgue o item abaixo: O grau de instrução é também um variável explicativa do salário. |
FALSO
O grau de instrução do empregado não foi contemplado no modelo Y = a + bx. |

