Statistiek Inductieve Technieken H3. Kansen En Kansverdelingen

Front 1

3. Kansen en kansverdelingen

3.1 kansbegrip

Wat is het begrip ‘kans’?

Back 1

Uitganspunt bij de precisering van het begrip ‘kans’ is de opvatting dat het kansbegrip betrekking heeft op de mogelijke, verschillende, uitkomsten van gebeurtenissen.

Praten over kansen waarvan maar 1 uitkomst zeker is, is zinloos.

Front 2

P = Propability.
De kans op bijvoorbeeld een man: P = (M)

Back 2

Het is de kans op een gebeurtenis dat we een man treffen.

Front 3

Stel we hebben een verzameling elementen (N = 50), waarvan er een aantal elementen het kenmerk M hebben (M = man) en de overige niet. (niet-M).

De kans dat we een man treffen (M is gelijk aan het aantal elementen met het kenmerk M, gedeeld door het totale aantal elementen (N).

Stel dat je 30 mannen hebt (N =30) op een totaal aantal elementen van N =50, bereken je de als kans op een man:

Back 3

P(M) = N(M)/N.
P(M) = 30/50 = 3/5

Front 4

De kans op een vrouw P (V) is nu eenvoudig te berekenen.

Want de som van de kansen zijn altijd gelijk aan 1.

Back 4

P (M) + P (V) = 1 Je trekt tenslotte altijd of een man, of een vrouw.

De Kans op een vrouw is dan ook: N=50 - P(M) = N 50 – P30 = P(V) 20.

Of N-P(M) = 1-3/5 = 2/5

Aan de berekening van P (M) = 3/5 ligt de aanname ten grondslag dat elk element uit de groep dezelfde kans heeft om getrokken te worden. Dat hoeft niet altijd het geval te zijn. Door deze veronderstelling te maken komen we meteen in een kansmodel terecht.

Front 5

Kansmodel:
Een kansmodel is een model dat

Back 5

precies aangeeft hoe we onze kansen moeten berekenen.

Voorbeeld dobbelsteen:
Ook bij een dobbelsteen is er spraken van kansen. Met zes ogen is er dan ook kans van 1/6 dat een cijfer wordt gegooid. Met andere woorden:
P (1) = 1/6
P (2) = 1/6
P (3) = 1/6
P (4) = 1/6
P (5) = 1/6
P (6) = 1/6


Bij elkaar opgeteld wordt het uiteraard 1.

Front 6

Relatieve frequentie van een gebeurtenis.

Stel dat we bijhouden hoe vaak we een 3 gooien of niet. We delen dan na elke worp het aantal malen dat tot dan toe de 3 boven is gekomen door het totale aantal worpen.

Zo krijgen we:

Back 6

de relatieve frequentie dat een worp boven is gekomen.

Dat zal schommelen in het begin, maar steeds meer naar elkaar toe trekken..

Op de lange duur blijft er de relatieve frequentie van 1/6 (=0,167) over.
Dat is de kans dat een 3 bovenkomt bij het werpen van een eerlijke dobbelsteen.

Front 7

Als de kans op een gebeurtenis klein is (in de buurt van 0 ligt), wijst dit op een gebeurtenis die zelden plaatsvindt.

Een grote kans, in de buurt van 1, zegt dat die kans vrijwel zeker plaatsvindt.

Is de kans ½, dan zijn we:

Back 7

maximaal onzeker over het optreden van de betreffende gebeurtenis.

Front 8

3.2 berekening van kansen

Uitkomstruimte
Uitkomstruimte is:

Back 8

de totaal aantal mogelijkheden op een een ‘gunstige’ uitkomst.
Bij een dobbelsteen zijn dat er 6. (1, 2, 3 ,4 ,5 en 6). Deze bij elkaar zijn dus de uitkomstruimte.

Uitkomstruimte wordt geschreven als U
Alle gebeurtenissen binnen een dobbelsteen bestaan uit deze ruimte. Ze vinden plaats binnen deze ruimte.

Front 9

Uitkomstruimte wordt geschreven als

Back 9

U

Alle gebeurtenissen binnen een dobbelsteen bestaan uit deze ruimte. Ze vinden plaats binnen deze ruimte.

Front 10

Elementaire gebeurtenissen.

Elementaire gebeurtenissen zijn de gebeurtenissen die

Back 10

slechts 1 uitkomst bevatten binnen de uitkomstruimte.

Bij een dobbelsteen zijn er dan ook 6 elementaire gebeurtenissen mogelijk.
De elementaire gebeurtenis bij een dobbelsteen is gelijk aan 1/6.

Front 11

Uniform kansmodel.

De kans op elementaire gebeurtenissen binnen een de uitkomstruimte U heet

Back 11

een kansmodel.
Omdat de kansen allemaal gelijk zijn heet het een uniformkansmodel.

Stel dat je een uniform kansmodel opstelt voor de 30 mannen en 20 vrouwen, is de uitkomstruimte:
U = (M1, M2, M3, M4….M30, V1, V2, V3… V20.
De kans op een willekeurige gebeurtenis is 1/50

Front 12

Samengestelde gebeurtenis.
Hoe groot is de kans op een samengestelde gebeurtenis?
De kans dat er 2 of meer elementaire gebeurtenissen samen plaatsvinden?

Voorbeeld:
Hoe groot is de kans P(A) dat een dobbelsteen 5 of hoger uitvalt?
Of de kans P(B) op de gebeurtenis dat we een man trekken uit een groep mannen en vrouwen?

Back 12

Elementaire gebeurtenissen sluiten elkaar uit, daar kunnen we gebruik van maken.
Als 5 bovenkomt, kan 6 niet boven liggen.

In het geval van 5 of hoger gooien is het P(A) =5 ogen boven of 6 ogen boven
Is P (5) + p(6) = 1/6 + 1/6 =2/6 = 1/3


Bij de mannen is het P (M) 30/ N50 = 30/50 = 3/5

Front 13

Opgave 3.1
Hoe groot is de kans op een 3 of een 5 als we een keer met een dobbelsteen gooien?

Back 13

Antw.
De gebeurtenis dat een dobbelsteen met een 3 bovenkomt, noemen we even X=3 en de gebeurtenis dat een 5 bovenkomt Y=5. De gebeurtenissen sluiten elkaar uit, dus de gevraagde kans is:
P (X=3 of Y=5) = P (X=3) + P (Y=5) = 1/6 + 1/6 = 2/6 =1/3.

Volgens de kans definitie: het aantal elementaire gebeurtenissen in ‘X of Y’ is 2 en in U is het 6, dus de kans is 2/6 (=1/3).

Front 14

Opgave 3.2
Hoe groot is de kans dat ik één, twee, drie, vier, vijf of zes ogen gooi met een dobbelsteen?

.

Back 14

Antwoord
In feite vragen we dus de kans P (U). Welnu, we weten zeker dat we een van de genoemde aantallen ogen gooien, dus de kans P (U) = 6/6 = 1. Uiteraard hadden we ook de kansen op alle samenstellende elementaire gebeurtenissen kunnen optellen. We hadden dan 6 x 1/6 = 1 gekregen.

Front 15

Opgave 3.3
Hoe groot is bij een normale dobbelsteen de kans op de gebeurtenis 'een 7 komt boven'?

Back 15

Antwoord
De gebeurtenis 'een 7 komt boven' is onmogelijk binnen de uitkomstenruimte van de dobbelsteen en zal dus ook niet plaatsvinden: de kans op een onmogelijke gebeurtenis is 0.

Front 16

Opgave 3.4
Hoe groot is de kans op een man of een vrouw bij de trekking van een persoon uit een groep van vijftig personen die bestaat uit dertig mannen en twintig vrouwen?

Back 16

Antwoord
De kans op een man hebben we al uitgerekend, die was 3/5. Voor de kans op een vrouw geldt volgens de zojuist geïntroduceerde definitie P (V) = 20/50 = 2/ 5.

Beide gebeurtenissen sluiten elkaar uit, dus we mogen de kansen optellen. De kans op of man of vrouw is 3/5 + 2/5 = 1

Front 17

Waaraan moeten kansen binnen een willekeurige uitkomstruimte U voldoen?

Back 17

1. Voor de kans op een gebeurtenis A geldt P (A) ≥ 0
2. P (U) = 1
3. Als twee gebeurtenissen A en B elkaar uitsluiten geldt P (A of B) = P (A) + (B).

Je krijgt dan ook:

0 ≤ P ≤ 1

De kans is 0 als de gebeurtenis onmogelijk is.
De kans is 1 als de gebeurtenis zeker plaatsvindt

Front 18

Complementaire gebeurtenis.
Er is een gebeurtenis die altijd plaatsvindt, namelijk de gebeurtenis A of Niet-A. Daarin is Niet-A de

Back 18

complementaire gebeurtenis.
Of geen man
Of niet 5

De gebeurtenissen sluiten elkaar dus uit.
Het gevolg is dat P(A of Niet-A) = P(A) + P(Niet-A)

P(Niet-A) is 1-P(A)
Denk aan de dobbelsteen:
P (Niet-A) = 1 – 1/6 = 5/6

Als we P(Niet-A) kennen, kan je dus P(A) berekenen omdat:
P(A) = 1 – P(Niet-A) = 1/6
P(A) = 1 – 5/6 = 1/6

Front 19

3.2.1 De kans op A of B
De kans op A of B heten ook wel de somregel van elkaar uitsluitende gebeurtenissen.
Deze geldt voor als A of B plaatsvindt, maar niet tegelijk.



Somregel: elkaar uitsluitende gebeurtenissen
P (A of B) = P(A) + P(B)
A en B sluiten elkaar uit.

De somregel geldt lang niet altijd.. Bijvoorbeeld als er 2 of meer gegooid wordt, of 4 of minder.
Dan sluiten de gebeurtenissen elkaar niet uit, want ze hebben uitkomsten gemeen. Namelijk de uitkomsten 2, 3 en 4. De kans op A of B moet 1 zijn, maar als we dit doen: A(5/6) + B(4/6) = 9/6 = 1,5
Dat kan niet.

Back 19

De somregel bij elkaar niet uitsluitende gebeurtenissen is dan ook anders:
Je zou dingen dubbel tellen.

Stel dat de som is
P (A of B) = P (A) + P (B) = A(5/6) + B(4/6) = 9/6 = 1,5 dan is dat onmogelijk

Dus is het
P (A of B) = P (A) = P (B) – P (A en B)
A(5/6) + B(4/6) = 9/6 – 3/6 = 6/6 = 1

Front 20

Opgave 3.5
In een groep van 1000 mensen roken 400 mensen sigatetten (A) en 200 roken er sigaren (B). Van de rokers roken er 100 zowel sigaren als cigaretten..
Als we Aselect iemand uit de 1000 mensen terkken, hoe groot is dan de kans op iemand die rookt?

Back 20

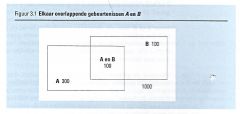
Antwoord:
P(A) = (300+100)/1000 = 400/1000 =0,4
P(B) = (100+100)/1000 = 200/1000 =0,2

P (A en B) = 100/1000 = 0,1

P(A of B) = P(A) + P(B) – P(A en B) = 0,4 + 0,2 – 0,1 = 0,5

Front 21

3.2.2 De kans op A en B

We hebben het tot nu toe gehad over 'of -gebeurtenissen. We wilden bijvoorbeeld de kans weten op een 5 of een 6 als we één keer met een dobbelsteen gooiden. Nu gaan we ons bezighouden met 'en-en'-gebeurtenissen;

situaties dus waarin twee gebeurtenissen tegelijkertijd optreden. We beginnen met een voorbeeld waarin iemand één keer gooit met twee geldstukken A en B. Hoe groot is de kans dat deze met geldstuk A
'munt' gooit en met geldstuk B 'kop'?

Back 21

We noteren de uitkomst kop als K en de uitkomst munt als M. De uitkomstenruimte bestaat uit vier mogelijke gebeurtenissen die allemaal even waarschijnlijk zijn:

Front 22

Een van de vier mogelijke gebeurtenissen is de gevraagde, dus de kans die we moeten hebben is 1/4.

Ook deze opgave kunnen we iets anders oplossen als we gebruikmaken van het feit dat het optreden van de gebeurtenis A = M niets zegt over de kans op de gebeurtenis B = K. De gebeurtenissen zijn dan onafhankelijk en we mogen dan de kansen op het optreden van beide vermenigvuldigen, zodat:

Back 22

P (A = M én B = K) = P (A = M) · P (B = K) = 1/2 x 1/2 = ¼

Om uit te leggen waarom dit mag, moeten we eerst het begrip 'voorwaardelijke kans' introduceren. We bedoelen daarmee de kans dat gebeurtenis A zal gaan plaatsvinden als al bekend is dat gebeurtenis B
heeft plaatsgevonden.

Front 23

Als A en B gebeurtenissen zijn, is

Back 23

P (A/B) de voorwaardelijke kans op A wanneer B heeft plaatsgevonden.

De voorwaardelijke kans P (A/B) lezen we hierbij als 'de kans op A gegeven dat B heeft plaatsgevonden' of kortweg 'de kans op A gegeven B;

de streep staat dus voor 'gegeven dat' of 'gegeven'. Zo bestaat ook P (A/B), hetgeen men moet lezen als 'de kans op E gegeven A'. Inhoudelijk betekent de voorwaardelijke kans P (A/B) dat we slechts de kans op de gebeurtenis A bezien onder de voorwaarde dat gebeurtenis B zich heeft voorgedaan. We bevinden ons binnen de gebeurtenis B en bepalen daarbinnen de kans op gebeurtenis A.

Front 24

de streep staat dus voor 'gegeven dat' of 'gegeven'. Zo bestaat ook P (A/B), hetgeen men moet lezen als 'de kans op B gegeven A'.

Inhoudelijk betekent de voorwaardelijke kans P (A/B) dat we slechts de kans op de gebeurtenis A bezien onder de voorwaarde dat

Back 24

gebeurtenis B zich heeft voorgedaan. We bevinden ons binnen de gebeurtenis B en bepalen daarbinnen de kans op gebeurtenis A.

Front 25

Opgave 3.6
Veronderstel dat iemand gooit met een dobbelsteen en zegt dat zij hoger dan 2 heeft gegooid. Hoe groot is dan de kans dat zij een 6 heeft gegooid?

Back 25

Antwoord
Hiermee wordt een vraag gesteld naar de voorwaardelijke kans P (A/B). De gebeurtenis B is in dit geval dat 3, 4, 5 of 6 is gegooid (vier mogelijke uitkomsten dus). De gebeurtenis A is dat een 6 bovenkomt (één gunstige uitkomst). De voorwaardelijke kans is daarom P (A/B) = 1/4.

Front 26

We kijken bij de vraag P (A/E) binnen de gebeurtenissen B of de gebeurtenis A plaatsvindt. Merk op dat in opgave 3.6 de kans op A (dus zonder voorkennis) 1/6 is.

Back 26

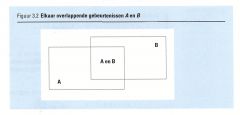
Weet hebben van voorwaarden beïnvloedt oe kansen als de gebeurtenissen iets met elkaar hebben uit te staan. Als we ons bij de voorwaardelijk kans P (A/B) binnen de gebeurtenis B bevinden en daarin naar de kans op A vragen, dan maakt figuur 3.2 duidelijk dat we in feite vragen naar de kans op 'A en B' binnen B.

Front 27

In formule vorm:

Back 27

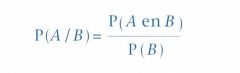
Voorwaardelijke kans

Front 28

Bij de voorwaardelijke kans P (A/B) in opgave 3.6 is B gelijk aan 'hoger dan 2' en is A gelijk aan 6, dus P (A en B) = 1/6.

Nu geldt:
P (B) = 4/6 en P (A en B) =1/6 (want als A zich voordoet, doet B zich ook voor) .
Dus de kans op A gegeven B wordt:

Back 28

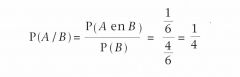
de kans op A gegeven B



We zien dus dat P (A/B) niet gelijk is aan P (A). De kans op A gegeven B kan dus verschillend zijn van de kans op A zonder meer.

Front 29

Voorbeeld 3.1

Veronderstel dat A is 'een verkeersongeluk krijgen', en B is 'roekeloos rijden', zodat A en B iets met elkaar te maken hebben. We verwachten daarom nu dat P (A) (de kans op een verkeersongeluk) anders is dan P (A/B) (de kans op een verkeersongeluk, gegeven dat we weten dat de bestuurder roekeloos rijdt), omdat roekeloos rijden een oorzaak is van verkeersongelukken en er dus een relatie is tussen A en B.


Wat gebeurt er nu als A en B niets met elkaar hebben uit te staan, als de kans op het optreden van gebeurtenis A in geen enkel opzicht afhankelijk is van het optreden van gebeurtenis B?

Back 29

We zeggen dan dat de gebeurtenissen A en B onafhankelijk zijn van elkaar.

Omdat het in dit geval niets uitmaakt of B wel of niet heeft plaatsgevonden, is de voorwaardelijke kans op A gegeven B (dus P (A/B)) precies even groot als de kans op A zonder dat we iets weten over B.

Gebeurtenis B oefent immers geen enkele invloed uit op de kans dat gebeurtenis A gaat plaatsvinden.

Front 30

Omdat het in dit geval niets uitmaakt of B wel of niet heeft plaatsgevonden, is de voorwaardelijke kans op A gegeven B (dus P (A/B)) precies even groot als de kans op A zonder dat we iets weten over B. Gebeurtenis B oefent immers geen enkele invloed uit op de kans dat gebeurtenis A gaat plaatsvinden.

We definiëren het begrip 'onafhankelijkheid' daarom als volgt:

Back 30

P (A/B) = P (A)

Front 31

Dus de kans dat A plaatsvindt blijft hetzelfde en is onafhankelijk van het feit of B wél of niet heeft plaatsgevonden en vice versa. Als A en B onafhankelijk zijn, helpt kennis omtrent de één niet bij het voorspellen van de ander.

De formule voor de voorwaardelijke kans op A gegeven B is gelijk aan:

Back 31

Front 32

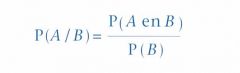
Als A en B onafhankelijk zijn, geldt P (A/B) = P (A) . Wanneer we daarom P (A) invullen in het linkerlid van de formule hiervóór, krijgen we:

Back 32

Front 33

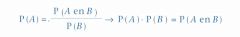
We kunnen onafhankelijkheid dus ook als volgt definiëren:

Definitie 2 onafhankelijkheid

Back 33

Als P (A) · P (B) = P (A en B)

Front 34

Beide definities zijn volstrekt gelijkwaardig, en we komen ze allebei dan ook nog vaak tegen.


Definitie 1
Definitie 2

Back 34

Definitie 1
P (A/B) = P (A)

geeft het duidelijkst aan dat onafhankelijkheid inderdaad betekent dat de gebeurtenissen niets met elkaar hebben uit te staan.

Definitie 2
Als P (A) · P (B) = P (A en B)

laat zien dat twee gebeurtenissen A en B onafhankelijk zijn van elkaar als de kans op de gebeurtenissen samen, P (A en B) dus, gelijk is aan het product van de afzonderlijke kansen op A en B.

We mogen definitie 2 ook omdraaien tot de zogenaamde productregel voor onafhankelijke gebeurtenissen.

Front 35

Productregel voor onafhankelijke gebeurtenissen
P (A en B) = P (A) · P (B)

Back 35

Front 36

Deze regel stelt ons in staat om de kans op A en B te berekenen als de twee gebeurtenissen onafhankelijk zijn.

Dat A en B hierin onafhankelijk zijn, betekent nogmaals dat de uitkomst van de één niet de kans op
de uitkomst van de ander mag beïnvloeden.

Gebruikmakend van deze regel kunnen we de kans uitrekenen waarmee

Back 36

we de bespreking van de kans op 'A en B' begonnen. Daarbij wierp iemand éénmaal met twee geldstukken A en B en vroegen we hoe groot de kans was dat bij geldstuk A 'munt' boven zou komen en bij geldstuk B 'kop'.

Front 37

Omdat het optreden van de gebeurtenis A = M (munt) niets zegt over de kans op de gebeurtenis B = K (kop) zijn beide gebeurtenissen onafhankelijk.

Dus moeten we de kansen op het optreden van beide vermenigvuldigen, zodat:

Back 37

Front 38

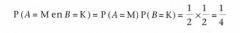
Opgave 3.7

Ik gooi één keer met twee dobbelstenen A en B. Hoe groot is de kans dat ik met dobbelsteen A een 2 gooi en met dobbelsteen B een 4?

Back 38

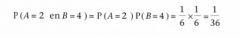
Antwoord
Beide gebeurtenissen zijn onafhankelijk van elkaar, dus:

Front 39

We kunnen dit ook illustreren aan de hand van figuur 3.3, die dit resultaat laat zien via de uitkomstenruimte met een uniform kansmodel.

We kunnen dit ook illustreren aan de hand van figuur 3.3, die dit resultaat laat zien via de uitkomstenruimte met een uniform kansmodel.

Back 39

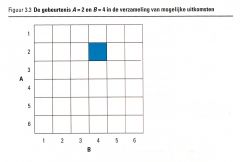
Er zijn 36 mogelijke gebeurtenissen die allemaal even waarschijnlijk zijn.

Eén van deze gebeurtenissen is de gebeurtenis 'A = 2 en B = 4', dus is de gevraagde kans:

P (A = 2 en B = 4) = 1/36 .

Front 40

Algemene productregel

Wanneer A en B onafhankelijk zijn, geldt een meer algemene productregel voor 'en-en'-gebeurtenissen. Deze volgt rechtstreeks uit de definitie van de voorwaardelijke kans P (A/B) (of P (B/A )) .

Algemene productregel:

Back 40

Algemene productregel
P (A en B) = P (A) · P (B/A)

Of

P (A en B) = P (B) · P (A/B)

waarbij A en B afhankelijk mogen zijn .

Front 41

Algemene productregel
P (A en B) = P (A) · P (B/A)

Of

P (A en B) = P (B) · P (A/ B)

waarbij A en 8 afhankelijk mogen zijn .

Deze regel geeft de kans dat

Back 41

twee gebeurtenissen zich samen voordoen, ongeacht of de gebeurtenissen afhankelijk dan wel onafhankelijk zijn.

Dat de regel ook voor onafhankelijke gebeurtenissen werkt, is overigens gemakkelijk in te zien door voor P (A/B) de kans P (A) in te vullen of voor P (B/A) de kans P (B). We krijgen dan P (A en B) = P (A) · P (B) en dit is de productregel voor onafhankelijke gebeurtenissen die we eerder tegenkwamen.

Front 42

• Voorbeeld 3.2
Veronderstel dat we in een onderzoek de beschikking hebben over een populatie met de volgende (hypothetische) gegevens.

Als we aselect een persoon uit deze populatie trekken, hoe groot is dan de kans dat het een agressief roodharig iemand is?

Back 42

Merk, voordat we aan de oplossing beginnen, allereerst op dat het om een 'en-en' -gebeurtenis gaat, ook al komt het woord 'én' niet in de vraag voor.

Het gaat immers om de kans dat iemand én roodharig is én agressief. Aangezien er op een totaal van 2000 personen 300 agressieve roodharigen zijn, is de
gevraagde kans gelijk aan 300/2000 = 0, 15.

Dezelfde kans kunnen we ook berekenen door de algemene productregel toe te passen.

Front 43

Dezelfde kans kunnen we ook berekenen door de algemene productregel toe te passen.

Veronderstel: A is de gebeurtenis dat we een roodharig iemand trekken en 8 is de gebeurtenis dat we een agressief iemand trekken.

Nu is :

Back 43

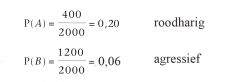
Van de 1200 agressieve personen zijn er 300 met rood haar.

Als ons verteld wordt dat de getrokken persoon agressief is, dan is de kans dat deze roodharig
is gelijk aan 300/1200 = 0,25, dus P (A/B) = 0,25.

Van de 400 roodharige personen zijn er 300 agressief. Als ons verteld wordt dat de getrokken persoon rood haar heeft, dan is de kans dat het een agressief
iemand is gelijk aan

300/400 = 0,75, dus P (B/A) = 0,75.

Front 44

We hebben nu:

P (A) =
p (B) =
P (A/B) =
P (B/A) =

Back 44

We hebben nu:

P (A) = 0,20
p (B) = 0,60
P (A/B) = 0,25
P (B/A) = 0,75

We zien inderdaad dat A en B hier niet onafhankelijk zijn van elkaar, want P (A) is ongelijk aan P (A/ B) en P (B) is ongelijk aan P (B/ A) .

Front 45

We zien inderdaad dat A en B hier niet onafhankelijk zijn van elkaar, want P (A) is ongelijk aan P (A/ B) en P (B) is ongelijk aan P (B/ A) .

Dus moeten we de algemene productregel toepassen en dan krijgen we voor de kans op een agressief roodharig iemand:

Back 45

P (A en B) = P (A)· P (B/ A) = 0,20 x 0,75 = 0,15

of

P (A en B) = P (B) · P (A/ B) = 0,60 x 0,25 = 0,15

Merk op dat dit ongelijk is aan het product P (A) · P (B) ( = 0,20 x 0,60 = 0, 12), omdat er geen sprake is van onafhankelijkheid .

Front 46

Intuïtie en voorwaardelijke kansen

De alledaagse intuïtie is niet erg nauwkeurig wanneer het om kansen gaat. Dat moge blijken uit de volgende twee voorbeelden.

Het eerste voorbeeld heeft betrekking op het 'noemen van willekeurige getallen' . Wanneer ons
wordt gevraagd om honderd keer een getal tussen de 1 en 10 te noemen, en we gaan vervolgens de genoemde getallen nauwkeurig bekijken, dan zal meestal blijken dat

Back 46

deze helemaal niet willekeurig worden gekozen. (In de statistiek heten willekeurig gekozen getallen aselecte getallen .) Getallen als 5 en 7 komen te veel voor en 1 en 9 te weinig. Daarom wordt voor het produceren van aselecte getallen meestal een tabel met aselecte getallen of een computerprogramma gebruikt.

Front 47

Het tweede voorbeeld heeft betrekking op de onnauwkeurigheid van de intuïtie wanneer het gaat
om het combineren van kansen. Een voorbeeld is het testen op hiv (a idsbesmetting) .

Veronderstel, we hebben de volgende twee gebeurtenissen:
A = het trekken van een besmet persoon
B = het vinden van een positieve tes tuitslag

Veronderstel, we hebben een test die, wanneer iemand besmet is, met een kans van 0,95 een pos itieve uitkomst geeft.
Dus:

P (B/A ) = 0,95
Wanneer iemand niet besmet is, is er slechts 0,01 kans dat de test positief uitvalt.

Dus:
P (B/ niet-A) = 0,01
We kiezen nu aselect een persoon uit de Nederlandse populatie van mensen van 18 jaar of ouder.

We nemen de test af en het resultaat is positief. Hoe groot is nu de kans dat deze persoon inderdaad
besmet is, of: hoe groot is P (A/B)?

Back 47

Intuïtief is men wellicht geneigd om te denken dat die kans 0,95 is, ofwel 95%, zoals men in het
dagelijks taalgebruik zegt.

We vragen echter om P (A/B) en niet om P (B/A).

Front 48

Veronderstel dat het percentage met hiv besmette mensen 0,01% is ofwel 0,0001.

We hebben nu:

Back 48

P (A) = 0,0001
P (niet-A) = 0,9999
P (B/A) = 0,9500
P (B/ niet-A) = 0,0100

Front 49

We kunnen nu met behulp van de algemene productregel de kansen op (A en B) en op (niet-A en
B) berekenen:

Back 49

P (A en B)
= P (A) · P (B/A)
= 0,0001 x 0,9500 = 0,000095

P (A/niet-B)
= P (niet-A) · P (B / niet-A)
= 0,9999 x 0,0100 = 0,009999

De kans op het vinden van een positieve uitslag bij een aselect getrokken persoon is P (B) en er geldt in het algemeen:

P (B) = P (A en B) + P (niet -A en B)
= 0,000095 + 0,009999 = 0,010094

Front 50

Gevraagd werd de kans op een besmetting gegeven een positieve uitslag, dus op P(A/B). Deze kans is gelijk aan:

Back 50

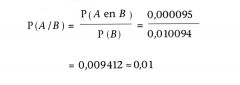
De gevraagde kans is dus gelijk aan 0,01 ofwel 1% en niet gelijk aan 95% zoals sommigen intuïtief geneigd zijn te denken.

Overigens, de kans op géén besmetting bij een positieve testuitslag is 0,990588 ofwel 99%!

In dit voorbeeld zou bij alle positieve testuitslagen tezamen in 99% van de gevallen iemand voor niets
de stuipen op het lijf zijn gejaagd.

Om deze redden is het bij zeldzame ziekten niet zinvol om de gehele Nederlandse populatie te screenen, maar wordt het onderzoek beperkt tot risicogroepen.

Front 51

3.3 Kansverdelingen

In paragraaf 3.2 hebben we terloops gebruikgemaakt van variabelen zonder daar expliciet te vermelden dat het om variabelen ging. Dat was ook niet nodig: uit de context bleek duidelijk wat de bedoeling was.

In deze paragraaf gaan we het expliciet hebben over waarden van variabelen en kansen op die waarden.

Tezamen vormen deze namelijk

Back 51

een kansverdeling.

Om duidelijk te maken wat een kansverdeling is, keren we terug naar de eerlijke dobbelsteen, want daarmee is het begrip kansverdeling het gemakkelijkst uit te leggen. Bij de dobbelsteen bestudeerden we gebeurtenissen waarbij een bepaald aantal ogen bovenkwam, met de kansen daarop. 'Vier ogen boven' was zo'n gebeurtenis en de kans daarop was 1/6.

Front 52

Als we naar het aantal ogen dat bovenkomt kijken, kunnen we daar zonder moeite een variabele van maken.

Alle waarden sluiten

Back 52

elkaar immers uit (als je een 4 gooit, gooi je geen 6) en de waarden 1 tot en met 6 zijn uitputtend (er zijn geen andere waarden mogelijk dan deze zes) .

Noemen we het aantal ogen dat bovenkomt X, dan is X dus een variabele met als mogelijke waarden de getallen 1 tot en met 6.

Front 53

Omdat X zijn waarden aanneemt met bepaalde kansen (de kans op waarde 1 van X is 1/6, enzovoort) heet X een kansvariabele (toevalsvariabele, stochastische variabele, of in het Engels: 'random variable'). Van de mogelijke waarden van X en de kansen daarop kunnen we een tabel maken (tabel3.1). Zo'n tabel heet een 'kansverdeling'.

Back 53

Front 54

Een kansverdeling is dus een tabel die alle mogelijke waarden van een variabele bevat plus de kansen op die waarden. Wil zo'n tabel een kans tot 1 verdeling zijn dan moeten alle kansen samen 1 zijn, anders is er iets
mis. In tabel 3.3 is de som inderdaad 1.

Als we zo'n tabel hebben, kunnen we er vaak snel allerlei mogelijke kansen uit afleiden. Bijvoorbeeld de kans dat X groter of gelijk is aan 3, P (X≥3). Dit is niets anders dan de som der kansen behorend bij 3 tot en met 6. Dus P (X≥3) = 4/6. Zo is ook gemakkelijk te zien dat P (X ≤ 2) = 2/6. De kans P (X≤6) is uiteraard gelijk aan

Back 54

1.

Front 55

De tabelvorm is echter niet altijd de gemakkelijkste vorm om een kansverdeling weer te geven. Zeker niet als we voor elke andere situatie weer een nieuwe (soms lange) tabel moeten maken.

We geven dan de voorkeur aan een formule die compact bij elke waarde van de toevalsvariabele de kansen geeft.

Voor de dobbelsteen zou die formule zijn:

Back 55

Voor de dobbelsteen zou die formule zijn:

Front 56

Deze formule bevat exact dezelfde informatie als de tabel. Er staat dat de kans dat X de waarde i aanneemt 1/6 is voor elke i lopend van 1 tot en met 6. In dit eenvoudige voorbeeld is deze wijze van formuleren nodeloos ingewikkeld, de tabel is veel eenvoudiger.

Maar in hoofdstuk 4 zal blijken dat op deze wijze tamelijk ingewikkelde kansverdelingen
zeer compact kunnen worden weergegeven .

Bij het één keer werpen van een dobbelsteen is de kansverdeling zo eenvoudig, omdat elke uitkomst van de steen overeenkomt met één waarde van de variabele. Maar omdat dat niet altijd het geval hoeft te zijn nemen we een iets gecompliceerder voorbeeld. In paragraaf 3.2 gooiden we op een bepaald moment met twee munten.

Laten we, met wat we nu weten, eens proberen of we de kansverdeling van het aantal malen 'kop ' kunnen opstellen voor deze situatie.

Back 56

Het aantal malen 'kop' is hier dus de kansvariabele en om hem niet te verwarren met voorgaande variabele X noemen we hem Y. Om de mogelijke waarden van Y en de bijbehorende kansen te bepalen gebruiken we (nu nog) het schema in table 3.4.

Front 57

Uit het schema lezen we zonder moeite af dat de mogelijke warden van Y gelijk zijn aan 0, 1, of 2 (dus nul maal 'kop', eenmaal ' kop', of tweemaal 'kop').

In de tabel valt op dat de waarde Y = 1 tot stand kan komen door twee mogelijke gebeurtenissen. De gebeurtenis KM leidt tot Y = 1 maar de gebeurtenis MK leidt óók tot Y = 1 en bovendien sluiten KM en MK elkaar uit.

De kans op Y = 1 is met andere woorden gelijk aan de kans dat de gebeurtenis KM optreedt plus de kans dat de gebeurtenis MK optreedt, dus: P (Y = 1) = P (KM) + P (MK) = 1/4 + 1/4 = 1/2.

Nu we dit eenmaal weten is het opstellen van de kansverdeling niet meer moeilijk. We kennen alle mogelijke waarden van Y en de kansen daarop:

Back 57

Zoals een kansverdeling betaamt, zijn de kansen in deze kansverdeling van Y samen weer precies 1.

Ook van deze kansverdeling kunnen we een formulevorm geven, maar dat stellen we uit tot de binomiale verdeling in hoofdstuk 4.

Front 58

3.4 Verwachte waarde en standaardafwijking van een kansverdeling

De kansverdeling lijkt in sterke mate op

Back 58

de frequentieverdeling die in deel 1 is behandeld. Zo sterk zelfs dat we ons afvragen of er ook centrummaten en spreidingsmaten voor kansverdelingen bestaan. Maar er is een belangrijk verschil. De frequentieverdeling is gebaseerd op daadwerkelijke waarnemingellëntie-kansverdeling op theorie.

Front 59

Welke dobbelsteen of munt we ook nemen, steeds zullen de berekende kansen iets afwijken van de kansen die we in het kansmodel veronderstellen.

Gelukkig echter zijn de afwijkingen meestal zo klein dat we het model zonder meer kunnen gebruiken om uitspraken te doen over een echte dobbelsteen of munt, maar theorie blijft theorie.

Dit verschil met (werkelijke) frequentieverdelingen werkt uiteraard ook door in centrummaten zoals het gemiddelde en spreidingsmaten zoals de standaardafwijking.

Eigenlijk bestaan het gemiddelde en de standaardafwijking (zoals we die tot nu toe voor frequentieverdelingen kennen) voor kansverdelingen

Back 59

niet.

Want voor de berekening van een gemiddelde of een standaardafwijking hebben we echte waarnemingen nodig die we bij elkaar moeten kunnen optellen en wat dies meer zij, en daarover beschikken we met een kansverdeling niet.

Front 60

Om toch zoiets als een gemiddelde en een standaardafwijking te bepalen, gaan we daarom iets anders te werk.

We doen een gedachte-experiment waarin we ons voorstellen dat we oneindig vaak dezelfde dobbelsteen (of twee munten) werpen en daarbij steeds noteren wat de uitkomst is. Bij de dobbelsteen krijgen we dus steeds 1, 2, 3, 4, 5 of 6 en bij twee munten het aantal malen 'kop'.

Omdat we oneindig vaak gooien is het principieel onmogelijk om het gemiddelde en de standaardafwijking te bepalen; hoe lang we ook gooien, we raken nooit uitgegooid.

Niettemin kunnen we bij de eerlijke dobbelsteen en de twee munten nauwkeurig aangeven waarop dit gemiddelde (of de standaardafwijking) op de lange duur zou neerkomen.

Omdat dit gemiddelde echter geen empirisch gemiddelde is, geven we het vaak een aparte naam en spreken van:

Back 60

Omdat dit gemiddelde echter geen empirisch gemiddelde is, geven we het vaak een aparte naam en spreken van 'verwachte waarde':

de waarde die we op de lange duur verwachten.

(Andere benamingen die we tegenkomen voor dit begrip zijn: 'verwachting' of 'verwachtingswaarde' en in het Engels 'expected value' of 'expectation'.)

Front 61

Wanneer uit de context duidelijk is, dat het over een verwachte waarde gaat en niet over een steekproefgemiddelde, gebruiken we echter toch vaak de term gemiddelde.

Dit doen we met name wanneer ...

Back 61

het om de verwachte waarde van een populatie gaat.

We spreken dan van een populatiegemiddelde. Hoewel voor de standaardafwijking hetzelfde verhaal geldt, nemen we hier gewoon dezelfde term, zij het dat we een ander symbool gebruiken (de Griekse letter σ) om het verschil met de steekproefstandaardafwijking s aan te duiden.

Front 62

3.4 .1 Verwachte waarde

Als we bij oneindig veel observaties een gok zouden willen wagen over de waarde van het 'gemiddelde' van deze 'observaties', zouden we bij de dobbelsteen allereerst constateren dat de waarde 1 in ongeveer 1/6 van de gevallen zou voorkomen, de waarde 2 evenzo, enzovoort tot en met de waarde 6.

Noemen we E (X) de verwachte waarde van X, (waarbij de E van 'expectation' komt), dan wordt de verwachte waarde van X:

Back 62

Front 63

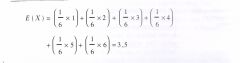
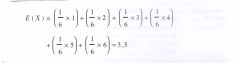
In deze formule staat steeds de kans op een specifieke waarde vermenigvuldigd met de waarde zelf, en dat opgeteld.

Het gemiddelde op de lange duur is dus 3,5 .

Veronderstel we gooien tien keer met een dobbelsteen en we berekenen het gemiddeld aantal ogen. Dat zou bijvoorbeeld 4,2 kunnen zijn. We gaan door tot we duizend keer gegooid hebben en we berekenen opnieuw het gemiddeld aantal ogen.

Wat we dan verwachten is dat het gemiddeld aantal ogen na duizend keer gooien dichter bij

Back 63

de verwachte waarde 3,5 zal liggen dan het gemiddelde na tien keer gooien.

Front 64

We geven de verwachte waarde van een kansvariabele ook vaak aan met de Griekse letter

Back 64

μ (spreek uit mu), eventueel voorzien van een verwijzing
naar de variabele μx. Dus E (X) = μx

Front 65

Zoals gezegd worden E (X) en μ ook wel .... genoemd

Back 65

het gemiddelde van de kansverdeling genoemd.

Als we de puntjes op de i zetten, is dat niet helemaal correct, want omdat het gaat om een theoretische verdeling kunnen we dit gemiddelde niet echt berekenen. Voor de interpretatie is het wel handig om te weten dat een verwachte waarde overeenkomsten vertoont met het gewone gemiddelde.

Front 66

Om de verwachte waarde E (Y) van het aantal malen 'kop' bij twee munten te bepalen, dienen we ons te realiseren dat de waarde 0 in ¼ van de gevallen zal voorkomen volgens de kansverdeling, de waarde 1 in 2/4 van de gevallen en de waarde 2 in 1/4 van de gevallen.

De verwachte waarde E (Y) wordt dus:

Back 66

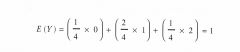
De verwachte waarde van het aantal malen kop is gelijk aan 1, ofwel het gemiddelde van een reeks worpen zal op de lange duur gelijk worden aan 1.

Front 67

Voor een willekeurige kansvariabele X met k mogelijke waarden (x 1, x2, x3, ... , xk) en bekende kansen P (X = x;) op die waarden, is de verwachte waarde:

Back 67

Dit is de algemene definitieformule van de verwachte waarde voor een willekeurige kansverdeling.

Het is gemakkelijk in te zien dat de verwachte waarde voor X en voor Y verkregen zijn door de waarden en de kansen daarop in te vullen in deze formule.

Front 68

Dit is de algemene definitieformule van de verwachte waarde voor een willekeurige kansverdeling.

Het is gemakkelijk in te zien dat

Back 68

de verwachte waarde voor X en voor Y verkregen zijn door de waarden en de kansen daarop in te vullen in deze formule.

Front 69

3.4.2 Standaardafwijking

Willen we de standaardafwijking van een kansverdeling bepalen, dan vragen we in feite naar de verwachte spreiding op de lange duur. Het gaat ook hier om een verwachte waarde, maar nu voor de spreiding rond het gemiddelde van de kansverdeling μ.

In navolging van de variantiebepaling bij de steekproef nemen we voor deze spreiding de waarden van X minus de verwachte waarde μx en dat in het kwadraat:

Back 69

dus (X- μx)2.

Front 70

De verwachte waarde van deze spreiding noemen we de variantie σ2x van de kansverdeling.

De variantie van een kansverdeling is met andere woorden:

Back 70

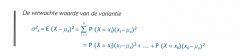
De variantie van de kansverdeling wordt dus berekend door de gekwadrateerde afwijkingen en de kansen daarop in te vullen in de formule.

Front 71

Als we hieruit de wortel trekken krijgen we de standaardafwijking van de kansverdeling σx:

Back 71

Front 72

Berekenen we de variantie voor de dobbelsteen (met μx =3,5): dan wordt deze:

Back 72

Front 73

Voor het aantal malen 'kop'(= Y) bij twee munten (met μy = 1 is de variantie:

Back 73

Front 74

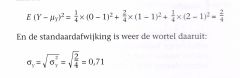
Samenvatting
Een kansmodel is een model dat aangeeft hoe we onze kansen moeten berekenen.

Een kansmodel bestaat uit

Back 74

een uitkomstellntimte (U),
elementaire gebeurtenissen, en
de kansen op die gebeurtenissen.

Wanneer de kansen op de elementaire gebeurtenissen gelijk zijn, spreken we van een uniform kansmodel.

Front 75

Wanneer A een deelverzameling is van U, is de kans op gebeurtenis A gelijk aan:
G/M (= 'gunstige' uitkomsten en 'alle mogelijke' uitkomsten).

Voor de kans op een willekeurige gebeurtenis geldt:

Back 75

0 ≤ P ≤ 1.

Front 76

Wanneer A en B elkaar uitsluiten, geldt de somregel:

Back 76

P (A of B) = P (A) + P (B).

Front 77

Wanneer A en B elkaar niet uitsluiten, geldt de algemene som regel:

Back 77

P (A of B) = P (A) + P (B) - P (A en B).

Front 78

Twee gebeurtenissen zijn onafhankelijk wanneer geldt:

Back 78

P (A/B) = P (A), dus wanneer geldt: P (A en B) = P (A) · P (B).

Front 79

Altijd geldt:

Back 79

P (A en B) = P (A)· P (B/A) of: P (A en B) = P (A /B) · P (B)

Front 80

Een kansverdeling bestaat uit alle mogelijke waarden van een variabele en de kansen op die waarden. Het 'gemiddelde' van een kansverdeling is geen empirisch gemiddelde en heet daarom de verwachte waarde.

De verwachte waarde is gelijk aan:

Back 80

Front 81

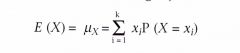
De variantie van een kansverdeling is gelijk aan:

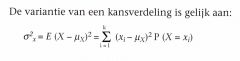
Back 81