![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
58 Cards in this Set
- Front
- Back
|
Boolesche Algebra als Körper |

Boolesche Algebra ist das Rechnen in der Restklasse ℤ₂ und da 2 eine Primzahl ist, ist (ℤ₂, +, · ) ein (kommutativer) Körper. |
|
|
Eine n-dimensionale boolesche Funktion in m Variablen. |
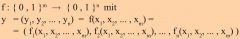
m und n ∈ N beliebig, aber beide ≠ 0 |
|
|
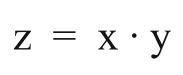
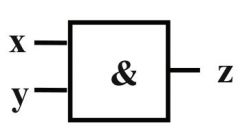
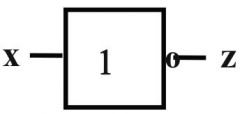
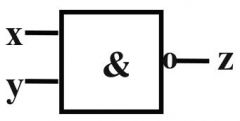
AND |
|
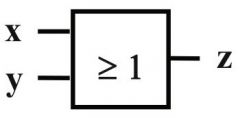
|
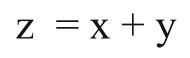
OR |
|
|
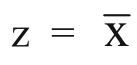
NOT |
|
|
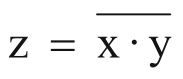
NAND
z wird 1 wenn: ¬(x = 1 ⋀ y = 1) |
|
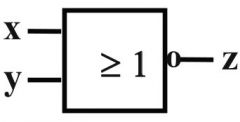
|
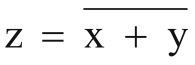
NOR
z wird 1 wenn: ¬(x = 1 ⋁ y = 1) |
|
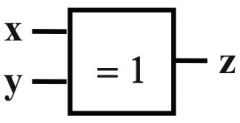
|
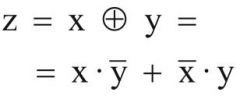
XOR
"genau eine 1" z wird 1 wenn: (x = 1 ⋀ y = 0) ⋁ (x = 0 ⋀ y = 1) |
|
|
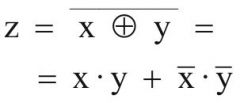
XNOR
z wird 1 wenn: (x = 0 ⋀ y = 0) ⋁ (x = 1 ⋀ y = 1) |
|
|
product term
|
x · y
Variables combined with boolean AND. |
|
|
sum of products (SOP) expression
|
x · y + a · b · c + f · g · h
A set of product terms combined with boolean OR. |
|
|
sum term
|
x + y
Variables combined with boolean OR. |
|
|
product of sums (POS) expression
|
(x + y) · (a + b + c) · (f + g + h) |
|
|
Minterm
|
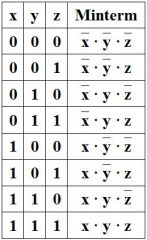
"Invert the 0 values, combine with AND." |
|
|
Minterm-Darstellung einer Funktion F(x, y, z)
|
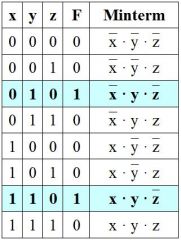
1) Minterm bestimmen für jede Kombination von Input Variablen, die 1 geben soll. |
|
|
Maxterm
|
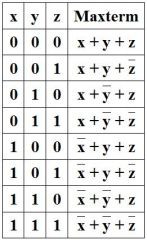
"Invert the 1 values, combine with OR." |
|
|
Maxterm-Darstellung einer Funktion F(x, y, z)
|
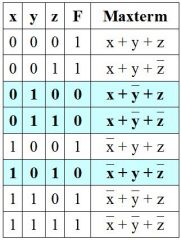
1) Maxterm bestimmen für jede Kombination von Input Variablen, die 0 geben soll. |
|
|
Nutzen von Minterm- und Maxterm-Darstellung
|
Sowohl die Minterm- als auch die Maxterm-Darstellung erlauben es, jede beliebige boolesche Funktion aufzubauen, nur mit AND, OR und NOT-Funktionen.
Beides sind logisch gleichwertige Alternativen. Man wählt natürlich diejenige Variante, die kürzer wird. Dies ist aber noch nicht unbedingt die einfachste Darstellung der Schaltung. Mit booleschen Gesetzen kann man möglicherweise weiter vereinfachen. |
|
|
Diese Funktion nur mit Hilfe von OR und NOT darstellen:
z = x AND y |
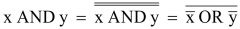
Trick: Doppelte Negation
|
|
|
Diese Funktion nur mit Hilfe von AND und NOT darstellen:
z = x OR y |
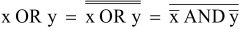
Trick: Doppelte Negation
|
|
Wieviele boolesche Funktionen gibt es bei 3 Input Bits und n Output Bits? |
2^3 Kombinationen von Input Bits, also 8. |
|
|
Boolesches Dualitätsprinzip
|
Boolesches Dualitätsprinzip: Falls man in einer gültigen booleschen Formel |
|
|
Assoziativgesetz
1. Form (Primärform) |
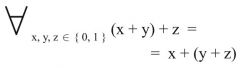
|
|
|
Assoziativgesetz
2. Form (Dualform) |
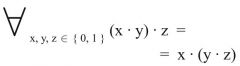
|
|
|
Kommutativgesetz
1. Form (Primärform) |
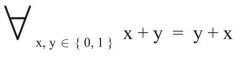
|
|
|
Kommutativgesetz
2. Form (Dualform) |
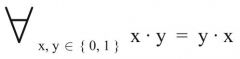
|
|
|
Distributivgesetz
1. Form (Primärform) |
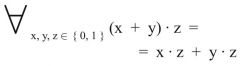
|
|
|
Distributivgesetz
2. Form (Dualform) ** WICHTIG ** |
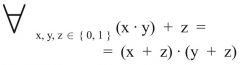
|
|
|
De Morgan
1. Form (Primärform) |
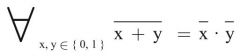
|
|
|
De Morgan
2. Form (Dualform) |
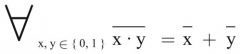
|
|
|
schwache Absorption
1. Form (Primärform) |
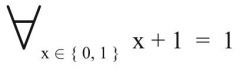
|
|
|
schwache Absorption
2. Form (Dualform) |
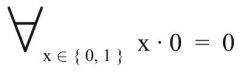
|
|
|
starke Absorption
1. Form (Primärform) ** WICHTIG ** |
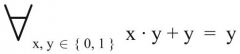
|
|
|
starke Absorption
2. Form (Dualform) ** WICHTIG ** |
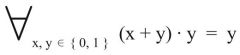
|
|
|
Involution |
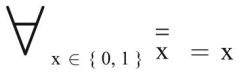
Primärform und Sekundärform sind bei Involution identisch. |
|
|
Involution
2. Form (Dualform) |
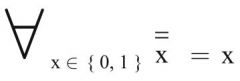
Sekundärform und Primärform sind bei Involution identisch.
|
|
|
Idempotenzgesetz
1. Form (Primärform) |
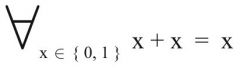
|
|
|
Idempotenzgesetz
2. Form (Dualform) |
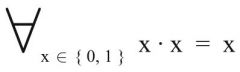
|
|
|
Gesetz vom Komplement
1. Form (Primärform) |
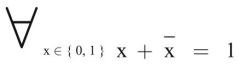
|
|
|
Gesetz vom Komplement
2. Form (Dualform) |
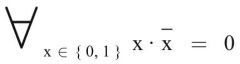
|
|
|
Gesetz der Redundanz
1. Form (Primärform) ** WICHTIG ** |
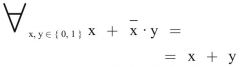
|
|
|
Gesetz der Redundanz
2. Form (Dualform) |
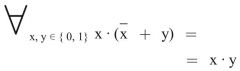
|
|
|
Konsensgesetz
1. Form (Primärform) ** WICHTIG ** |
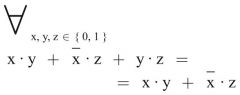
Beweis: |
|
|
Konsensgesetz
2. Form (Dualform) |
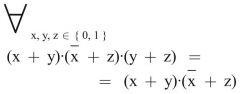
|
|
|
Neutrales Element
1. Form (Primärform) |

|
|
|
Neutrales Element
2. Form (Dualform) |
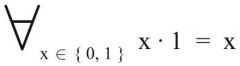
|
|
|
Minterm Expansion |
Each of the products that form the sum must be expanded so that it contains all variables. |
|
|
Maxterm Expansion |
Each of the sums that form the product must be expanded so that it contains all variables. |
|
|
Minimize from minterm form.
y = a'bc + ab'c' + ab'c + abc' + abc |
Look for differences in only one variable (= boolean adjacency). E.g. abc' is adjacent to abc and the two terms can be combined as ab(c' + c) using the distributive rule. |
|
|
MInimize from maxterm form.
y = (a + b + c)(a + b + c')(a + b' + c) |
Look for differences in only one variable.
(a + b + c)(a + b + c')(a + b' + c) = (a + b + cc')(a + b' + c) = (a + b)(a + b' + c) = (a + b)((a + c) + b') = (a + b)(a + c) + (a + b)b' = a + bc + ab + bb' = a + ab + bc = a(1 + b) + bc = a + bc Dualform Distributivgesetz: (a + b)(a + c) = a + bc |
|
|
Vereinfache
ab' + b |
ab' + b = a + b
Gesetz der Redundanz |
|
|
Vereinfache
(a + b)(b + a') |
(a + b)(b + a')
= ab + aa' + bb + ba' = ab + 0 + b + ba' = ab + a'b + 0 + b = (a + a')b + b = 1b + b = b + b = b |
|
|
Vereinfache
(a + b)' |
(a + b)'
= a'b' De Morgan (Primärform) |
|
|
Vereinfache
(ab)' |
a' + b' |
|
|
Vereinfache
f + fh' + g'f |
f + fh' + g'f |
|
|
Vereinfache |
(f + g'h')(g + h) |
|
|
Vereinfache |
(f + g)(f' + g' + h') |
|
|
Vereinfache |
f + fg' + fh + fg + gh |

