Mem 591

Front 1

Symmetric (Hermintian)

Back 1

AT=A

Front 2

Screw Symmetric

Back 2

AT=-A

Front 3

Orthagonal

Back 3

AtA=AAt=I

Front 4

Lower triangular

Front 5

a symmetric n-by-n matrix M is ________ if the scaler z^T*M*z is postive for every non-zero column vector z of n real numbers

Back 5

positive definite [2 -1 0;

-1 2 0;

0 -1 2]

Front 6

herminitian Matrix

Back 6

A^T=A

Front 7

skew herminitian

Back 7

A^T= -A

Front 8

orthagonal matrix

Back 8

(Q^T)Q=Q(Q^T)=I

Front 9

if the entries in a matrix above the main diagonal are zero the matrix is called

Back 9

lower triangular

Front 10

if the entries in a matrix below the main diagonal are all zero the matrix is called

Back 10

an upper triangular

Front 11

a square matrix is a called ________________ if it is invertable

Back 11

non-singular(invertible)

Front 12

a matrix that is not invertible is called a ______________

Back 12

singular matrix

Front 13

any of a number of results about linear operators or matrices

Back 13

spectral theorem

Front 14

_________________ for an inner product space V with finite dimension is a basis of V whose vectors are orthonormal, that is, they are all unit vectors and orthogonal to each other

Back 14

orthonormal basis

Front 15

a collection of objects called vectors which may be added together and multiplied by numbers called scalars

Back 15

vector space

Front 16

for every _____________ there exists a ______

Back 16

vector space there exists a basis

Front 17

the ________________ of a vector space V is the number of vectors of a basis of V

Back 17

dimension

Front 18

a set of vectors are linearly independent iff

Back 18

all the coefficients in the a1x1 + a2x2 + ... +anxn=0 equals 0

Front 19

this is a function that assigns a strictly positive length or size to each vector in a vector space

Back 19

norm

Front 20

the p-norm is equal to

Back 20

Front 21

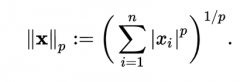
for a matrix norm ||A|| is

Back 21

greater than or equal to 0

Front 22

||A||=0 iff

Back 22

A=0

Front 23

||oA|| =

Back 23

|o|||A|| where o is a scaler

Front 24

||A+B|| ________||A|| + ||B||

Back 24

less than or equal to

Front 25

for all square matrices ||AB|| ____||A|| ||B||

Back 25

less than or equal to

Front 26

a factorization of a real or complex matrix and is the generalization of the eigendecompostion of a positive semidefinite normal matrix

Back 26

Singular Value Decomposition

Front 27

The uses of singular value decomposition

Back 27

signal processing and statistics, determination of the rank, range, and null space of a matrix

Front 28

a faster more economical computation of SVD

Back 28

reduced version of SVD

Front 29

If n<

Back 29

QR decomposition

Front 30

a decomposition of a matrix A into a product A=QR where Q =______ and R=_______

Back 30

Q=orthogonal matrix and R is a upper triangular matrix

Front 31

the rank of A is equal to the rank of

Back 31

the transpose of A

Front 32

the SVD can be useful because it can find the ______ of a matrix

Back 32

the rank

Front 33

lower triangular matrices can be solved by

Back 33

forward substitution

Front 34

upper triangular matrices can be solved by

Back 34

backward substitution

Front 35

_________ is the matrix form of Gaussian Elimination

Back 35

LU decomposition

Front 36

systems of linear equations are often solved by the

Back 36

LU decomposition

Front 37

any square matrix has a

Back 37

LUP factorization

Front 38

any matrix that is invertible, has a ________ factorization iff its leading principle minors are nonzero

Back 38

LU

Front 39

computing the LU decomposition requires how many steps

Back 39

2(n^3)/3

Front 40

It is faster and more efficient to compute the LU decomposition of a matrix A once and then solve the triangular matrices for the different b rather than performing

Back 40

Gaussian Elimination

Front 41

Once you have PA=LU you can use forward and backward substitution on the equations

Back 41

Ly=Pb and then Ux=y

Front 42

The advantage of LU decompostion over QR Decompostion

Back 42

LU is approximately 2(n^3)/3 steps and QR is approximately 4(n^3)/3 (LU IS TWICE AS FAST)

Front 43

a square binary matrix that has exactly one entry of 1 in each row and each column and 0's elsewhere

Back 43

permutation matrix

Front 44

the dimension of a rowspace is called ________

Back 44

the rank of the matrix

Front 45

elementary row operations have no effect on __________

Back 45

the rowspace of the matrix

Front 46

when a matrix is in rref the non zero rows are

Back 46

linearly independent

Front 47

the rank of the matrix is equal to _________ in rref

Back 47

number of non zero rows

Front 48

the rank of a matrix plus the dimension is equal to

Back 48

the number of columns

Front 49

in a matrix if the rows are linearly independent then the rank is equal to

Back 49

the amount of linearly independent rows

Front 50

the column space is key to

Back 50

existence of solutions

Front 51

the nullspace is the key to existence of

Back 51

uniqueness

Front 52

in general is the rank is equal to the nullspace

Back 52

the null(A) is equal to the zero vector and the solution to Ax=b (if there is one) is unique

Front 53

fewer equations than unknowns (r

Back 53

undetermined system (Infinitely many solutions)

Front 54

same number of equations as unknowns

Back 54

possibly one unique solution

Front 55

more equations than unknowns

Back 55

no solution

Front 56

the row space is ___________ to the nullspace

Back 56

perpendicular

Front 57

the column space is ___________ to the left nullspace

Back 57

perpendicular

Front 58

a matrix A is non singular iff

Back 58

i) A^-1 exists

ii) R(A)=R^n (dimR(A)=n)

iii) N(A)=0(vec)

iv) no zero eigenvalues

Front 59

if the rank of matrix A is equal to the num of rows and columns then

Back 59

the solution is unique

Front 60

if the rank is equal to the num of rows and less than the num of columns (norm >rows)

Back 60

there is an infinite amount of solutions

Front 61

if the rank is less than the number of rows and equal to the number of columns then

Back 61

there is 0 solutions if rows>col and 1 solution if N(A)=0

Front 62

if rank is less than both rows and columns then Ax=b has

Back 62

zero solutions

Front 63

one key applications of the SVD is

Back 63

the construction of low rank approximations to a matrix

Front 64

In a square matrix:

if the rank is = the number of rows and col

Back 64

there is a unique solution

Front 65

In a square matrix:

if the rank is less than the num of rows or columns then

Back 65

there are infinite solutions

Front 66

If there are more equations than unknowns then

Back 66

there is no solution

Front 67

the instability in the guass elimination method could be solved by

Back 67

permuting the order of the rows by pivoting

Front 68

the pivot is choosen by

Back 68

the largest absolute value in a subdiagonal entry in the column

Front 69

Gauss Elimination and Gauss Elimination Partial Pivoting is a

Back 69

direct method

Front 70

Iterative methods for Ax=b approximate solutions of a linear equation and find solutions that

Back 70

converge to an exact solution

Front 71

two types of iterative methods

Back 71

i) classical

ii) minimization algorithms

Front 72

if a matrix is _____________ then the Jacobi method converges for any initial guess x(0)

Back 72

strictly diagonally dominant

Front 73

classical iterative methods take advantage of the decomposition

Back 73

A=D+L+U

Front 74

three types of iterative methods

Back 74

Jacobian, Gauss Siegel, Successive over relaxation(SOR)

Front 75

methods that give solutions after an amount of computation that can be specified in advance

Back 75

direct methods

Front 76

iterative method

Back 76

starts from an approximation to the true solution and if successful obtain a better and better approximation from a computation cycle repeated as often as may be necessary for achieving required accuracy

Front 77

If matrices have large main diagonal entries, we use which method

Back 77

iterative methods

Front 78

you would use what method if your matrix is sparse or with many zeros in it and why?

Back 78

an iterative method because you wouldnt want to waste space storing zeros

Front 79

a sufficient condition for convergence in the gauss seidel method is

Back 79

||C||<1 where ||C|| = sqrt(sumj sumk cjk^2)

Front 80

Why is the gauss seidal a method of successive corrections?

Back 80

because for each component we successively replace an approximation of a component by a corresponding new approximation as soon as the latter has been computed

Front 81

What is a simultaneous correction iteration method?

Back 81

this is when no component of an approximation is used until ALL the components of x(m) have been computed (Jacobi iteration)

Front 82

the important facotrs in judging the quality of a numeric method are

Back 82

amont of storage

amount of time (number of operations)

effect of roundoff error

Front 83

minimization algorithms

Back 83

extremely useful techniques for solving large linear systems of equations

Front 84

advantages/disadvantages of direct methods

Back 84

they compute the exact solution but with high computational cost and (o(N^3)/3)

Front 85

advantages/disadvantages of iterative methods

Back 85

they converge to the exact solution with some tolerance they are faster with O(mn^2) but they are not garenteed to converge

Front 86

pivoting in the gauss elimination is unnecessary with what kind of matrices

Back 86

positive definite systems

Front 87

why can direct methods be bad

Back 87

direct methods could use a great deal of storage and perhaps computation time

Front 88

why isnt jacobis method used

Back 88

slowest iteration method

Front 89

in the Succession over relaxation, the acceleration factor is used to

Back 89

minimize the M0 and maximized the convergence rate