![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
24 Cards in this Set
- Front
- Back
|
Explain the process for adding vectors using their components.
|
First, find the components of each vector. For example, Vector A can be noted as (Ax, Ay). Next, add the x components of the vectors together. This sum is equal to the x component of the resultant. Next, add the y components of the vectors together. This sum is equal to the y component of the resultant. Write the resultant vector in component form. Then, use the x and y components as lengths for the legs of a right triangle where the hypotenuse is vector C. Finally, use the Pythagorean theorem to find the magnitude of vector C.
|
|
|
Find the sum of the vectors using their components.
|

A+B=C
A=(Ax,Ay) A=(2,2) B=(Bx,By) B=(1,2) Ax+Bx=Cx 2+1=3 Ay+By=Cy 2+2=4 C=(3,4) Cx²+Cy²=C² 3²+4²=C² C=5 |
|
|
Find the sum of the vectors using their components.
|

A+B=C
A=(Ax,Ay) A=(3,2) B=(Bx,By) B=(2,3) Ax+Bx=Cx 3+2=5 Ay+By=Cy 2+3=5 C=(5,5) Cx²+Cy²=C² 5²+5²=C² C=7.07 |
|
|
Explain the process for adding vectors using the parallelogram rule.
|
First, draw the two vectors with their tails at the same point. Next, add the two sides necessary to make a parallelogram. Last, start with the corner where the vectors' tails meet, and draw a line from this point to the opposite corner. This vector is A+B or vector C.
|
|
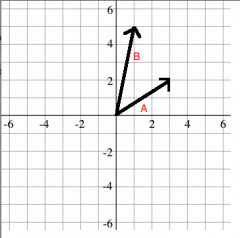
Show how to add these vectors using the parallelogram rule.
|

|
|

Show how to add these vectors using the parallelogram rule.
|
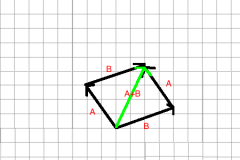
|
|
|
The magnitude of the sum of two vectors typically (is, is not) the sum of the magnitues.
|
The magnitude of two vectors typically is not the sum of the magnitudes.
|
|
|
Explain how to find the direction and magnitude of two vectors when they are stated in magnitude and direction form.
|
First, draw the two vectors tail-to-tail. Then, translate so the vectors are drawn head-to-tail and draw the resultant. Next, find the supplementary angle to find an angle of the triangle, then use the law of cosines to find the magnitude of the resultant vector. Finally, use the law of sines to find the direction of the resultant vector.
|
|
|
A vector u has a magnitude of 17m and a direction of 0deg. A vector v has a magnitude of 10m and a direction of 70deg. Find the direction and magnitude of u+v to the nearest whole values.
|
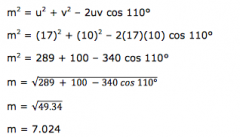
m²=u²+v²-2uv cos(110°)
m²=(17)² + (10)² - 2(17)(10)cos(110°) m²=289+100-340cos(110°) m=√289+100-340cos(110°) m=22.8 sin(110°)/22.8 = sinθ/10 θ=24.4° u+v= 22.8m @ 24.4° |
|
|
Vector subtraction can be shown by v-w. This expression can also be written as ________.
|
Vector subtraction can be shown by v-w. This expression can also be written as v+(-w).
|
|
|
When showing vector subtraction as v+(-w), what does (-w) represent?
|
(-w) represents the additive inverse of w. It is a vector with the same magnitude as w, but pointing in the opposite direction.
|
|
|
How can vector subtraction be represented graphically?
|
Vector subtraction can be represented graphically using the idea that, since a-b=a+(-b), vector b can be graphed as vector -b, which has the same magnitude as vector b, but in the opposite direction. Once graphed as such, vector addition is completed.
|
|
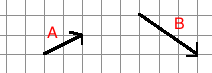
Represent subtraction of vector B from vector A graphically. Find the components of the resultant.
|
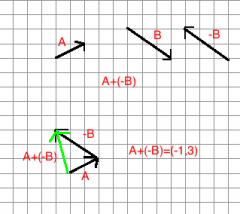
A-B=(-1,3)
|
|
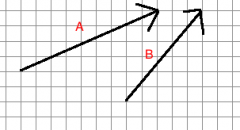
Represent subtraction of vector B from vector A graphically. Find the components of the resultant.
|
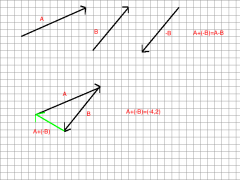
A-B=(-4,3)
|
|
|
Subtract vector b from a using their components. b=(5,7) a=(13,3)
|
a-b=a+(-b)
a+(-b)=(ax+(-bx),(ay+(-by)) a+(-b)=(5-13),(7-3) a+(-b)=(-8,4) |
|
|
subtract vector b from a using their components. b=(12,2) a=(2,8)
|
a-b=a+(-b)
a+(-b)=(ax+(-bx), ay+(-by)) a+(-b)=(12-2),(2-8) a+(-b)=(10,-6) |
|
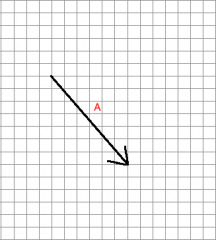
Represent the multiplication of vector A by -2 graphically.
|
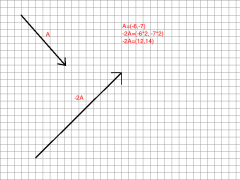
|
|
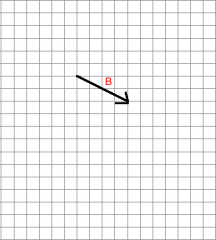
Represent the multiplication of vector B by 3.5
|
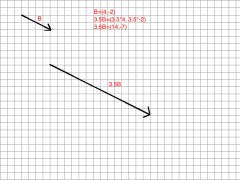
|
|
|
Multiply vector A by -4 using the components of vector A. A=(-6,14)
|
A=(-6,14)
-4A=(-6*-4, 14*-6) -4A=(24, -84) |
|
|
Multiply vector A by 1.75 using the components of vector A. A=(8,-4)
|
A=(8,-4)
1.75A=(8*1.75, -4*1.75) 1.75A=(14, -7) |
|
|
In vector notation, what is the meaning of ||cv||? What is another way this can be written?
|
||CV||means the scalar quantity C multiplied by the length (or norm) of vector V. This can also be written as |c|v
|
|
|
How does one find the magnitude and direction of the resultant of scalar C times vector V?
|
First, find the length (or norm) of vector V, then multiply this by the scalar quantity C to find the magnitude. The direction of CV is the same as the direction of vector V if C>0 and is the opposite as the direction of vector V if C<0.
|
|
|
Find the magnitude and distance of the resultant R of scalar C times vector V. C=-2 V=(3,4) @ 30deg
|
32+42=|V|2 9+16=|V|2 25=|V|2 |V|=5 ||CV||=-2*5 ||CV||=R Magnitude R=10 Direction R=-30deg because c<0.
*NOTE |V| does not represent the absolute value of V, but the norm (or length) of V. ||CV|| represents the norm (or length) of the product of CV. |
|
|
Find the magnitude and distance of the resultant R of scalar C times vector V. C=3 V=(2,6) @ 45deg
|
22+62=|V|2 4+36=|V|2 40=|V|2 |V|=6.325 ||CV||=3*6.325 ||CV||=18.974 Magnitude R=18.974, Direction R=45deg because c>0
|

