![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
10 Cards in this Set
- Front
- Back
|
The goal of this task is to explain why the area enclosed by a circle C of radius r is πr². Recall that π is the ratio of the circumference of a circle to its diameter and that this ratio is independent of the size of the circle.
A. Draw a picture of a regular octagon O inscribed in C. Find a formula for the area of the octagon in terms of its perimeter. |

Shown is a regular octagon whose vertices all lie on a given circle of radius r (fig.1). To find a formula for the area of this octagon, note first that the 8 triangles in the picture are all congruent: this follows, for example, from SAS since each triangle has two legs which are radii of the circle and all eight interior angles measure 45 degrees because the octagon is regular. Denoting one of these triangles, as T, the area of the octagon is 8T. To find the area of one of the triangles, draw a new picture (without the circle) (fig.2), showing an altitude of one of the triangles. The area of T is 1/2*base*height. In the picture, the base is b and the height is a, so the area of the regular octagon is 8*area(T) = 8(1/2ba) = (8b)(a/2) = 8*Perimeter(octagon)*(a/2).
|
|
|
The goal of this task is to explain why the area enclosed by a circle C of radius r is πr². Recall that π is the ratio of the circumference of a circle to its diameter and that this ratio is independent of the size of the circle. B. Reasoning as in part A, find a formula for the area of a regular n sided polygon, for n≥3, inscribed in C: the formula should give you the area of the polygon in terms of its perimeter.
|
We can decompose our regular polygon Pⁿ with n sides into n congruent triangles as in part A. We denote one of these triangles by Tⁿ. We can then duplicate the reasoning at the end of part A to find the area of Pⁿ. For this, we let bⁿ denote the length of the base of Tⁿ and aⁿ its height.
Area(Pⁿ)= n*Area(Tⁿ) = n* (1/2bⁿ*aⁿ) = (n*bⁿ)* aⁿ/2 = Perimeter(Pⁿ)* aⁿ/2 |
|
|
The goal of this task is to explain why the area enclosed by a circle C of radius r is πr². Recall that π is the ratio of the circumference of a circle to its diameter and that this ratio is independent of the size of the circle. C. Using your formula from part B, explain why the area of C is πr².
|
As the number of sides on our polygon Pⁿ increases, the perimeter of Pⁿ will approach the circumference of C while the distance an from the center of the circle to the sides of Pⁿ will approach the radius r of C. Finally, the area of Pⁿ approaches the area of C. Putting this all together, we get:
Area(C)= circumference(C)*r/2. Since the circumference of C is 2πr, this is the same as Area(C)=2πr*r/2 = πr². |
|
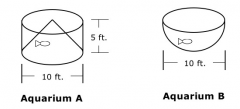
The management of an ocean life museum will choose to include either Aquarium A or Aquarium B in a new exhibit. Aquarium A is a right cylinder with a diameter of 10 feet and a height of 5 feet. Covering the lower base of Aquarium A is an "underwater mountain" in the shape of a 5 foot tall right cone. This aquarium would be built into a pillar in the center of the exhibit room. Aquarium B is half of a 10 foot diameter sphere. This aquarium would protrude from the ceiling of the exit room. A. How many cubic feet of water will Aquarium A hold?
|
volume of Cylinder - volume of cone = maximum volume of water for aquarium A
(πr²*h) - (1/3πr²h) = 2/3πr²h = 2/3(π)(5²)(5) = 250π/3 ≈ 262 Aquarium A can hold approximately 262 cubic feet of water. |
|
|
The management of an ocean life museum will choose to include either Aquarium A or Aquarium B in a new exhibit. Aquarium A is a right cylinder with a diameter of 10 feet and a height of 5 feet. Covering the lower base of Aquarium A is an "underwater mountain" in the shape of a 5 foot tall right cone. This aquarium would be built into a pillar in the center of the exhibit room. Aquarium B is half of a 10 foot diameter sphere. This aquarium would protrude from the ceiling of the exit room. B. For each aquarium, what is the area of the water's surface when filled to a height of h feet?
|
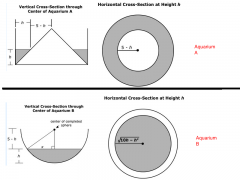
The area of the water's surface at height h can be derived by examining cross-sections. The radius and height of the cylinder and cone are both 5, so the vertical cross section through the vertex of the cone shown here shows that the cross setction of the water forms an isoceles right triangle. Therefore, the horizontal distance between the cone and the aquarium at height h is also h. The area of the water's surface at height h is found by subtracting the area of the inner circle, with radius 5-h from the area of the outer circle, with radius 5. π*5² - π* (5-h)²= 25π-π(25-10h+h²) = 25π -25π+10πh-πh² = 10πh-πh² When Aquarium A is filled to a height of h feet, the area of the water's surface is 10PIh-PIh2 square feet. Aquarium B: Momentarily, the horizontal distance between the curved wall and the sphere's center at height h is denoted by x. But x can be expressed in terms of h, since x and 5-h both represent leg lengths of a right triangle with hypotenuse 5: x²+(5-h)²=25 x²+25-10h+h²=25 x²=10h-h² x=√10h-h². In this case, the area of the water's surface at height h is simply the area of a circle whose raidus is √10h-h²: Area =π(√10h=h²)² = π(10h-h²) = 10πh-πh².
|
|
|
The management of an ocean life museum will choose to include either Aquarium A or Aquarium B in a new exhibit. Aquarium A is a right cylinder with a diameter of 10 feet and a height of 5 feet. Covering the lower base of Aquarium A is an "underwater mountain" in the shape of a 5 foot tall right cone. This aquarium would be built into a pillar in the center of the exhibit room. Aquarium B is half of a 10 foot diameter sphere. This aquarium would protrude from the ceiling of the exit room. C. Use your results from parts A and B and Cavalieri's principle to find the volume of Aquarium B.
|
Cavalieri's principle states that two 3-dimensional solids of the same height are equal in volume if the areas of their horizontal cross-sections at every height h are equal. Since both aquariums stand 5 feet tall, and since the area of the water's surface when filled to a height of h for each aquarium, the volumes of water must be equal when both aquariums are filled to full capacity according to the principle. Therefore, no further calculations are necessary to determin that Aquarium B will hold 250π/3 ≈ 262 cubic feet of water, the same volume that Aquarium A will hold.
|
|

Find the volume of this figure.
|
V=πr²h
V=π(6²)(6) V=216π V=678.58 in³ |
|
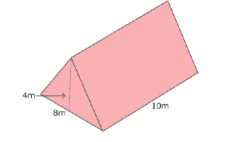
Find the volume of this figure.
|
V= 1/2*base*height*length
V=1/2(8)(4)(10) V=160 m³ |
|
Find the volume of this figure.
|
V=1/3πr²h
V=1/3(π)(6²)(9) V=108π V=339.29 in³ |
|
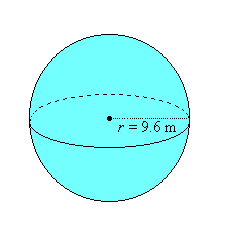
Find the volume of this figure.
|
V=4/3πr³
V=4/3π(9.6³) V=1179.648π V=3705.97 m³ |

