High School Common Core Mathematics

Front 1

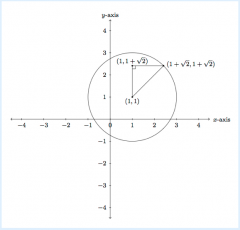
Use the Pythagorean theorem to find an equation in x and y whose solutions are the points on the circle of radius 2 with center (1,1) and explain why it works. Use the given picture to help you.

Back 1

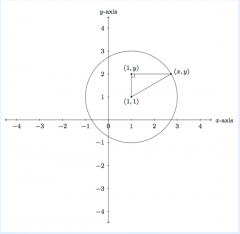
The circle of radius 2 with center (1,1) is pictured. To get a feel for how to apply the Pythagorean theorem in this setting, a point (1+√2, 1+√2) has also been labelled on the circle. A third point (1,1+√2) has been added, making a right triangle along with the center of the circle and the point (1+√2, 1+√2). The Pythagoream theorem tells us that the sum of the squares of the legs of this triangle is equal to the square of the hypotenuse. (√2)²+(√2)²=2². More generally, if (x,y) is any point on the circle of radius 2 centered at (1,1) then this means that the distance from (x,y) to (1,1) is 2, as seen in the picture. The lengths of the legs of the triangle are caluclated using |x-1| for the horizontal and |y-1| for the vertical. The hypotenuse has length 2 because (x,y) lies on the circle of radius 2 and center (1,1). By the Pythagorean theorem, (x-1)²+(y-1)²=2². The absolute value signs are not necessary here because (x-1)²= |x-1². So every point (x,y) on the circle of radius 2 with center (1,1) satisfies the equation (x-1)²+(y-1)²=2².

Front 2

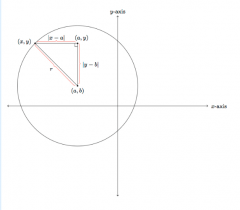
Suppose r is a positive number and (a,b) a point in the plane. Use the Pythagorean theorem to find an equation in x and y whose solutions are points on the circle of radius r with center (a,b) and explain why it works. Use the given picture to help you.

Back 2

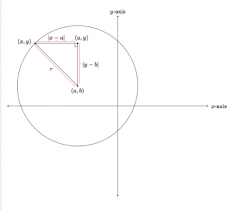
The lengths of the legs are found using |x-a| and |y-b|. The length of the hypotenuse is given, r. By the Pythagorean theorem, (x-a)²+(y-b)²=r². The absolute value signs are not necessary in the equation because (x-a)²=|x-a|² and (y-b)²=|y-b|². So every point (x,y) on the circle of radius r with center (a,b) satisfies the equation (x-a)²+(y-b)²=r². Conversely, with the exceptions of (a,b+r), (a,b-r), (a-r,b) and (a+r,b), every pair (x,y) satisfying the equation (x-a)²+(y-b)²=r² gives a triangle as above and a point on the circle with radius r and center (a,b): the Pythagorean theorem tells us that if (x,y) satisfies this equation then it is a distance r from (a,b) and is therefore on the circle of radius r and center (a,b). The four exceptional cases noted above also lie on the circle of radius with center (a,b) but there is no triangle in this case, just a line segment of length r.

Front 3

Suppose A=(a₁,a₂) and B=(b₁,b₂) are two points in the plane, determined by constants a₁, a₂, b₁, b₂. Suppose X=(x₁,x₂) is a third point, determined by the variables x₁ and x₂. Write an expression that gives the slope of line AX in terms of a₁, a₂, x₁, x₂. Write an expression that gives the slope of line BX in terms of b₁, b₂, x₁, x₂.

Back 3

For line AX, the slope can be found using m=(a₂-x₂)/(a₁-x₁) and for line BX, the slope can be found using m=(b₂-x₂)(b₁-x₁).

Front 4

Suppose A=(a₁,a₂) and B=(b₁,b₂) are two points in the plane, determined by constants a₁, a₂, b₁, b₂. Suppose X=(x₁,x₂) is a third point, determined by the variables x₁ and x₂. Write a polynomial equation involving a₁, a₂, b₁, b₂, x₁, x₂ that expresses that the lines AX and BX are perpendicular.

Back 4

Using the slope criterion for perpendicularity,
AX⊥BX
m(AX)*m(BX)=-1
(a₂-x₂)/(a₁-x₁) * (b₂-x₂)/(b₁-x₁)=-1
(a₂-x₂)(b₂-x₂)=(-1)(a₁-x₁)(b₁-x₁)
This equation is equivalent to:
0=x²₁-(a₁+b₁)x₁+a₁b₁+x²₂-(a₂b₂)x₂+a₂b₂

Front 5

Suppose A=(a₁,a₂) and B=(b₁,b₂) are two points in the plane, determined by constants a₁, a₂, b₁, b₂. Suppose X=(x₁,x₂) is a third point, determined by the variables x₁ and x₂. What geometric figure is the solution set of the polynomial equation you created? 0=x²₁-(a₁+b₁)x₁+a₁b₁+x²₂-(a₂b₂)x₂+a₂b₂

Back 5

The equation 0=x²₁-(a₁+b₁)x₁+a₁b₁+x²₂-(a₂b₂)x₂+a₂b₂ can be transformed by completing the square and simplifying to:
(a₁-b₁/2)²+(a₂-b₂/2)²=(x₁-(a₁+b₁/2))²+(x₂-(a₂+b₂/2))².
By the distance formula (or by the Pythagorean theorem), the left side is the square of half the length of segment AB. The constants a₁+b₁/2 and a₂+b₂/2 on the right are the coordinates of the midpoint of segment AB. Thus, the solution of the equation is the circle of raidus |AB|/2, with center at the midpoint of segment AB.

Front 6

If the focus of a parabola is (0,-2) and the directrix is y-2, find the equation of the parabola.

Back 6

The distance between (x₀,y₀) and (0,-2) is √(x₀-0)²+(y₀-(-2))². The distance between (x₀,y₀) and the directrix, y=2, is |y₀=2|.
Equate the two distance expressions and square on both sides.
√(x₀-0)²+(y₀-(-2))²=|y₀-2| (x₀-0)²+(y₀-(-2)²=(y₀-2)².
Simplify and bring all terms to one side to get
(x₀)²+4y₀+4y₀=0.
Write the equation with y₀ on one side to get
y₀=(-x₀)²/8.
This equation in (x₀,y₀) is true for all other values on the parabola and hence we can rewrite it with (x,y). So the equation of a parabola with focus (0,-2) and directrix y=2 is y=-x²/8.

Front 7

If the focus of a parabola is (5,-1) and the directrix is y=3, find the equation of the parabola.

Back 7

The distance between (x₀,y₀) and (5,-1) is √(x₀-5)²+(y₀-(-1))². The distance between (x₀,y₀) and the directrix, y=3, is |y₀=3|. Equate the two distance expressions and square on both sides.
√(x₀-5)²+(y₀-(-1))²=|y₀-3| (x₀-5)²+(y₀-(-1)²=(y₀-3)²
Simpify and bring all terms to one side to get
(x₀)²+10x₀+17+8y₀=0
Write the equation with y₀ on one side to get
y₀=(-x₀)²/8+10x₀-17.
This equation in (x₀,y₀) is true for all other values on the parabola and hence we can rewrite it with (x,y). So the equation of a parabola with focus (5,-1) and directrix y=3 is y=-x²/8+10x-17.

Front 8

Find the equation of an ellipse in standard form that has vertices at (0,-6 and (0,6) and foci at (0,-13) and (0,13).

Back 8

Standard from for an equation of an ellipse is (x-h)²/a²+(y-k)²/b²=1. To write the equation in standard form, the center, a² and b², must be found. The x-coordinates of the vertices and foci given are 0, so the center or the ellipse must be (0,0). Since the foci are 26 units apart, the vertices (0,-6) and (0,6) are on the minor axis of the ellipse indicating that |b| is 6 and b², then, is 36. To find a², use the foci equation. C is the distance from the center of the ellipse to the foci. Since the center is (0,0) and the foci are (0,-13) and (0,13), C=13. C²=|a²-b²| 13²=|a²-(6)²| 169=|a²-36| -169=a²-36 +169=a²-205 √205=a (discard -133=a² as a solution because it is negative). Substitute 0 for h and k, √205 for a and 6 for b.
(x-0)²/(√205)²+(y-0)²/(6)²=1
x²/205+y²/36=1

Front 9

Find an equation of the hyperbola with x-intercepts at x=-8 and x=6 and foci at (-7,0) and (5,0)

Back 9

The genereal form of the equation for a hyperbola is (x-h)²/a²+(y-k)²/b²=1, where (h,k) is the center, a is the semi-transverse axis, and b is the semi-conjugate axis. If we look at the foci, we will see that they are side by side. This indicates that branches of the hyperbola follow this lead. This also means that the center, foci, and vertices are on a line that is parallel to the x-axis. We know the center is in the middle of the foci, in this case (h,k)=(-1,0). We also know that the foci are offset from the center, so, in this case c=8 and c²=64. Finally, we know that the center resides on the x-axis. This means that the x-intercepts have to also be vertices for the hyperbola. So, a=5 and a²=25. By the Pythagorean theorem a²+b²=c² we can solve for b=39. Therefore, the equation is (x+1)²/25-y²/39=1

Front 10

Using the distance formula, find the perimeter of the given geometric figure.

Back 10

d=√(x₂-x₁)²+(y₂-y₁)²
For points A&B: d=√(-7-(-9))²+(-4-(-7))²
d= √(2²+3²
d=√13 d≈3.61
For points B&C: d=√(3-(-7))²+(3-(-4))²
d=√10²+7²
d=√149 d≈12.21
For points C&D: d=√(5-3)²+(0-3)²
d=√(2+(-3)²
d=√13 d≈3.61
For points D&E: d=√(0-5)²+(-12-0)²
d=√(-5)²+(-12)²
d=√169 d=13
For points E&A d=√(-9-0)²+(-7-(-12))²
d=√(-9)²+5²)
d=√106 d≈10.30
P=AB+BC+CD+DE+EA
P=3.61+12.21+3.61+13+10.30 P=42.73