High School Common Core Mathematics

Front 1

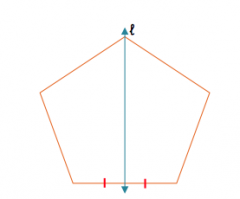
Describe the transformation would carry this regular polygon onto itself.

Back 1

Since n=5 is odd and l passes through a vertext and the midpoint of its opposite side, l is a line of symmetry. So, one answer is, reflection across l. Rotating a regular hexagon by a multiple of (360/5=) 72° carries the hexagon onto itself, so the second answer is, a rotation of 72° clockwise.

Front 2

Which type of transformation would carry this regular polygon onto itself?

Back 2

Rotating a regular hexagon by a multiple of (360/6=) 60° carries the hexagon onto itself.

Front 3

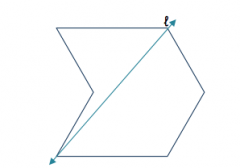
Describe the transformation that would carry this regular polygon onto itself.

Back 3

Rotating a regular triangle by a multiple of (360/3=) 120° carries the triangle onto itself.

Front 4

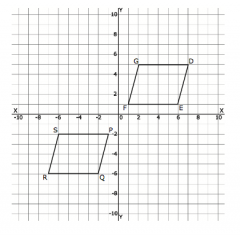
Use the definition of congruence in terms of rigid motions to determine whether DEFG and PQRS are congruent and explain your answer.

Back 4

DEFG and PQRS are congruent becasue all points of DEFG can be translated 9 units left and 7 units up [T(9,7)] to form PQRS.

Front 5

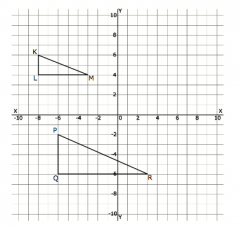
Are triangles KLM and PQR congruent? Explain using the definition of congruence in terms of rigid motions.

Back 5

Triangles KLM and PQR are not congruent because there is no sequence of rigid motions that will map KLM to PQR. All rigid motions preserve size, and KLM and PQR are not the same size, so they cannot be congruent.

Front 6

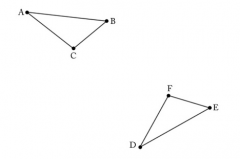
In these two triangles, angle A is congruent to angle D, side AC is congruent to side DF and side AB is congruent to side DE. Sally reasons that, "If angle A is congruent to angle D then I can move point A to point D so that side AB lies on top of side DE and side AC lies on top of side DF. Since AB and DE are congruent as are AC and DF the two triangles match up exactly and so they are congruent." Explain Sally's reasoning for why triangle ABC is congruent to triangle DEF by constructing a reflection which maps point A to point D. Call B' and C' the images of B and C respectively.

Back 6

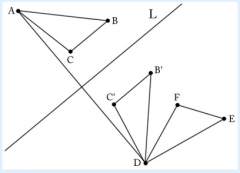
We wish to send A to D via reflection, so we must reflect about the perpindicular bisector of AD. Triangle DB'C' is created by this reflection.

Front 7

Point A has been moved to point D via reflection. The new triangle is DB'C'. Construct a reflection which does not move D but which sends B' to E. Call C" the image of C' under this reflection.

Back 7

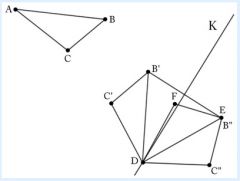
We must reflect DB'C' over the perpindicular bisector of B'E. It is important that this perpindicular bisector (K) contains point D so that point D does not move. We know that D is on the perpindicular bisector of B'E is because it is equidistant from E and B' by the hypothesis that AB is congruent to DE. The result of this second reflection is triangle DEC".

Front 8

Triangle DEC" has been constructed from a series of reflections. Construct a final reflection which does not move point D or E but which sends C" to F.

Back 8

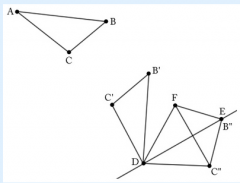
C" must be moved to F via reflection while D and E stay fixed. The only reflection that leaves D and E fixed is one over line DE. Angle FDE is congruent to angle C"DE because angle C"DE is the image under two reflections of angle CAB which is congruent to angle FDE by hypothesis, segment DF is congruent to segment AC by hypothesis and AC is congruent to DC", therefore the reflection about line DE maps C" to F'. After this series of reflections, triangle ABC has been moved on top of triangle DEF so the two are congruent.

Front 9

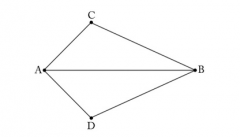
In triangles ABC and ABD, we are given that angle BAC is congruent to angle BAD and angle ABC is congruent to angle ABD. Show that the reflection of the plane about line AB maps triangle ABD to triangle ABC.

Back 9

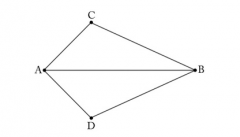
D' is the image of D under the reflection about line AB. Since reflection about a line is a rigid motion, it preserves both distances and angles. Since angle DAB is congruent to angle CAB by hypothesis, we can conclude that angle D'AB is congruent to angle CAB. Since these two angles are congruent, share ray AB and are both above line AB, we must have that ray AD' is the same as ray AC. In particular, we see that D' lies on ray AC. Reasoning in the same way with congruent angles D'BA and CBA shows that D' also lies on ray BC. We know, however, that rays AC and BC meet in exactly one point, namely C, so this establishes that D'=C. Since reflection about line AB fixes points A and B, the triangle ABD has been mapped via reflection to triangle ABC and consequently these two triangles are congruent.

Front 10

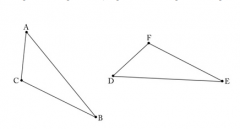
In this picture, segment AB is congruent to segment DE, segment AC is congruent to segment DF and segment BC is congruent to segment EF. Show that the two triangles ABC and DEF are congruent through a series of rigid transformations of the plane sending triangle ABC to triangle DEF. STEP 1: Show that there is a translation of the plane which maps A to D. Call B' and C' the images of B and C under this transformation.

Back 10

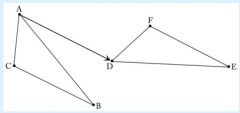
Translation by the segment AD maps A to D. This transformation creates triangle DB'C'.

Front 11

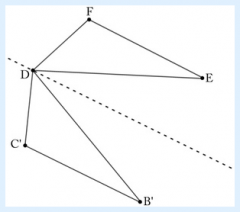
In this picture, segment AB is congruent to segment DE, segment AC is congruent to segment DF and segment BC is congruent to segment EF. Show that the two triangles ABC and DEF are congruent through a series of rigid transformations of the plane sending triangle ABC to triangle DEF. STEP 2: show that there is a rotation of the plane which does not move D and which maps B' to E. Call C" the image of C' under this transformation.

Back 11

In order to move B' to E without moving D, rotate triangle DB'C' about point D by angle B'DE, creating triangle DEC"

Front 12

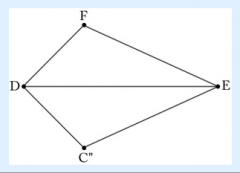
In this picture, segment AB is congruent to segment DE, segment AC is congruent to segment DF and segment BC is congruent to segment EF. Show that the two triangles ABC and DEF are congruent through a series of rigid transformations of the plane sending triangle ABC to triangle DEF. STEP 3: Show that there is a reflection of the plane which does not move D or E and which maps C" to F.

Back 12

The only possible rigid motion of the plane other than the identity, which does not move D or E, is reflection about the line DE, which moves point C" to point F, therefore finishing mapping triangle ABC to triangle DEF.