![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
22 Cards in this Set
- Front
- Back
|
Subset
|
A is a _______ of B only if every element of A is also an element of B.
|
|
|
proper subset
|
A is a ______ ______ of B only if every element of A is in B but there is at least one element of B that is not in A.
|
|
|
A = B if...
(sets) |
A _____ B only if every element of A is in B and every element of B is in A.
|
|
|
The union of A and B
Let A and B be subsets of a universal set U. |
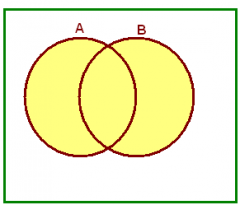
The set of all elements x in U such that x is in A or x is in B.
|
|
|
The intersection of A and B
Let A and B be subsets of a universal set U. |
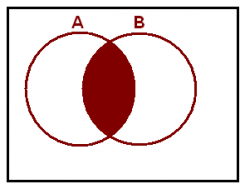
The set of all elements x in U such that x is in A and x is in B.
|
|
|
The difference of A-B
(Or relative complement of B in A) Let A and B be subsets of a universal set U. |
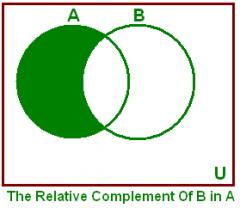
The set of all elements x in U such that x is in A and x is not in B.
|
|
|
The complement of A
Let A and B be subsets of a universal set U. |
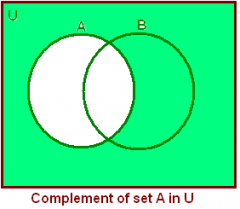
The set of all elements x in U such that x is not in A.
|
|
|
∼(p ∧ q) ≡ ....
|
.... ≡ ∼p ∨ ∼q
The negation of an and statement is logically equivalent to the or statement in which each component is negated. |
|
|
∼(p ∨ q) ≡ ....
|
.... ≡ ∼p ∧ ∼q
The negation of an or statement is logically equivalent to the and statement in which each component is negated. |
|
|
p →q
|
It is false when p is true and q is false;
*otherwise it is true* |
|
|
p →q ≡ ....
|
.... ≡ ∼p ∨ q
|
|
|
∼(p →q) ≡ ....
|
.... ≡ p ∧ ∼q
The negation of “if p then q” is logically equivalent to “p and not q. |
|
|
The contrapositive of p →q is ....
∀x ∈ D, if P(x) then Q(x). A conditional statement is logically equivalent to its contrapositive. |
.... of p →q is ∼q →∼p.
.... ∀x ∈ D, if ∼Q(x) then ∼P(x). |
|
|
The converse of p →q is ....
∀x ∈ D, if P(x) then Q(x). 1. A conditional statement and its converse are not logically equivalent. 3. The converse and the inverse of a conditional statement are logically equivalent to each other. |
The.... of p →q is q → p,
∀x ∈ D, if Q(x) then P(x) |
|
|
The inverse of p →q is ....
∀x ∈ D, if P(x) then Q(x). 2. A conditional statement and its inverse are not logically equivalent. 3. The converse and the inverse of a conditional statement are logically equivalent to each other. |
The .... of p →q is ∼p →∼q
∀x ∈ D, if ∼P(x) then ∼Q(x) |
|
|
biconditional of p and q is ...
|
“p if, and only if, q” "p ↔ q"
It is true if both p and q have the same truth values and is false if p and q have opposite truth values. |
|
|
∼(∀x ∈ D, Q(x)) ≡ ....
|
.... ≡ ∃x ∈ D such that ∼Q(x).
|
|
|
∼(∃x ∈ D such that Q(x)) ≡ ....
|
.... ≡ ∀x ∈ D,∼Q(x).
|
|
|
∼(∀x, if P(x) then Q(x)) ≡ ....
|
.... ≡ ∃x such that P(x) and ∼Q(x).
|
|
|
Even and Odd
|
Symbolically, if n is an integer, then
n is even ⇔ ∃an integer k such that n = 2k. n is odd ⇔ ∃an integer k such that n = 2k + 1. |
|
|
Prime/Composite
|
In symbols:
n is prime ⇔ ∀positive integers r and s, if n = rs then either r = 1 and s = n or r = n and s = 1. n is composite ⇔ ∃positive integers r and s such that n = rs and 1 < r < n and 1 < s < n. |
|
|
Proofs
|
1. Copy the statement of the theorem to be proved on your paper.
2. Clearly mark the beginning of your proof with the word Proof. 3. Make your proof self-contained. 4. Write your proof in complete, gramatically correct sentences. 5. Keep your reader informed about the status of each statement in your proof. 6. Give a reason for each assertion in your proof. 7. Include the “little words and phrases” that make the logic of your arguments clear 8. Display equations and inequalities. |

