![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
37 Cards in this Set
- Front
- Back
- 3rd side (hint)
|
DISTANCE FORMULA |p1, p2|
|
√(x2 - x1)² + (y2 - y1)² + (z2 - z1)²
|
2 minus 1
|
|
|
Equation of a Sphere with center (h,k,l) and radius r
|
(x - h)² + (y - k)² + (z - l)² = r²
|
|
|
|
vector
|
a quantity that has both magnitude and direction
|
|
|
|
vector components
|
<a1, a2, a3>
|
|
|
|
Definition of vector addition
|
If a and v are vectors positioned so the initial point of v is at the terminal point of a then the sum u + v is the vector from the initial point of u to the terminal point of v.
PQ + QR = PR QS - PS = QP |
|
|
|
Properties of vectors
|
a + b = b + a
a + (b + c) = (a + b) + c a + 0 = a a + -a = 0 scalar-c(a + b) = ca + cb scalars(c + d)a = ca + da scalars(cd)a = c(da) 1a = a |
|
|
|
standard basis vectors
|
i <1,0,0>
j <0,1,0> k <0,0,1> |
|
|
|
unit vectors
|
a vector whose length is 1
(standard basis vectors) |
|
|
|
resultant force
|
the vector sum of several forces acting on an object
|
|
|
|
position vector
|
the representation of a vector from the origin.
Given 2 points a = <x2 - x1, y2 - y1, z2 - z1> |
|
|
|
Magnitude or length of a vector
|
|a| = √a1² + a2² + a3²
|
|
|
|
Adding vectors algebraically
|
a + b = <a1 + b1, a2 + b2, a3 + b3>
|
|
|
|
dot product
|
a ∙ b = (a1)(b1) + (a2)(b2) + (a3)(b3)
|
|
|
|
Properties of the dot product
|
a ∙ a = |a|²
a ∙ b = b ∙ a a ∙ (b + c) = a ∙ b + a ∙ c (ca) ∙ b = c(a ∙ b) = a ∙ (cb) 0 ∙ a = 0 |
|
|
|
Theorem 3 If Θ is the angle between vectors a and b
|
a ∙ b = |a| |b| cos Θ
cos^-1 Θ = a ∙ b ∕ |a| |b| |
|
|
|
Scalar projection of b onto a
|
comp(a) b = a ∙ b / |a|
|
|
|
|
vector projection of b onto a
|
proj a b = (a ∙ b / |a|²) ( a)
|
|
|
|
Work/Force/Distance Equation
|
W = F ∙ D if no angle
or w = |F||D| cos Θ |
|
|
|
Theorem 4 If Θ is the angle between a and b then
|
|a x b| = |a| |b| sin Θ
or sin^-1 Θ = |a x b| / |a| |b| |
|
|
|
x²/a² + y²/b² + z²/c² = 1
|
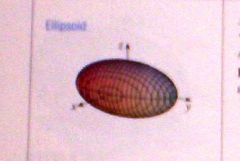
Ellipsoid
|
(3)2nd order terms and a constant)
|
|
|
z²/c² = x²/a² + y²/b²
|
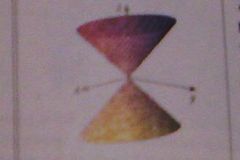
Cone
|
(3)2nd order variables
No constants. If put in form x²/a² + y²/b² - z²/b² = 0 - Opens towards axis of negative variable. |
|
|
z/c = x²/a² + y²/b²
|
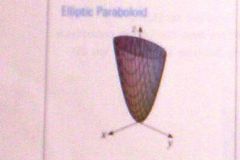
Elliptic paraboloid
|
(2)2nd order terms that have same sign.
(1)1st order term. No constants. Opens along 1st order term axis. 2nd order terms determines + or -. |
|
|
z/c = x²/a² - y²/b²
|
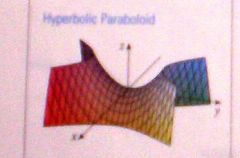
Hyperbolic Paraboloid
|
(2)2nd order terms that have opposite signs.
(1)1st order term. No constants. Neg 2nd order term = head of horse. 1st order term = top of saddle. |
|
|
x²/a² + y²/b² - z²/c² = 1
|

Hyperboloid of one sheet
|
(3)2nd order terms
(1) constant (1) negative term - opens along this term |
|
|
-x²/a² - y²/b² + z²/c² = 1
|

Hyperboloid of two sheets
|
(3) 2nd order terms
(1) constant (1) positive term - opens along this term |
|
|
x² + y² = 1
|
Cylinder
|
(2) variables
extruded along missing variable |
|
|
vector equation of a line
|
r = rօ + t(v)
r = (x,y,z) + t<a,b,c> |
|
|
|
parametric equations
|
x = xօ + at
y = yօ + bt z = zօ + ct |
|
|
|
symmetric equations
|
(x - xօ)/a = (y - yօ)/b = (z - zօ)/c
|
|
|
|
vector equation of a plane
|
n ∙ r = n ∙ rօ
or n ∙(r - rօ) = 0 |
|
|
|
scalar equation of a plane
|
a(x - xօ) + b(y - yօ) + c(z - zօ) = 0
|
|
|
|
normal vector
|
vector orthogonal to a plane
|
cross product
|
|
|
linear equation of a plane
|
ax + by + cz + d = 0
|
|
|
|
parallel planes
|
normal vectors are parallel
|
|
|
|
Distance from point to a plane
|
|ax₁ + by₁ + cz₁ + d|/√a² + b² + c²
|
|
|
|
Area of a parallelogram
|
|a x b|
|
|
|
|
volume of a parallelepiped
|
|a ∙ (b x c)|
|
|

