![]()
![]()
![]()
Use LEFT and RIGHT arrow keys to navigate between flashcards;
Use UP and DOWN arrow keys to flip the card;
H to show hint;
A reads text to speech;
78 Cards in this Set
- Front
- Back
|
ArrayList - Aufwand (size, at, push_back, insert, pop_back, erase) |
O(1, 1, 1*, n, 1, n) |
|
|
Singly - Aufwand (size, at, pushback, insert, popback, erase, front, push_front, pop_front) |
O(n, n, n, n, n, n, 1, 1, 1) |
|
|
ArrayList vs Linked List |
ArrayList + hinten anhängen & entfernen + Speicher, da basierend auf Feld Linked + Vorne anhängen & entfernen - Kein kontinuierlicher Speicherblock sondern "Fragmente" |
|
|
Doubly - Aufwand (size, front/back, at, push_front/back, insert, pop_front/back, erase) |
O(n ,1, n, 1, n, 1, n) |
|
|
Doubly Linked List - Member |
- Node Klasse mit Data, Prev & Next - Head - Tail |
|
|
Singly Linked List - Member |
- Node Klasse mit Data & Next - Head |
|
|
Iterator Interface Specs |
- Traviersieren von Daten - Iterator // CTor - hasNext() // is done or not - next() // return current & move to next - remove() // Legacy |
|
|
Binärbaum (n-är-Baum) |
Jeder Knoten höchstens zwei (n) Kinder |
|
|
Voller Baum |
Jeder Knoten entweder 0 (Blätter) oder 2 Kinder |
|
|
Vollständiger Baum |
Alle Blätter (Kinder) auf einer Ebene |
|
|
Baum - Höhe |
Länge des längsten Pfades von Wurzel zu Blatt |
|
|
Baum - Niveau |
"Ebene" des Baums (0 indiziert) |
|
|
Baum - Member |
- parent (optional) - Data - LeftChild - RightChild |
|
|
Baum - Preorder A / \ B c |
output -> Left -> Right | A - B -C |
|
|
Baum - Inorder A / \ B c |
Left -> Output - Right |B - A - C |
|
|
Baum - PosterOrder A / \ B c |
Left -> Right -> Output | B - C - A |
|
|
Baum - LevelOrder A / \ B c |
Niveau n -> Niveau n+1 -> etc | A - B - C |
|
|
UPN |
PostOrder Traversal des Syntax-Trees <=> Stack [O1, 02, Operator] Eg.: 2 5 + = 2+5 = 7 |
|
|
Syntaxanalyse |
1. Lexikalische Analyse <-> Zerlegen in Tokesn 2. Syntax Analyse <-> Basierend auf Grammatik |
|
|
Backus - Naur Form |
"< ... > ::= <...> o <...> | <...> | 1 | 2 | 3 | ... " |
|
|
Endrekursion |
Funktion wird "auf dem Weg hoch" berechnet. Rekursiver Aufruf ist die Letzte Operation. <=> Schleife (Iterativ) |
|
|
Suchbaum |
Wurzel / \ Alle Elemente kleiner Alle Element größer * Inorder zählt sortierte Reihenfolge auf |
|
|
AVL Kriterium |
balance(T) := Höhe(TR) - Höhe(TL) balance(T) in {-1, 0, 1} für jeden Knoten |
|
|
AVL Baum |
Baum der das AVL-Balance Kriterium an jedem Knoten erfüllt balance(T) = Höhe(TR) - Höhe(TL) in {-1, 0, 1} |
|
|
Suchbaum :: Einfügen |
1. Erfolglose Suche - 'x' letzter besuchter Knoten 2. Erzeugen eines neuen Knotens und einfügen an x |
|
|
Suchbaum :: Löschen |
Y / \ X ... 1. Suche ; 2. { X ist Blatt -> Lösche X { X hat 1 Blatt -> Mache Y Parent des Blatts { X hat 2 Blätter -> ... |
|
|
Suchbaum :: Löschen (eines Knoten mit 2 Kinder) |
Lösche X & sei L & R linker / rechter Teilbaum Suche M - das Minimum in R Ersetze X durch M (remember Parent) Setzte L & R als linkes / Rechts Kind von M Aktualisiere Parent |
|
|
Einfache Links-Rotation |
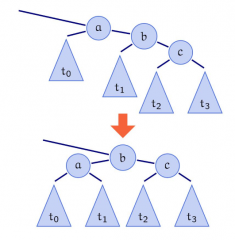
|
|
|
Einfache Rechts-Rotation |
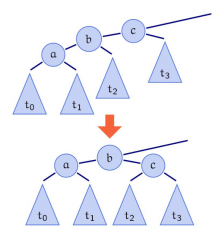
|
|
|
Doppel (Rechts-Links)-Rotation |
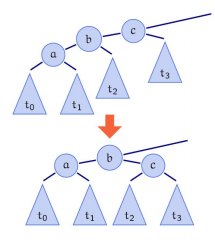
|
|
|
Doppel (Links-Rechts)-Rotation |
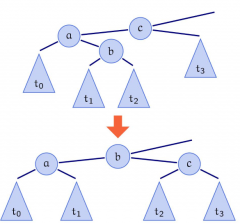
|
|
|
AVL-Baum :: Einfügen |
1. BST einfügen 2. Rekursiver Aufstieg bis zur Wurzel & AVL-Kriterium checken Verletzt => Rotation |
|
|
2-3-4 Baum |
2, 3, 4 Kinder pro Knoten (entsprechend 1,2,3 Schlüssel) |
|
|
2-3-4 Baum :: Split & Merge |
Split eines Knotens <=> 4 Kinder -> durch "hochziehen" des mittleren Knotens in den Parent-Knoten und dort "einsortieren" |
|
|
2-3-4 Baum :: Bottom-Up |
Einfügen in 1. 2,3 Knoten -> nur einfügen 2. 4 Knoten -> Split (hochziehen des mittleren Eintrags) + rekursiver Aufstieg solange parent-Knoten dadurch zu 4 knoten wurden -> Einfügen in neuen Blattknoten |
|
|
2-3-4 Baum :: Top-Down |
Beim Suchen (im Abstieg) teile alle besuchten 4 Knoten -> Einfügen in Blattknoten |
|
|
Rot-Schwarz-Baum - Intuition |
Binäre Baum in dem jeder Knoten rot oder schwarz gefärbt wird -> Stabilitätskriterium Es existiert eine bijektive Abbildung zwischen RS & 234 Bäumen |
|
|
Rot-Schwarz Baum - Definition |
1. Jeder Knoten ist rot oder schwarz 2. Wurzel ist schwarz 3. Alle Blätter sind schwarz (Dummies) 4. Beide Kinder eines roten Knotens sind schwarz 5. Jeder Pfad von einem Knoten zu allen erreichbaren Blättern enthält gleich viele schwarze Knoten |
|
|
Rot-Schwarz Baum :: Einfügen 1-2 |
Einzufügender Knoten (n) ist rot "()" (p parent, g grandparent, u uncle) 1. (n) ist wurzel -> umfärben zu n 2. p ist schwarz -> fertig 3-5. ... |
|
|
Rot-Schwarz Baum :: Einfügen 3-5 |
Einzufügender Knoten (n) ist rot "()" (p parent, g grandparent, u uncle) Fall "rot-rot" - (p)&(n) 1. u ist schwarz -> Restrukturieren 2. (u) ist rot -> umfärben + Rekursion aufwärts |
|
|
B Bäume |
"Große 234 Bäume" zur effizienten Speicherung im externen Speicher. Jeder Knoten hat zw. m+1 & 2m+1 Kinder - Wurzel hat mindestens 2 Kinder oder ist ein Blatt Alle Blätter liegen auf der gleichen Ebene |
|
|
B Bäume :: Einfügen |
1. Knoten mit < 2m Einträgen -> in Liste einsortieren 2. Knoten mit == 2m Einträge -> Einsortieren (2m+1 Einträge) -> Mittleren Knoten in Elternknoten -> Linke Hälfte bleibt -> Rechte Hälfte in neuen Knoten & an den neuen Zweig des mittleren Knoten hängen |
|
|
Splay Tree |
'Verschieben' von Einträgen beim Zugriff nach oben (Rotationen) => Häufig gebrauchte Einträge landen weiter oben |
|
|
Tries |
* Text Retrieval * Jede Kante "hängt" einen Buchstaben an das Wort an. * Jeder Knoten ist das Wort, gebildet aus der Zeichenkette von der Wurzel zum Knoten |
|
|
Heap (Min-Heap) Analog für Max-Heap |
Kinder eines Knoten sind größer Jeder Teilbaums eines Min-Heap ist ein Min-Heap => Kleinster Eintrag in der Wurzel -> Vollständiger Baum (bis auf letzte Ebene) -> implementiert als Feld |
|
|
Heap als Feld (1 Indiziert) |
Geg ein Knoten via Index (k) P = k//2 L = 2k R = 2k+1 |
|
|
Heap als Feld (0 indiziert) |
Geg ein Knoten via Index (k) P = (i-1)//2 L = 2i+1 R = 2i+2 |
|
|
Heapify :: UpHeap - Top Down |
Vergleiche Knoten mit Parent, wenn Knoten die Heap-Eigenschaft verletzt, tausche beide. |
|
|
Heap :: Einfügen |
Hänge Eintrag ans Array-Ende, "Upheape" es bis das Heap-Kriterium wieder erfüllt ist |
|
|
Heap :: Löschen des kleinsten Eintrages |
Tausche Wurzel mit letztem Eintrag, Lösche letzten Eintrag. Wenn Wurzel größer als das kleinere Kind, tausche. -> Rekursiv bis Element in Heap 'passt' |
|
|
Heapify :: DownHeap - Bottom Up |
Geg.: Ein Array. Beginne beim letzten Inneren Knoten (Parent vom Letzen Knoten) Teste Wurzel mit beiden Kindern, tausche wo nötig, decrement & continue |
|
|
HeapSort |
O(n log(n)) In Place Nicht Stabil Sortierreihenfolge via Min/Max-Heap |
|
|
Hashing |
Mittelwert von Space vs. Time Hashfunktion berechnet Hash-Wert des Objekts H: Obj -> [0, n], wird zum Indizieren der Tabelle verwendet |
|
|
Hashfunktion |
H: Obj -> [0, n] 1. Konsitent x = y -> H(x) = H(y) 2. Deterministisch Möglichst: - Effizient - Gleichverteilen Eg.: H(x) = x mod m (mit m in Prime) |
|
|
Kollisionsbehandlung |
Seperate Chaining Open Addressing - Lineares - Quadratisches - Double-Hashing |
|
|
Hashing :: Füllgrad |
a = n / m |
|
|
Seperate Chaining |
Array von Listen, Bei jeder Kollision wird in die Liste eingefügt - Wird ineffizient bei großem Füllgrad, funktioniert jedoch noch |
|
|
Lineares / Quadratisches Sondieren |
Wenn Hashwert in einem schon belegten Feld resultiert wird eine lineare (Quadratische) Folge von Zahlen addiert bis ein freier Platz gefunden wird (finden erfolgt Analog <-> Vorsicht beim Löschen) - Für Füllgrad > 1 "kaputt" |
|
|
Double Hashing |
Zweite Hashfunktion zum Bestimmen (Modifizieren) der Sprungweite im linearen Sondieren + Sprungweite ist so für fast jeden Eintrag anders - Zweite Hashfunktion darf nie 0 werden, sonst 'bricht' das lineare Sondieren (H(x) + i *0 = H(x)) |
|
|
(Un) Gerichtete Graphen (un) directed graph |
Kante A -> B ungleich Kante B -> A vs. Kante A <-> B |
|
|
Gewichtete vs Ungewichtet Graphen |
Kanten haben verschiedene vs alle die gleiche "Länge" / Gewicht |
|
|
Graph - Def |
Menge von Knoten V & |
|
|
Teilgraph |
Teilmenge der Knoten & Kantenmenge |
|
|
Grad (eines Knoten) |
Anzahl der eingehenden Kanten In digraphs: Unterteilung in indegree & outdegree |
|
|
Pfad |
Folge von (durch Kanten verbundenen) Knoten, wenn alle Knoten verschieden sind. |
|
|
Zyklus |
Folge von (durch Kanten verbundenen) Knoten,
wenn Knoten wiederholt vorkommen. Aka alles was kein Pfad ist |
|
|
Azyklisch |
Graph ohne Zyklen |
|
|
DAG |
directed acyclic graph (Gerichteter Zyklenfreier Graph) |
|
|
Ajazenzmatrix |
n-te Zeile - ausgehende Kanten des n.ten Knotens n-te Spalte - eingehende Kanten des n.ten Knotens |
|
|
Kantenliste |
edgelist = {Anzahl der Knoten, Anzahl der Kanten, Startknoten, Endknoten (*)} (*) jeder Kante Eg.: {6, 11, 1,2, 1,3, 1,4 ... } |
|
|
Knotenliste |
nodelist = {Anzahl Knoten, Anzahl Kanten, Valenz eines Knotens, Nachbarschaft eines Knotens (*) } (*) Für jeden Knoten {6, 11, 2, 2,3, 0, 3, 1,4,6, ... } |
|
|
Knotentabelle |
Zwei Listen 1. Ausgehende Kanten 1ring={2,3, 1,4,6, 1, 3,5 } 2. Indizes Speichert ab welchem (& bis zu welchem) Index die Elemente aus der 1ring-liste zum aktuellen Knoten gehören E.g.: {0, 2, 2, 5, ... } |
|
|
Heuristiken (Eigenschaften) |
- Dürfen nicht unterschätzen - Schnell berechenbar |
|
|
Maximaler Fluss |
|
|
|
Graph :: Quelle |
Nur ausgehende, keine eingehenden Kanten |
|
|
Graph :: Senke |
Nur eingehende, keine ausgehenden Kanten |
|
|
Maximaler Fluss (Def) |
1. Kapazitätsberschränkung
- Fluss durch eine Kante <= Kapazität der Kante 2. Antisymmetrie - Fluss von i nach j = Negativer Fluss von j nach i f(u, v) = -f(v, u) 3. Flusserhaltung - Der in einen Knoten gelangende Fluss = der den Knoten verlassende Fluss |
|
|
Max Flow <-> Min Cut |
Der Wert des maximalen Flusses in einem Graphen ist gleich den Kosten des minimalen Schnitts |

